Next post Previous post

Physics and units again

March 12, 2023 at 2:54 PM by Dr. Drang

I don’t want this place to turn into a Matt Parker followup blog, but there are things in his recent Pi Day video that fit in with comments I made on his Runge video, specifically the part about engineers embedding unit conversions within formulas. So go ahead and watch the video if you haven’t already.

The formula of interest is the one used to calculate the speed of a car during a turning skid:

v=15rfv = \sqrt{15\: r f}

where r is the radius of the car’s motion during the skid, in feet, and f is the dynamic coefficient of friction between the tires and the road. The left-hand-side, v, is the speed of the car in miles per hour.

Traffic accident reconstructionists, like Matt’s guide Eric in the video, are able to use this formula because they can measure the radius of the skidmark on the pavement and can either measure the friction coefficient directly, as they do in the video, or just estimate it from known values. As you can see in the video, Eric expected the value to be 0.7, and they measured it as 0.68.

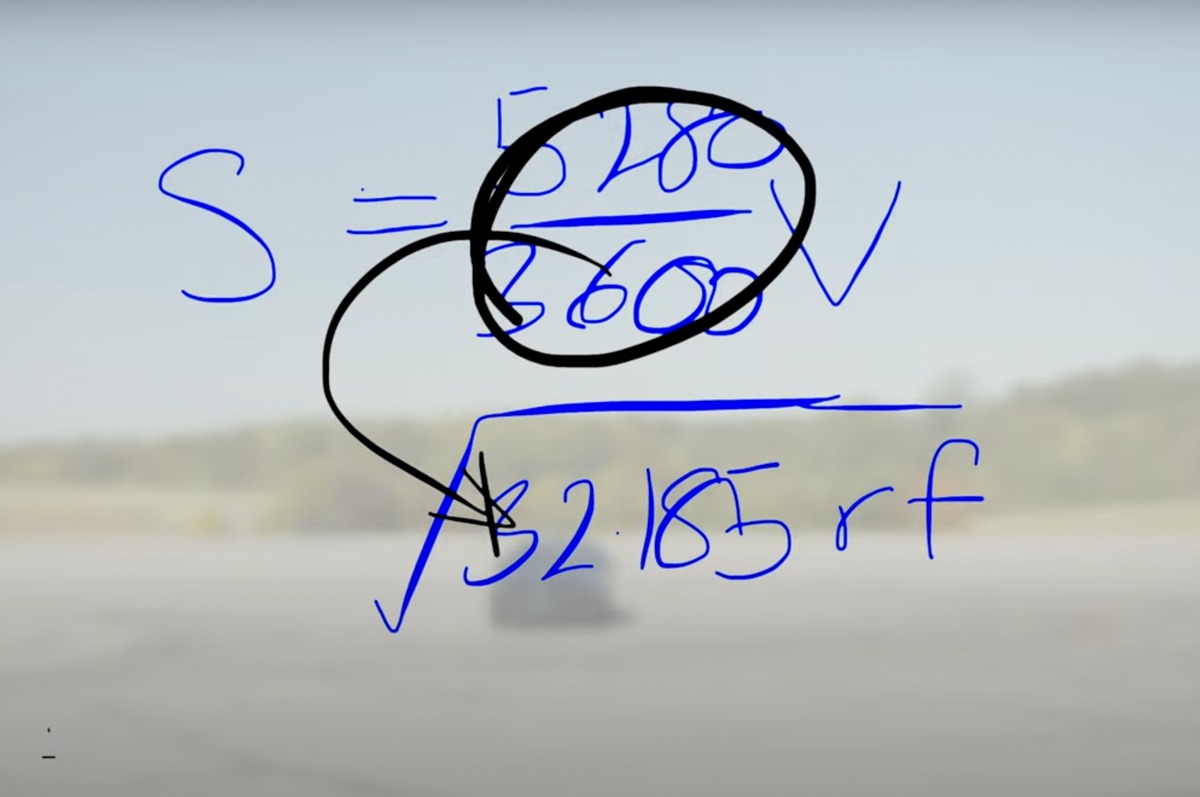
The 15 in the formula is not a pure number, it’s a combination of the acceleration due to gravity, g, and a conversion from feet per second to miles per hour. The pure mechanics version of the formula is

v=grfv = \sqrt{g r f}

which Matt derives in the video. Here in the US, we would measure r in feet and use a g of 32.2ft/s232.2 \: \mathrm{ft/s^2}. That gives us a v in feet per second, which isn’t how vehicle speeds are typically presented. To get the speed in miles per hour, we need to convert feet to miles and seconds to hours, which is done like this:

v=(32.2ft/s2)rf(1mile5280t)(3600s1hr)v = \sqrt{(32.2 \: \mathrm{ft/s^2})\: r f} \left( \frac{1 \: \mathrm{mile}}{5280 \: \mathrm{t}} \right) \left( \frac{3600 \: \mathrm{s}}{1 \: \mathrm{hr}} \right)

Since 3600/5280=0.6823600/5280 = 0.682, we can bring the conversion fraction inside the square root like this,

v=(32.2)(0.682)2rf=14.97rfv = \sqrt{ (32.2)(0.682)^2\: r f } = \sqrt{ 14.97\: r f }

and 15 is close enough to 14.97 justify the substitution. The 15 is the acceleration due to gravity in these rather weird units:

mile2ft·hr2\mathrm{\frac{{mile}^2}{{ft} \cdot {hr}^2}}

Brief aside
You may have noticed that Matt wrote the conversion fraction upside-down in the video.

Conversion equation with error

It’s the sort of thing you do when you’re in a hurry.

If you’re an American, you might be wondering why he’s using 32.185ft/s232.185 \: \mathrm{ft/s^2} for g. It’s an overly precise conversion from the usual SI value for g: 9.81m/s29.81 \: \mathrm{m/s^2}.

9.81ms2(1in0.0254m)(1ft12in)\mathrm{9.81 \: \frac{m}{s^2}} \left( \mathrm{\frac{1\: in}{0.0254\: m}} \right) \left( \mathrm{\frac{1\: ft}{12\: in}} \right)

The 0.0254 and the 12 are exact numbers, but the 9.81 isn’t. Three digits is all that’s justified, which is why we use 32.2ft/s232.2 \: \mathrm{ft/s^2}.

Although I do accident reconstruction professionally, I’ve never delved much into traffic accident reconstruction. But when I have, I’ve noticed that the formulas reconstructionists use are often in this form, where the formula includes a hidden unit conversion and only works if the inputs and outputs are in a particular set of units. When I saw this video, I realized I could have used one of these formulas in my discussion last month of formulas with embedded units.

(I also thought of a friend of mine who passed away last year. He always said the hardest part of traffic accident reconstruction was the back-and-forth conversion between feet per second and miles per hour.)

By the way, no one I know uses 5280 and 3600 to convert between fps and mph. They always use 88 and 60 because

88fts(1mile5280ft)(3600s1hr)=60milehr88\: \mathrm{\frac{ft}{s}} \left( \mathrm{\frac{1\: mile}{5280 \: ft}} \right) \left( \mathrm{\frac{3600 \: s}{1 \: hr}} \right) = 60\: \mathrm{\frac{mile}{hr}}

Of course, you could reduce the fraction further and say that 22 fps is 15 mph, but 60 mph is such a useful speed (a mile a minute) that people usually remember the conversion that way.

One last thing: Matt makes a small disparaging comment about having to use US customary units in the video, but even if he were working in metric, I’m pretty sure he’d have to do a unit conversion. Car speeds in the more enlightened parts of the world are typically given in kilometers per hour, not meters per second.

v=(9.81m/s2)rf(1km1000m)(3600s1hr)=127rfv = \sqrt{ (9.81 \: \mathrm{m/s^2})\: r f} \left( \mathrm{\frac{1\: km}{1000\: m}} \right) \left( \mathrm{\frac{3600\: s}{1\: hr}} \right) = \sqrt{127\: r f}

You could probably use 130 without much worry. After all, you’re going to reduce the error in v when you take the square root.

Next post Previous post