Next post Previous post

Doppler Petty

July 7, 2023 at 10:25 AM by Dr. Drang

A couple of days ago, as I was out taking my morning walk, I passed a guy on a bicycle who was coming the opposite way down the path. I was northbound, he was southbound. He was, annoyingly, playing his music out loud through a speaker instead of privately through earbuds. Less annoyingly, the music he was playing at the time of our encounter was Tom Petty’s “Free Fallin’,” and the point at which we passed was when Tom was belting out “Now I’m freeeeeeeeeeeeeee….” What the Doppler effect did to his voice was pretty funny.

As I continued the walk, I wondered if I could calculate the drop in pitch. The answer was yes, but not in my head. The algebra isn’t especially hard, but terms kept disappearing as I tried to manipulate back and forth between wavelength and frequency. I blame the dog I was walking for distracting me.

When I got home, I scratched out a solution. My assumptions were:

Before we start plugging in numbers, let’s figure out the formulas we need to use. We’ll call the speed of sound cc, my northbound speed vpv_p, the bike’s southbound speed vbv_b, and the frequency of the note f0f_0. For each cycle of the note, the bike moves south a distance

vbf0\frac{v_b}{f_0}

which means the sound waves south of the bike are squeezed together by this much and the sound waves north of the bike are stretched out by this much. If the bike weren’t moving, the wavelength of the note would be

λ0=cf0\lambda_0 = \frac{c}{f_0}

so the wavelength south of the bike is

λ0−vbf0=c−vbf0\lambda_0 - \frac{v_b}{f_0} = \frac{c - v_b}{f_0}

and the wavelength north of the bike is

λ0+vbf0=c+vbf0\lambda_0 + \frac{v_b}{f_0} = \frac{c + v_b}{f_0}

A stationary person south of the bike would therefore hear the note at a frequency of

cc−vbf0=cc−vbf0\frac{c}{\frac{c - v_b}{f_0}} = \frac{c}{c - v_b}\, f_0

and a stationary person north of the bike would hear the note at a frequency of

cc+vbf0=cc+vbf0\frac{c}{\frac{c + v_b}{f_0}} = \frac{c}{c + v_b}\, f_0

But I wasn’t stationary. I was moving north at vpv_p, so when the bike was still north of me, I was encountering the sound waves faster than a stationary person would. They were passing me at a frequency of

c+vpc−vbf0\frac{c + v_p}{c - v_b}\, f_0

And after the bike had passed, the sound waves were passing me at a rate slower than they would pass a stationary person,

c−vpc+vbf0\frac{c - v_p}{c + v_b}\, f_0

The difference between these frequencies, which is the drop in pitch as perceived by me as the bike passes is

c+vpc−vbf0−c−vpc+vbf0=2cc2−vb2(vb+vp)f0\frac{c + v_p}{c - v_b}\, f_0 - \frac{c - v_p}{c + v_b}\, f_0 = 2 \frac{c}{c^2 - v_b^2} (v_b + v_p) \, f_0

Plugging in the assumed values—after converting the speed of the bike and me into feet per second—we get a drop in frequency of

35.21Hz35.21\; \mathrm{Hz}

In this frequency neighborhood, a semitone is about

880Hz(212−1)=52.3Hz880 \; \mathrm{Hz} \left( \sqrt[12]{2} - 1 \right) = 52.3 \; \mathrm{Hz}

so what I heard was something less than a semitone of warble as the bike passed me. I would’ve guessed at least a semitone, but I’m not very musical.

You may have noticed that the formula for the drop in pitch,

2cc2−vb2(vb+vp)f02\, \frac{c}{c^2 - v_b^2} (v_b + v_p) \, f_0

includes a term in which we’re doing a subtraction of values, c2c^2 and vb2v_b^2, that are orders of magnitude apart. It could be approximated by

2vb+vpcf02 \, \frac{v_b + v_p}{c}\, f_0

with very little error. Using our values, the approximate pitch drop is 35.20 Hz, which is certainly close enough to result using the exact formula.

I should mention that after I derived the equations above, I pulled out my father’s old copy (2nd edition, 1955) of Sears and Zemansky’s University Physics. It confirmed my equations and also included this nice sketch showing how the wavelengths expand and contract on different sides of the moving sound source. They’re using uu for the speed of sound and vSv_S and vLv_L for the speeds of the speaker and listener. Each non-concentric circle represents one cycle.

Doppler wave figure from Sears and Zemansky

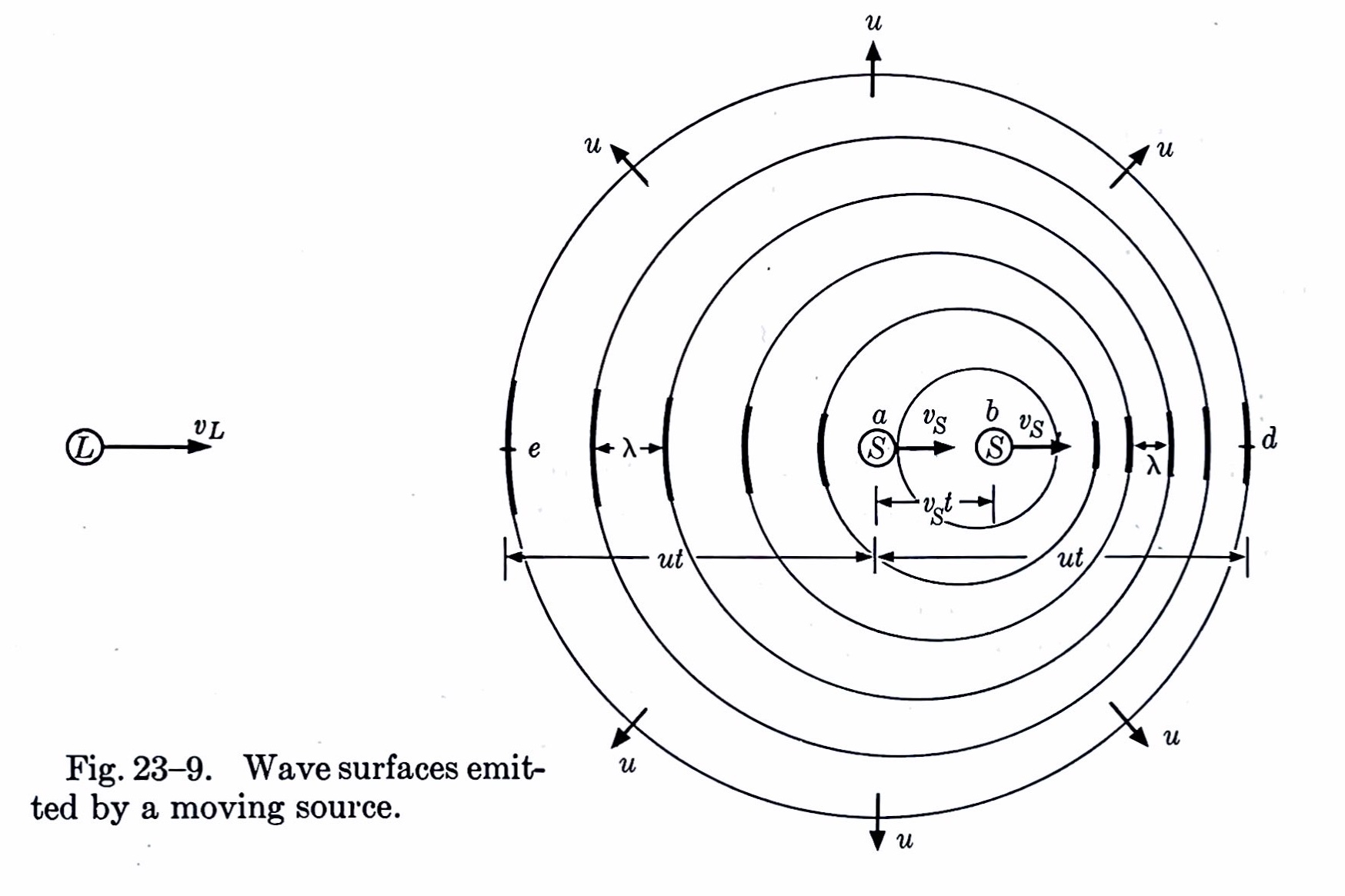
University Physics is one of those books that has achieved so much fame and been through so many editions that its original authors are present only through absorption into the title. Marks’ Standard Handbook for Mechanical Engineers and Roark’s Formulas for Stress and Strain are other examples that come to mind.

Next post Previous post