Weekdays with Pope Gregory
October 9, 2023 at 9:03 PM by Dr. Drang
Yesterday, longtime friend of the blog Nathan Grigg posted this on Mastodon:
Did you know that October 8 is 3.5% less likely to fall on a Sunday than a Saturday? Enjoy your rare day!
It’s been a while since I’ve done any calendrical calculations of note, so I decided to confirm Nathan’s numbers (I had no doubt he was correct). And since I’ve never done anything like this in Mathematica, it seemed like a good opportunity to learn how it handles dates.
Mathematica’s date object is most easily created using the cleverly named DateObject function. Yesterday was
DateObject[{2023, 10, 8}]
where the argument is the year-month-day list for the date of interest. To get the day of the week, we can wrap this in DayName,
DayName[DateObject[{2023, 10, 8}]]
which will return Sunday. This, like the other days of the week, is not a string, but a Mathematica object of its own. Another way to express the day of the week, which will turn out to be more convenient for this problem, is numerically, via the ISOWeekDay property of the DateValue function:
DateValue[DateObject[{2023, 10, 8}], "ISOWeekDay"]
This returns 7, because ISOWeekDay is defined as 1 for Monday through 7 for Sunday.
With this in hand, I did a brute force solution. The Gregorian calendar we use repeats itself every 400 years, so I generated a table of 400 values for the weekday number of October 8 from 1800 through 2199. The command was
gregCycle = Table[DateValue[DateObject[{y, 10, 8}], "ISOWeekDay"], {y, 1800, 2199}]
and the output was this list, which I’ve reformatted for easier reading:
3 4 5 6 1 2 3 4 6 7 1 2 4 5 6 7 2 3 4 5
7 1 2 3 5 6 7 1 3 4 5 6 1 2 3 4 6 7 1 2
4 5 6 7 2 3 4 5 7 1 2 3 5 6 7 1 3 4 5 6
1 2 3 4 6 7 1 2 4 5 6 7 2 3 4 5 7 1 2 3
5 6 7 1 3 4 5 6 1 2 3 4 6 7 1 2 4 5 6 7
1 2 3 4 6 7 1 2 4 5 6 7 2 3 4 5 7 1 2 3
5 6 7 1 3 4 5 6 1 2 3 4 6 7 1 2 4 5 6 7
2 3 4 5 7 1 2 3 5 6 7 1 3 4 5 6 1 2 3 4
6 7 1 2 4 5 6 7 2 3 4 5 7 1 2 3 5 6 7 1
3 4 5 6 1 2 3 4 6 7 1 2 4 5 6 7 2 3 4 5
7 1 2 3 5 6 7 1 3 4 5 6 1 2 3 4 6 7 1 2
4 5 6 7 2 3 4 5 7 1 2 3 5 6 7 1 3 4 5 6
1 2 3 4 6 7 1 2 4 5 6 7 2 3 4 5 7 1 2 3
5 6 7 1 3 4 5 6 1 2 3 4 6 7 1 2 4 5 6 7
2 3 4 5 7 1 2 3 5 6 7 1 3 4 5 6 1 2 3 4
5 6 7 1 3 4 5 6 1 2 3 4 6 7 1 2 4 5 6 7
2 3 4 5 7 1 2 3 5 6 7 1 3 4 5 6 1 2 3 4
6 7 1 2 4 5 6 7 2 3 4 5 7 1 2 3 5 6 7 1
3 4 5 6 1 2 3 4 6 7 1 2 4 5 6 7 2 3 4 5
7 1 2 3 5 6 7 1 3 4 5 6 1 2 3 4 6 7 1 2
The choice of 1800–2199 was arbitrary—any 400-year stretch would have worked just as well.
I then generated a histogram from these values using
Histogram[gregCycle]
which returned this plot:
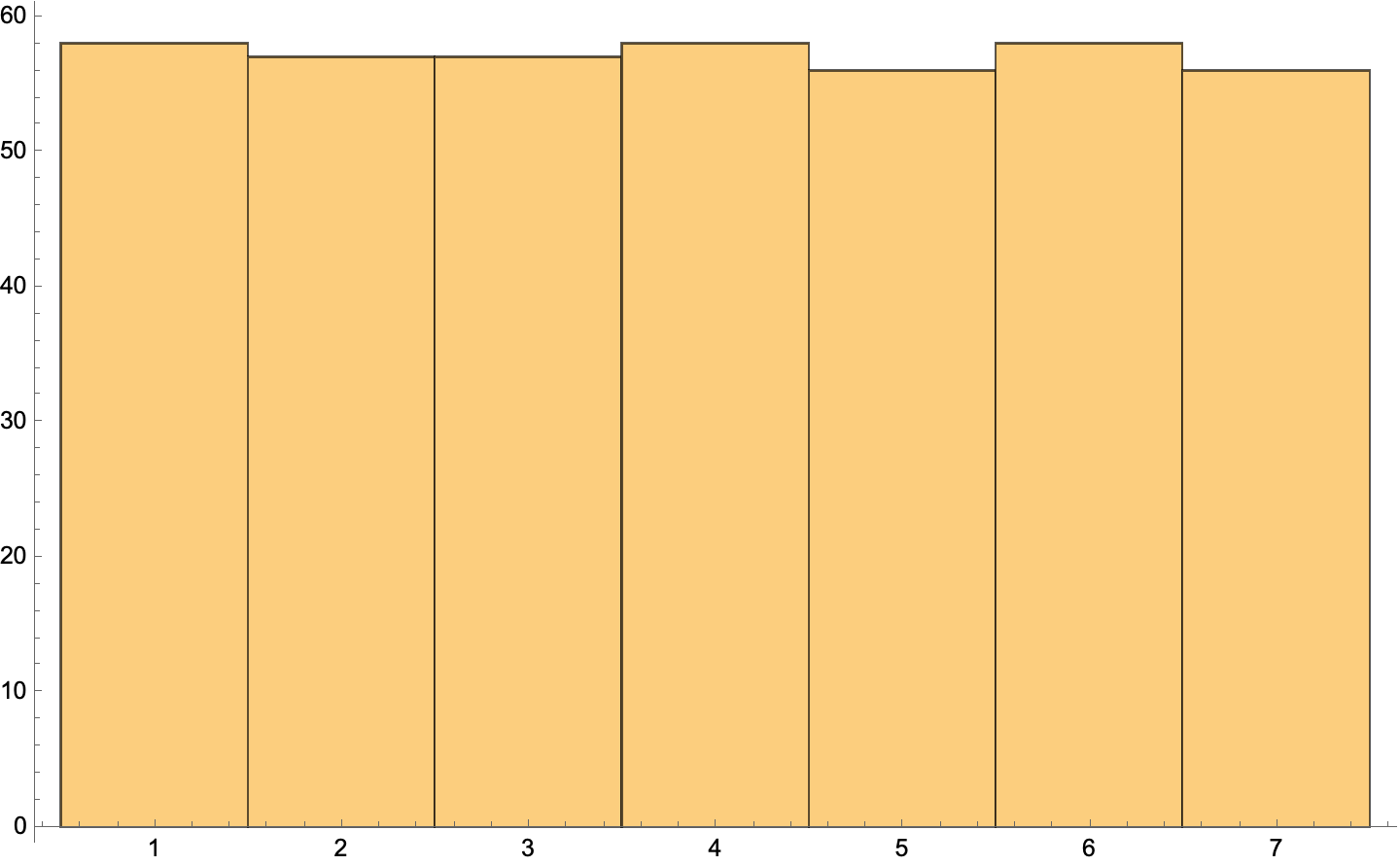
When you’re working in the Mathematica app, you can hover over each column to see a popup of the count for that weekday. Or you can run this,
KeySort[Counts[gregCycle]]
to get the heights of all the columns at once
<|1 -> 58, 2 -> 57, 3 -> 57, 4 -> 58, 5 -> 56, 6 -> 58, 7 -> 56|>
(The weird-looking brackets and the arrows are how Mathematica formats associations, which are the equivalent of dictionaries in Python and hashes in Perl.)
As you can see, there are 56 Sundays and 58 Saturdays per cycle, so Sundays are 3.5% (OK, 3.44828…%) less common than Saturdays, just as Nathan said.
That the weekdays aren’t uniformly distributed comes from the cycle length of the Gregorian calendar. 400 is not a multiple of 7, so it’s impossible for the all the weekdays to occur the same number of times in 400 years. Still, it does seem a little weird—to me, anyway—that the counts differ by as much as two instead of just one.
You may object to this analysis. What’s the point of looking over a 400-year cycle when I’m only going to experience a fraction of it? Good point. More important, most (likely all) of us will never experience a century year that isn’t a leap year. We’re living in this two-century stretch of time that might just as well be governed by the Julian calendar—a leap year every fourth year with no exceptions. Such a calendar repeats every 28 years, not every 400, and because 28 is a multiple of 7, October 8 falls on every weekday an equal number of times each cycle. Whether you personally will experience an equal number of October 8ths on a Sunday as on a Saturday will depend entirely on where in the cycle you were born and where in the cycle you will die.
And on that happy note, we’ll close out this post.

