Structural continuity and the Francis Scott Key Bridge
April 1, 2024 at 5:06 PM by Dr. Drang
I don’t have anything particularly insightful to say about the collapse last week of the Francis Scott Key Bridge in Baltimore. But while reading some of the early reports on the collapse, I noticed two seemingly contradictory comments on the role of structural continuity in the bridge’s behavior, and I wanted to talk about them.
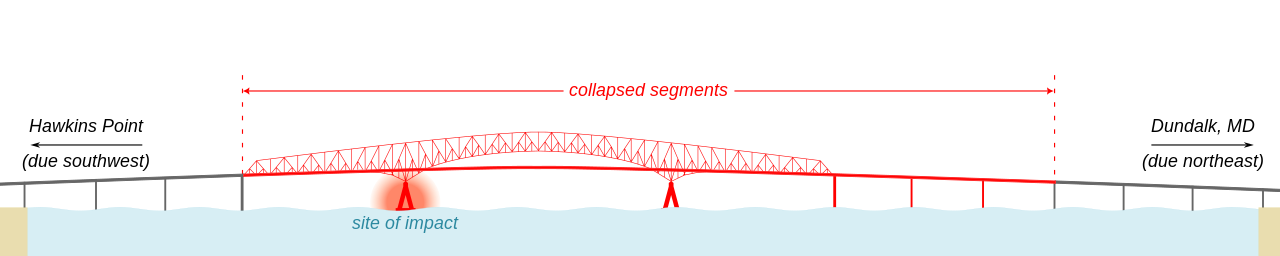
Image from Fvasconcellos on Wikipedia
The first is from this Wired article, which was pointed out to me by Leon Cowle:
“It’s a dreadful tragedy and something you hope never to see,” says David Knight, a bridge expert and specialist adviser to the UK’s Institution of Civil Engineers. But commenting on footage of the bridge collapse, he says he is not surprised by the manner in which it crumpled.
Large steel structures may seem invulnerable, but steel, explains Knight, is relatively lightweight for its size. As soon as it is pushed or pulled the wrong way with enough force, it can fold like paper. In this case, the Francis Scott Key Bridge was a “continuous,” or unjointed, bridge that had a 366-meter-long central truss section. (Truss bridges use steel beams, arranged in triangular shapes, to support their load.) The central truss was made up of three horizontal stretches, known as spans, with two sets of supports holding these above the water. It was the third-largest structure of its kind in the world.
“When you take a support away, there is very little in the way of robustness,” says Knight. “It will drag down, as we saw, all three spans.” The separate approach spans remain standing.
To start with, I doubt very much that anyone old enough to remember September 11, 2001, thinks that large steel structures are invulnerable, but let’s put that aside. The impression I got from reading this is that Knight thinks continuity contributed to the collapse, that it allowed the bridge to drag itself down once one of the interior supports was taken out by the ship.1
Another view on structural continuity came from Abieyuwa Aghayere, a professor in the Civil, Architectural and Environmental Engineering department at Drexel University, in this interview with WPVI in Philadelphia:
Aghayere analyzes structural collapses. He was surprised that this type of bridge, known as a continuous truss bridge, completely failed.
“When something is continuous, it is supposed to at least hang on,” he said. “What I saw was that once the pier that was supporting that span gave way, the bridge just went down. There was no hesitation.”
Aghayere thinks continuity is good and that it typically allows a structure to withstand damage.
So we have two experts who seem to have opposite ideas about the value of continuity. Who’s right?
First, let’s look at what continuity is and how it affect the behavior of structures in general. We’ll start with an elementary structure that has some of the continuity of the Key Bridge.2
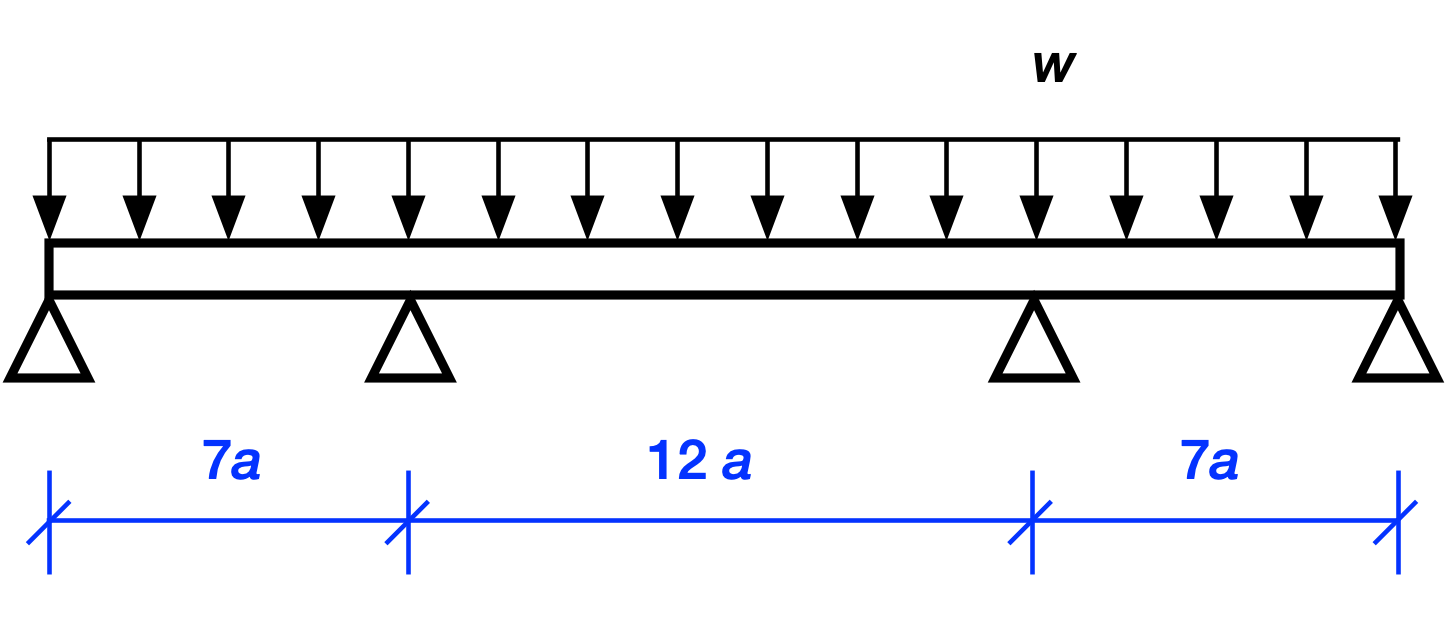
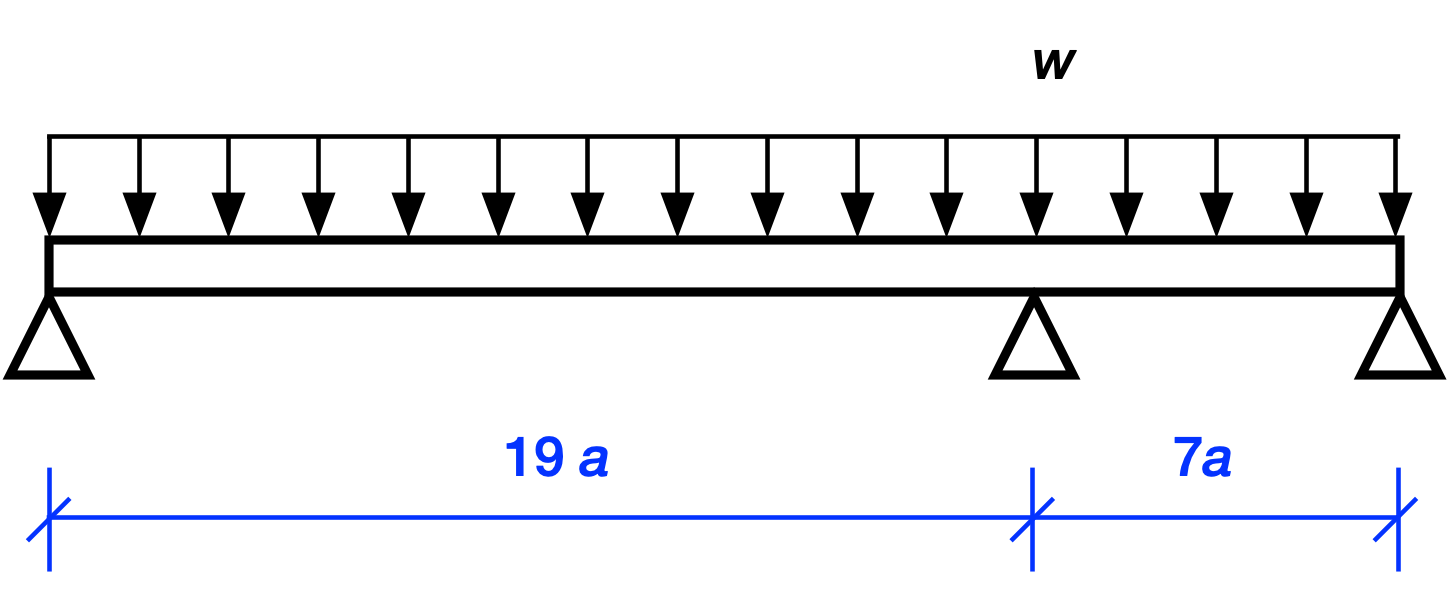
This is a three-span continuous beam of length 26a with a uniform load of intensity w applied to it (a has units of length and w has units of force per length). The three spans have lengths in the ratio 7:12:7 because the Key Bridge’s spans are about 700, 1200, and 700 feet. The beam is one long piece running from the left support to the right, with no joints in between. This is what’s meant by “continuous.”
Lots of three-span bridges, especially when the spans are short, are made with joints at the two interior supports because they’re easy to construct that way. Schematically, we’d draw such a bridge like this:
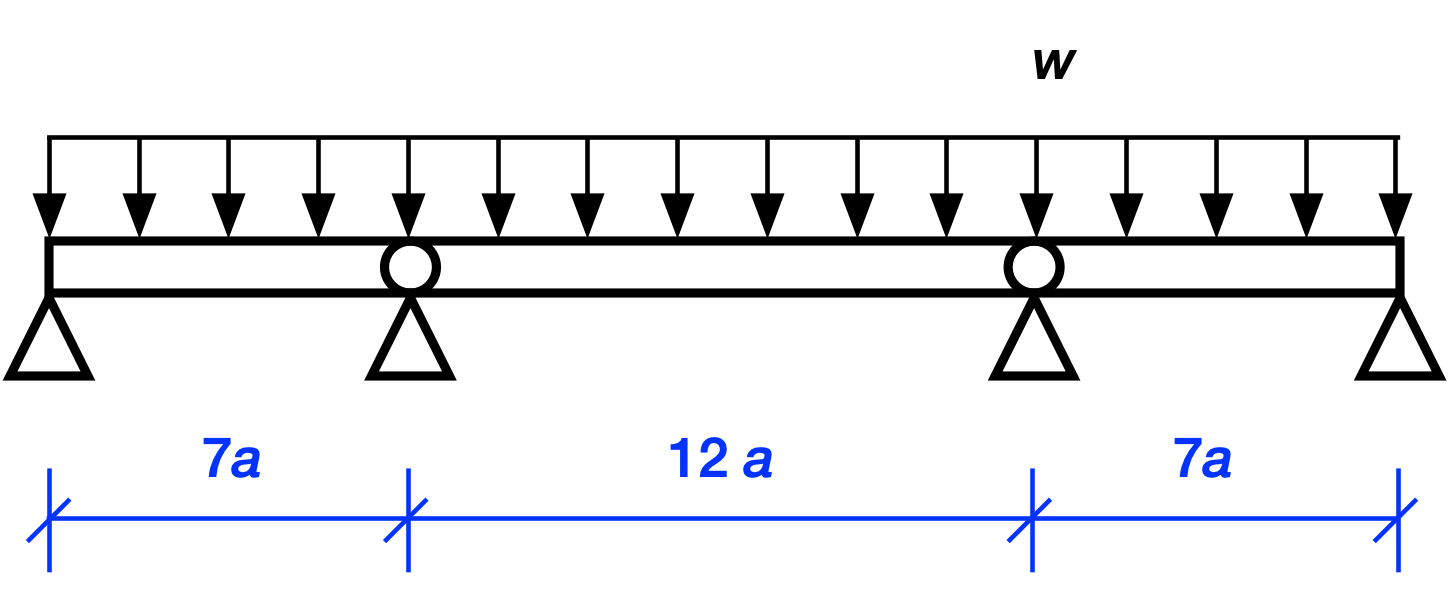
There aren’t really hinges at the interior supports, but we draw it that way to indicate that the connections at those locations are rotationally flexible—they don’t transfer much bending moment from one span to the next. The result is a structure that acts like three simple spans, one after the other.
Bending moments are proportional to the stresses in a structure, and structural engineering students spend a good chunk of their time learning how to calculate moments and draw moment diagrams. Here’s the moment diagram for the bridge with hinges at the supports:
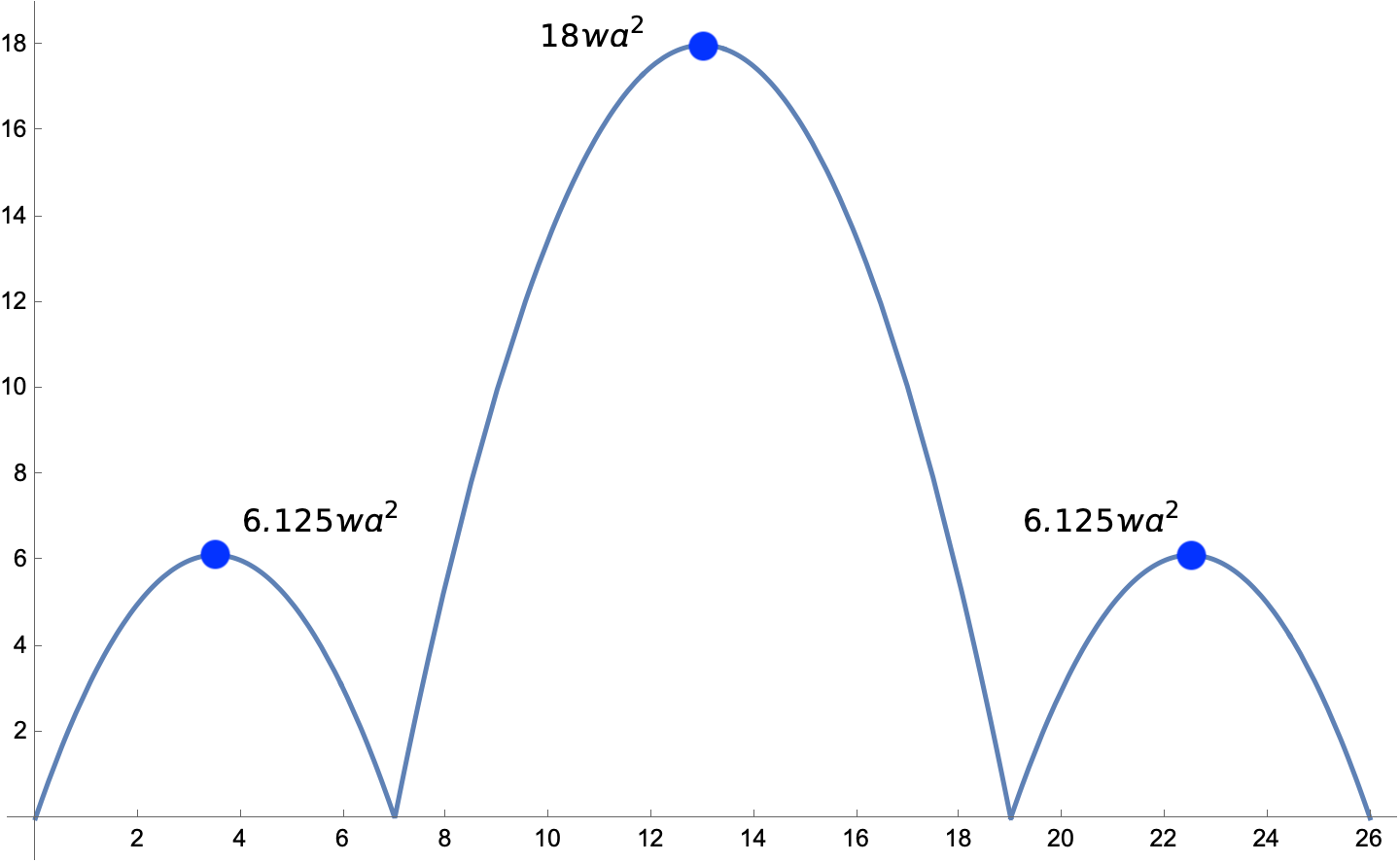
Note that has units of force per length times length squared, which works out to force times length, as expected for a moment.
For the continuous beam, the moment diagram is this:
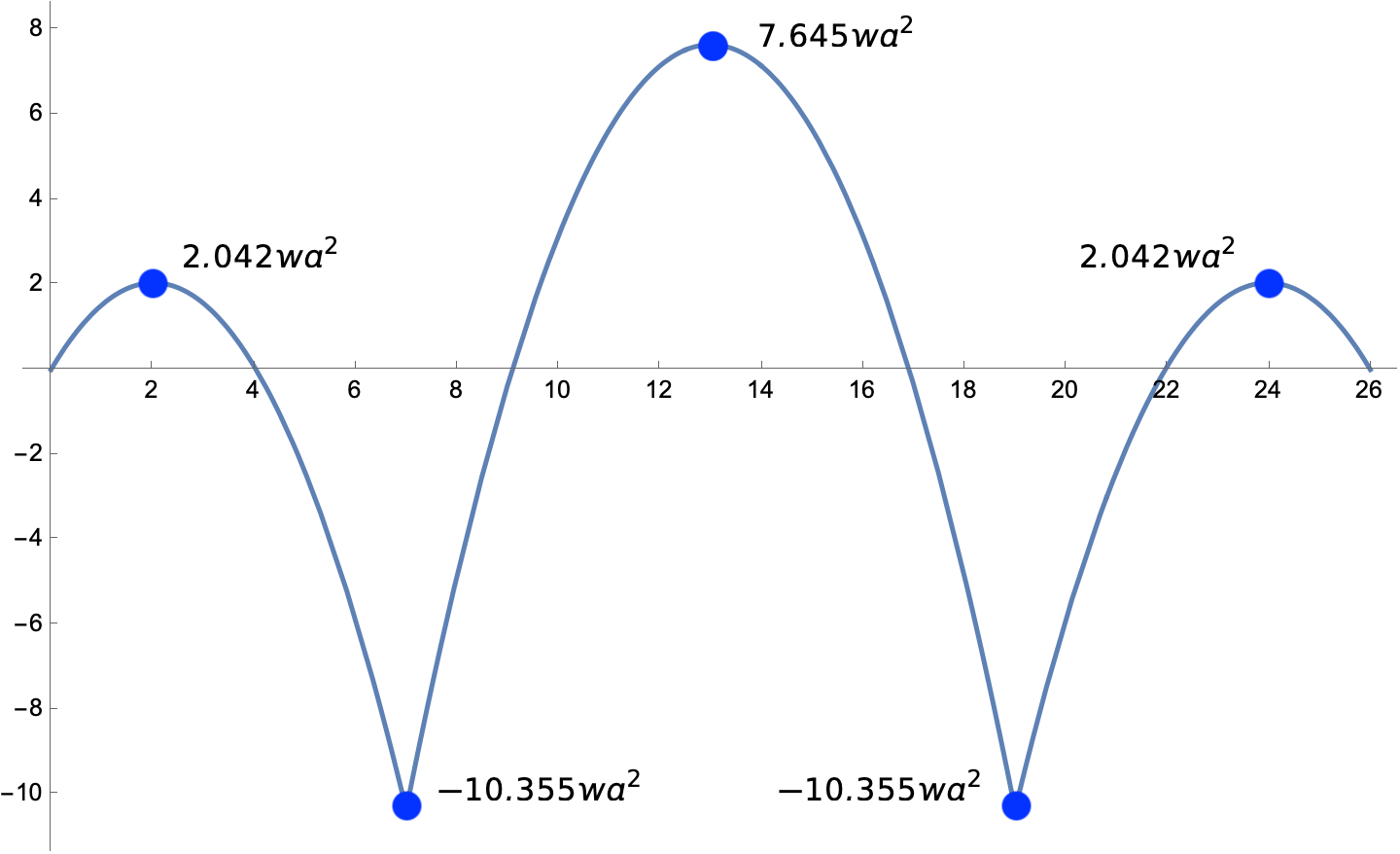
This shows the value of continuity. By making the bridge act like one long beam instead of three shorter beams, the peak moment in the structure has been reduced by almost half. Therefore we can reduce the stresses by almost half if we make the bridge continuous across the supports.
As a practical matter, though, we wouldn’t use the same beams if we changed the design from three simple spans to a continuous structure. We’d take advantage of the lower moments to give the continuous beam a smaller cross section, saving material and cost.
This isn’t to say that all structures should be made continuous. Providing continuity often involves greater building costs because of increased labor and the need for more or specialized construction equipment. There are always tradeoffs to be made. In the Francis Scott Key Bridge itself, the approach spans on either side of the three spans that collapsed look to be simple spans. Apparently, their shorter length—about 300 feet—didn’t create bending moments that justified the additional construction complexity that comes with continuity.
Now let’s look at what happens when we lose one of the interior supports. We’re not going to consider the forces involved in the impact itself, we’ll just assume the support magically disappeared.
If our structure is made of three simple spans, removing an interior support turns it into a mechanism, and the two spans that were propped up by the now-missing support fall down. There are no calculations to be done; two spans are lost but the other survives.
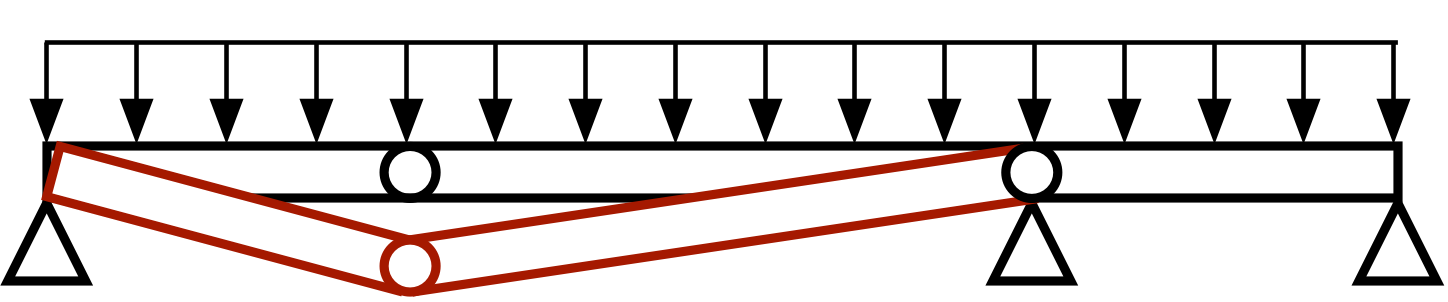
Because of the joint at the right interior support, the right span survives the loss of the left interior support. The left two spans don’t drag it down with them. This is a point in favor of the “continuity is bad” argument, but I don’t think it’s strong enough to win out over the continuity advantage we showed above. After all, if we didn’t design with continuity, the central span would have to be considerably larger, and it would still end up in the river.
If our structure is continuous, removing an interior support leaves us with a two-span continuous beam that looks like this:
This is not a mechanism and would not necessarily fall into the river, a point in favor of the “continuity is good” argument. But let’s look at the moment diagram for this structure.
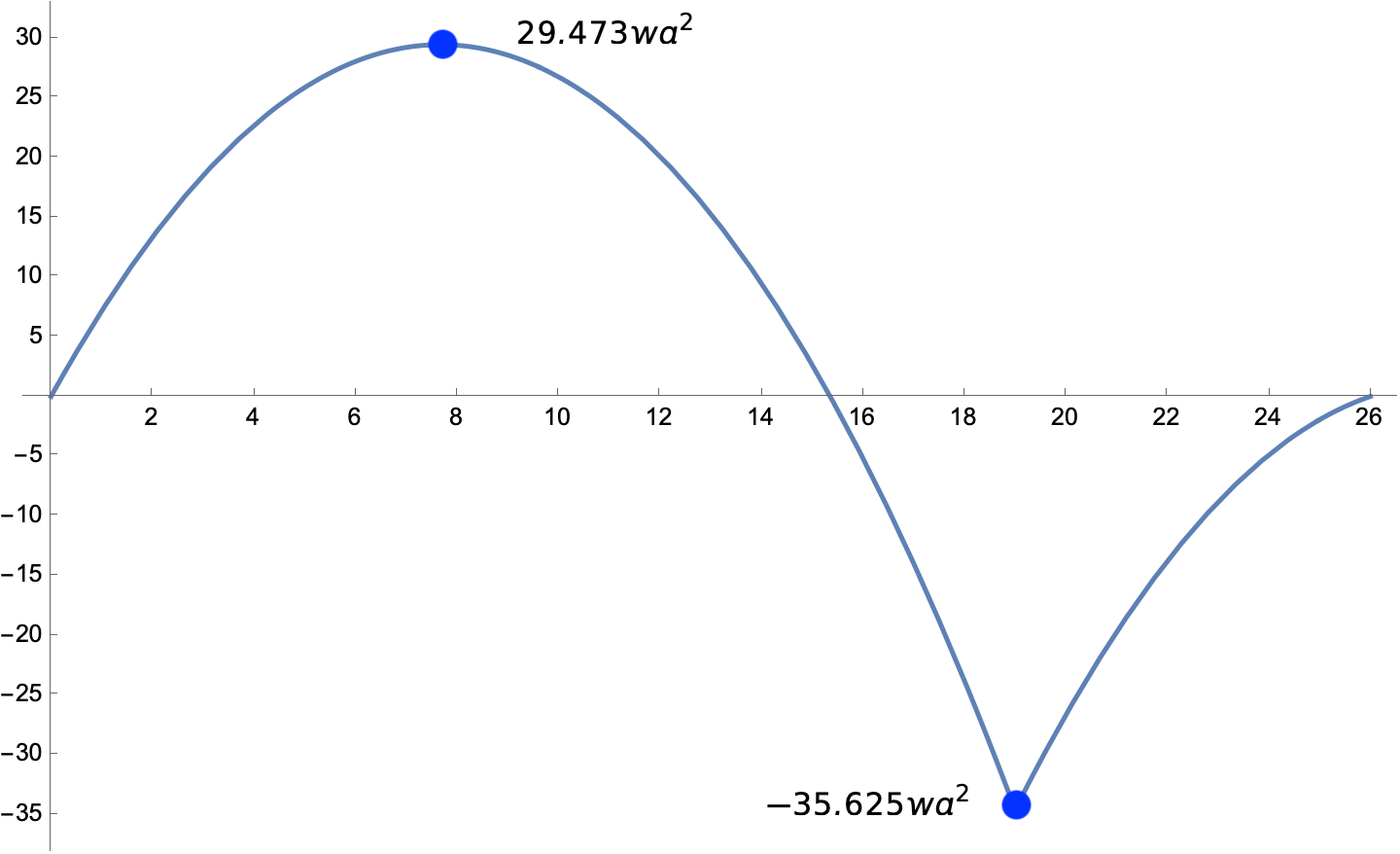
The peak moments are now over three times what they were before the support was removed. So while it’s conceivable that the bridge would stay up, the likelihood that it would do so is low.
Dr. Aghayere’s comment that continuity should allow a structure to “at least hang on” reminded me of something I learned in a structural reliability class over 40 years ago. Another student of my thesis advisor, a guy who was a few years ahead of me on the path to his Ph.D., had done a study of the reliability of continuous structures under different modes and sequences of failure. He learned that under typical design codes, the redundancy3 provided by continuity often doesn’t do much to increase the structure’s overall reliability. That’s because, as we talked about earlier, designers typically take advantage of continuity to reduce the cross sections of their structure’s components. The upshot is that failure in a particular location tends to lead to another failure elsewhere in the structure. In the case of the Key Bridge, it only took a couple more failures after the loss of the pier to bring the rest of the bridge down.
In short, while Mr. Knight’s and Dr. Aghayere’s comments on continuity are correct in theory, they aren’t very helpful in practice. No one would have designed the Francis Scott Key Bridge without taking advantage of continuity. Even if they hadn’t, the main span would still be blocking ship traffic and would be a bigger mess to clean up. And although continuous structures can survive the loss of some components, it’s very unlikely that long spans like this can survive the loss of an interior support.
The key to keeping bridges up over navigable waters is to build independent protective structures near—but not too near—the piers. The protective structures can get damaged by impact as long as they don’t transfer the load into the pier they’re meant to protect (that’s the “independent” part). Dr. Aghayere questioned the lack of protective structures in his interview, and he got that part exactly right.
-
This impression may have as much to do with how the author of the piece, Chris Baraniuk, presented Knight’s words. ↩
-
Please note, this is not meant to model even most of the structural features of the Key Bridge. For one thing, the center span isn’t arched. ↩
-
Redundancy is a reliability term having to do with the ability of a system to survive the failure of one or more of its components. ↩

