Next post Previous post

More than 100% pregnant

May 9, 2024 at 11:21 PM by Dr. Drang

Kieran Healy tweeted out a gem earlier this evening:

Yes, Professor Huberman, a probability of 120% is indeed “a different thing altogether.”1

While I find it fascinating that someone can run through an argument that clearly proves they are wrong and continue along as if they hadn’t, I don’t have any expertise in psychology, so I won’t try to explain it.

I do, however, have some expertise in probability, and Huberman is dancing around the edge of one of my favorite problems: If there’s a 1 in n chance of something happening in one try, what’s the probability of it happening in n tries?

Remarkably, the answer is not

n(1n)=1

It’s

1−(1−1n) n

The term in the parentheses is the probability of it not happening in a single trial. That term raised to the nth power is the probability of it not happening in n trials (assuming independence between trials). And subtracting that from 1 gives us the probability of it happening (at least once) in n trials.

What’s great about this problem is that you can make a pretty decent estimate of the answer without doing any calculations. The reason is

lim n→∞(1−1n) n=1e≈0.37

and so

lim n→∞1−(1−1n) n=1−1e≈0.63

Now, in the Huberman problem n is 5, which is not especially close to infinity, but luckily the convergence to the limit is pretty rapid.

Convergence of probability

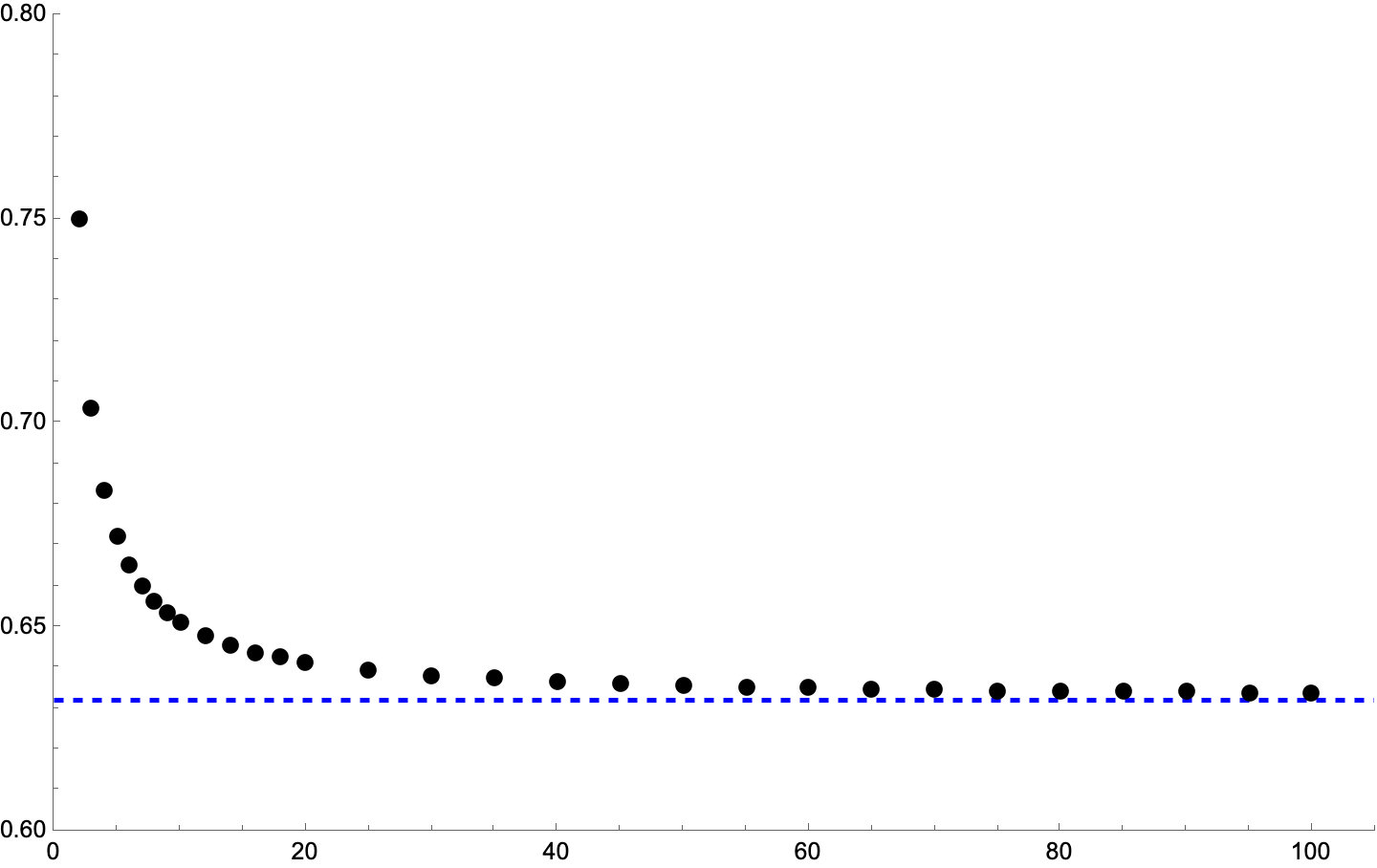
I would have guessed the answer for n=5 was about 0.65; it’s actually 0.67. Not super accurate, but better than 1.

Update 10 May 2024 12:21 PM
John D. Cook also saw the Huberman clip and wrote a nice post this morning about how adding probabilities is a reasonably close approximation if both

  • the base probability for a single trial is small; and
  • the number of trials is small.

Absolutely true, but not as much fun as a solution that ends up with Euler’s constant popping up out of nowhere.

  1. The clip is from this 4 hour, 22 minute (!) video episode of the Huberman Lab Podcast. Imagine if Huberman were John Gruber’s guest on The Talk Show. ↩

Next post Previous post