And now it’s all this

I just said what I said and it was wrong
Or was taken wrong

Next post Previous post

Gravity and Edgar Rice Burroughs

May 12, 2024 at 10:36 PM by Dr. Drang

Yesterday, I was thinking about what textbook I would move on to after I finish Adventures in Celestial Mechanics. Because I’ve been thinking about gravity, I pulled Oliver Kellogg’s Foundations of Potential Theory off my shelf and started leafing through it. I soon came upon a gravity problem that I first heard about when I was a teenager but never saw the solution for. The problem has to do with Pellucidar, and it’s not as tricky as I expected.

Pellucidar is an imaginary land created by Edgar Rice Burroughs for a series of pulpy adventure books, starting with At the Earth’s Core. The conceit of the stories is that the Earth is actually a hollow shell and that there’s an inhabited land, Pellucidar, on the inside surface of the shell. Intrepid adventurers from our side of the shell dig through to Pellucidar, meet the strange people and creatures who live there, and have adventures intrepidly. Never one to let an idea go unexploited, Burroughs even had Tarzan visit Pellucidar.

While I read one or two Tarzan books and several of the John Carter of Mars books, I never picked up any of the Pellucidar novels. But I did read somewhere—possibly in an Isaac Asimov science essay—that the concept of Pellucidar was flawed in a way apart from the many obvious ways: the inhabitants of Pellucidar would not “stick” to the inner surface of a hollow Earth because there’s no net gravitational force inside a spherical shell.

This seemed very odd to the teen-aged me, but Asimov (or whomever) didn’t explain it, and I didn’t have the analytical tools to check it out myself. But now I do, following more or less the derivation given by Kellogg.

Suppose we have a thin spherical shell of radius $a$. We want to know the gravitational attraction that the sphere exerts on a particle, $P$, which may be either inside or outside the sphere.

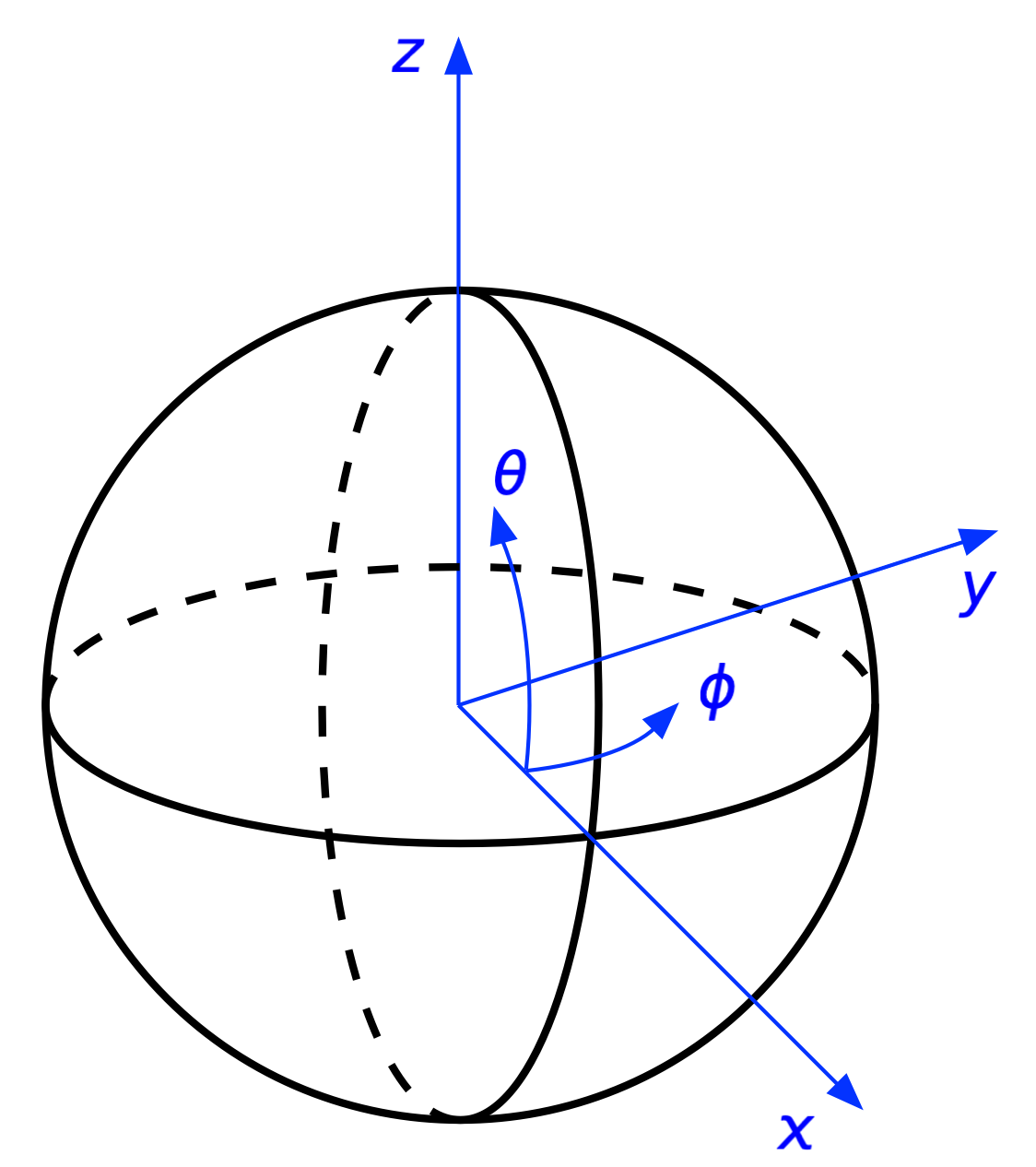
We’ll set up our coordinate system so that $P$ is on the $z$ axis. Every point on the sphere, $Q$, can be identified by two angular coordinates, $\theta$ and $\varphi$, which are the point’s latitude and longitude.

(If you’re wondering how we should handle the analysis if $P$ isn’t on the $z$ axis, don’t. One of the most important things to learn in mechanics is that the coordinate systems we use are up to us; there is no $x\text{-}y\text{-}z$ stamped on the universe. Wherever $P$ happens to be, we can draw a $z$ axis that runs through it from the center of the sphere.)

The gravitational force that some small differential element at $Q$ on the sphere exerts on particle $P$ is

$$dF=\frac{G\rho dA}{r^2}$$

where $G$ is the universal gravitational constant, $\rho$ is the areal density of the sphere (i.e., it has units of mass per area, not mass per volume), and $r$ is the distance from $Q$ to $P$. $dA$ is the differential area of the element on the sphere, and $dF$ is the differential force (per unit mass of $P$) that element exerts on particle $P$.

Here’s a sketch of the differential area at $Q$:

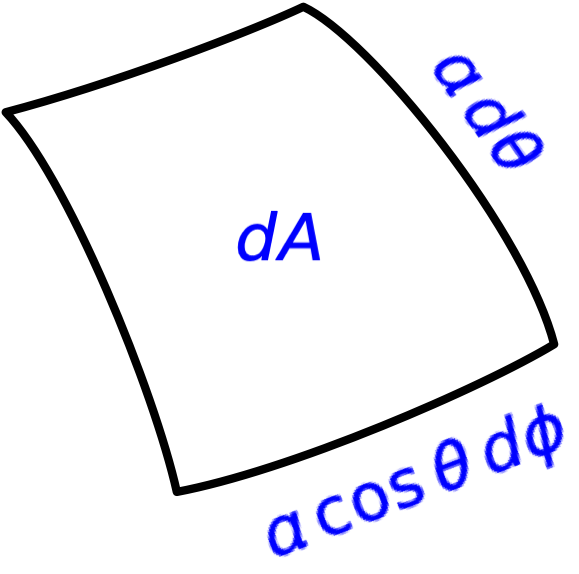
It’s bounded by lines of latitude that are $d\theta$ apart from one another and lines of longitude that are $d\varphi$ apart from one another. The area of the element is

$$dA=(ad\theta )(a\cos \theta d\varphi )=a^2\cos \theta d\varphi d\theta$$

If you’re wondering why we can use the formula for the area of a rectangle when the edges and the surface itself are curved, I will remind you that this is how calculus works. These differential lengths are teeny tiny and therefore the difference between the area of the surface and the area of a rectangle is extra extra teeny tiny. In calculus, we keep track of the teeny tiny and throw away the extra extra teeny tiny.

To express the differential force in terms of $\theta$ and $\varphi$, let’s look at a side view of the sphere with $P$ and $Q$. First, we’ll consider the case where $P$ is “above” $Q$:

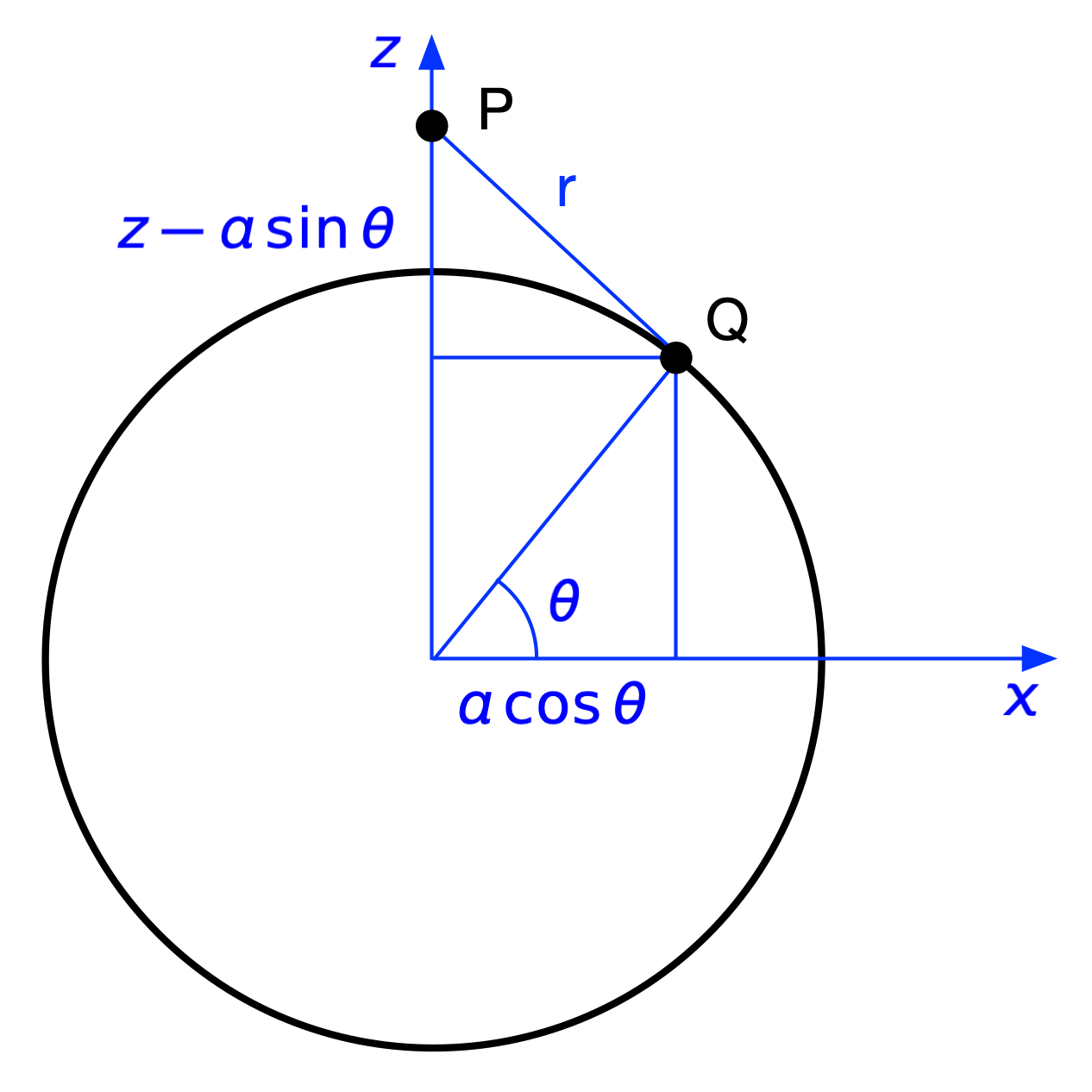
The distance between $P$ and $Q$ is

$$r=\sqrt{(a\cos \theta {)}^2+(z-a\sin \theta {)}^2}=\sqrt{a^2+z^2-2az\sin \theta }$$

Although I’ve drawn the figure with $P$ outside the sphere, the formula above also applies when $P$ is inside the sphere. What matters is that $P$ is above $Q$.

Now let’s consider the case where $P$ is “below” $Q$:

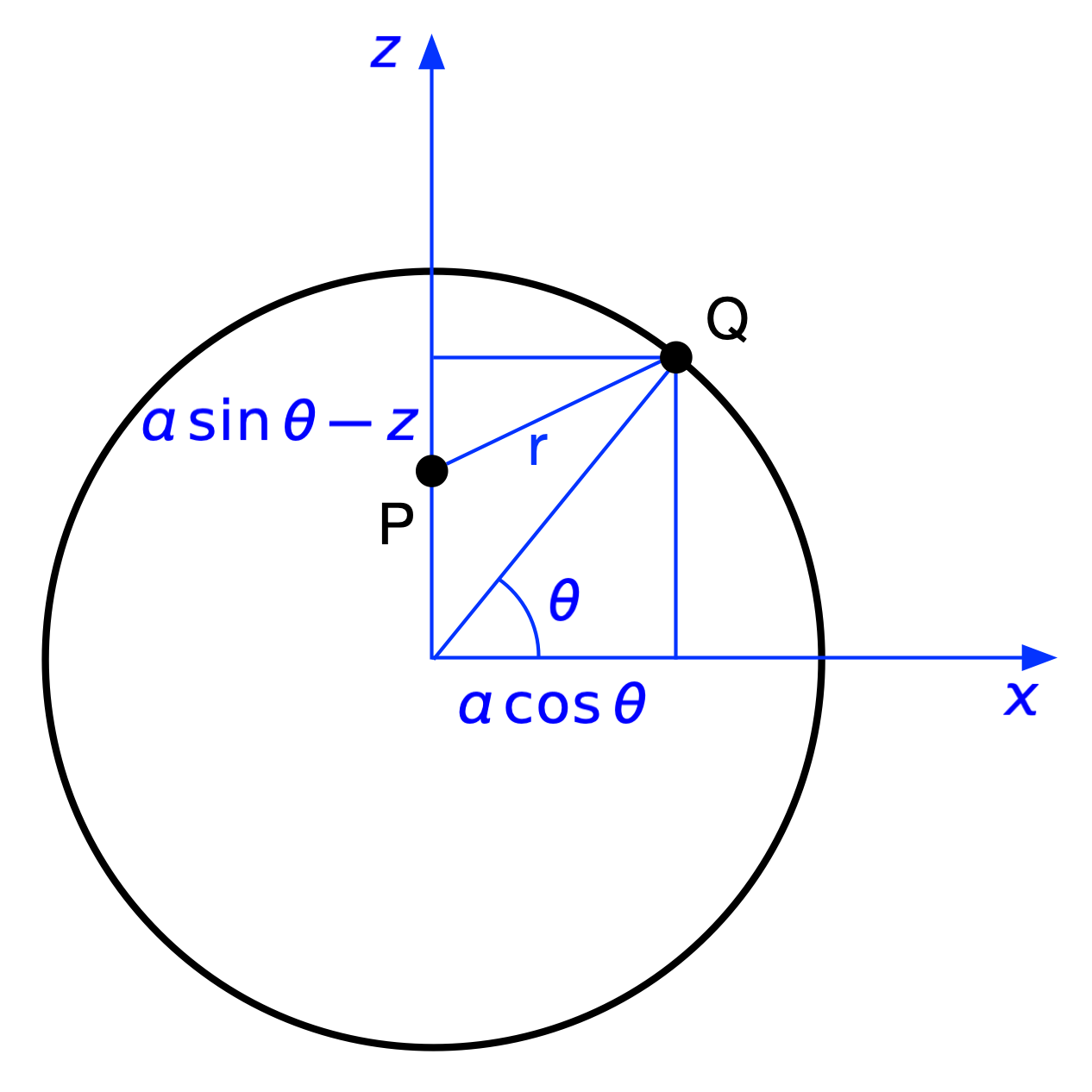
Here, $r$ is the hypotenuse of a different right triangle, but it turns out that

$$r=\sqrt{(a\cos \theta {)}^2+(a\sin \theta -z{)}^2}=\sqrt{a^2+z^2-2az\sin \theta }$$

is the same formula as before. That’s convenient. So the magnitude of the differential force is

$$dF=\frac{G\rho a^2\cos \theta }{\sqrt{a^2+z^2-2az\sin \theta }}d\varphi d\theta$$

To determine the force on $P$ due to the entire sphere, we’re going to integrate on $\theta$ from $-\pi /2$ to $\pi /2$ and on $\varphi$ from $0$ to $2\pi$. But first, we need to think about the direction of the differential force.

Note that in each of the two side views, the gravitational force on $P$ has two components: a component parallel to the $z$ axis (vertical in our drawings) and a component perpendicular to the $z$ axis (horizontal in our drawings). When we integrate over $\varphi$, we’re dealing with forces associated with a circle of constant latitude, and the components perpendicular to the the $z$ axis (horizontal) will cancel each other out. For example, the horizontal component when $Q$ is at $\varphi =180\text{°}$ cancels the horizontal component when $Q$ is at $\varphi =0\text{°}$, the horizontal component for $\varphi =270\text{°}$ cancels the horizontal component for $\varphi =90\text{°}$, and so on.

The upshot is that we only have to worry about the “vertical” component of the force, i.e., the component in the $z$ direction. To get that component, we multiply $dF$ by the $z$ direction cosine.

When $P$ is above $Q$, the $z$ direction cosine is

$$-\frac{z-a\sin \theta }{\sqrt{a^2+z^2-2az\sin \theta }}$$

where the minus sign out in front indicates that the component is acting in the negative $z$ direction. Remember, we’re computing the gravitational force on $P$ due to $Q$, so the force acts from $P$ toward $Q$.

When $P$ is below $Q$, the $z$ direction cosine is

$$\frac{a\sin \theta -z}{\sqrt{a^2+z^2-2az\sin \theta }}$$

Compare this formula with the previous one and you’ll see that they are algebraically identical. As with the expressions for $r$, the signs work out to give the same equation for both cases.

So the $z$ component of the differential force acting on $P$ due to $Q$ is

$$d{F}_z=\frac{G\rho a^2\cos \theta (a\sin \theta -z)}{(a^2+z^2-2az\sin \theta {)}^{3/2}}d\varphi d\theta$$

and the total force that the sphere exerts on $P$ is

$$F=F_z={\int }_{-\pi /2}^{\pi /2}{\int }_0^{2\pi }\frac{G\rho a^2\cos \theta (a\sin \theta -z)}{(a^2+z^2-2az\sin \theta {)}^{3/2}}d\varphi d\theta$$

This may seem awful, but it isn’t. First, notice that $\varphi$ doesn’t appear in the integrand, so the integral over $\varphi$ is just

$${\int }_0^{2\pi }d\varphi =2\pi$$

We can pull that and the other constants out to get

$$F=2\pi G\rho a^2{\int }_{-\pi /2}^{\pi /2}\frac{\cos \theta (a\sin \theta -z)}{(a^2+z^2-2az\sin \theta {)}^{3/2}}d\theta$$

This still looks bad, but with tools like Mathematica and SymPy, integrations like this aren’t the pain in the ass they used to be. After a few seconds of chugging in Mathematica,

the answer pops out:

$$F=\frac{2\pi G\rho a^2}{z^2}(sgn(a-z)-1)$$

where the signum function ($sgn$) is $+1$ if the argument is positive and $-1$ if the argument is negative. Therefore, if $P$ is outside the sphere ($a<z$),

$$F=\frac{2\pi G\rho a^2}{z^2}(-1-1)=-\frac{4\pi G\rho a^2}{z^2}$$

At this point, we recall that $4\pi a^2$ is the area of the sphere, so that multiplied by the areal density, $\rho$ , is the mass of the sphere, which we’ll call $M$. So for this case

$$F=-\frac{GM}{z^2}$$

which is just what we’d expect (remember that this is the force per unit mass of $P$, so there’s no mass term for the particle).

On the other hand, if $P$ is inside the sphere ($a>z$),

$$F=\frac{2\pi G\rho a^2}{z^2}(1-1)=0$$

which is the surprising (to me, anyway) result that the sphere exerts no net gravitational force on a particle inside it.

How can this be? Well, certainly it makes sense if $P$ is at the center of the sphere. If we move $P$ up from the center, there’s more mass below $P$ but it is, on the average, farther away. It works out that the increasing mass and increasing distance balance each other to keep the net force at zero.

Oliver Kellogg didn’t have Mathematica. His suggestion was to do a change of variable from $\theta$ to $r$ and then integrate. He doesn’t give any details of the process, just the two answers. But I went ahead and did it his way, too, using

$$r=\sqrt{a^2+z^2-2az\sin \theta }$$ $$dr=-\frac{az\cos \theta }{\sqrt{a^2+z^2-2az\sin \theta }}d\theta =-\frac{az\cos \theta }{r}d\theta$$

and

$$a\sin \theta -z=\frac{a^2-z^2-r^2}{2z}$$

With those substitutions, the integrand becomes

$$-\frac{1}{2a{z}^2}\frac{a^2-z^2-r^2}{r^2}$$

which is much easier to deal with than the original integrand. But we have to be careful with the limits. If $z>a$, the upper limit ($\theta =\pi /2$) becomes

$$r=z-a$$

and the lower limit ($\theta =-\pi /2$) becomes

$$r=z+a$$

Therefore, the integral is

$$F=\frac{\pi G\rho a}{z^2}{\int }_{z-a}^{z+a}\frac{a^2-z^2-r^2}{r^2}dr$$

where I got rid of the negative sign at the front of the integrand by exchanging the limits. With no trig functions to make life difficult, this works out very quickly to

$$F=-\frac{4\pi G\rho a^2}{z^2}$$

when $P$ is outside the sphere. This is the same answer as before.

If $z<a$, the upper limit ($\theta =\pi /2$) becomes

$$r=a-z$$

and the lower limit ($\theta =-\pi /2$) becomes

$$r=a+z$$

Therefore, the integral is

$$F=\frac{\pi G\rho a}{z^2}{\int }_{a-z}^{a+z}\frac{a^2-z^2-r^2}{r^2}dr$$

which works out to

$$F=0$$

when $P$ is inside the sphere. Again, a repeat of the answer we got when integrating over $\theta$.

While it was nice to see explicitly how Kellogg did the integration, it was faster to just let Mathematica do its thing. And I didn’t get any deeper physical insight doing the change of variable.

Anyway, now I understand the surprising thing I read about 45 or so years ago. And I’m downloading At the Earth’s Core.

Next post Previous post

Site search

Meta

• drdrang at leancrew
• Blog archive
• RSS feed
• JSON feed
• Mastodon
• GitHub repositories

Recent posts

Credits

This work is licensed under a Creative Commons Attribution-Share Alike 3.0 Unported License.

© 2005–2023, Dr. Drang