Next post Previous post

A factoring trick

May 17, 2024 at 6:23 PM by Dr. Drang

In Matt Parker’s latest video, he gives two proofs to show that if you

you’ll get a number that is a multiple of your original number minus one. In words, this seems magical; in equation form,

b n−1=(b−1)(something)

not so much. Certainly you know that

b 2−1=(b−1)(b+1)

because that comes up so often. You may also remember from algebra class that

b 3−1=(b−1)(b 2+b+1)

So it isn’t tremendously surprising to hear that b−1 is a factor no matter what n is. But what’s the proof?

Matt’s first proof is to notice that b=1 is a solution to

b n−1=0

for any n. Therefore, (b−1) has to be one of the factors of b n−1. He considers this a rather prosaic proof, and quickly moves on to the fun one, which involves expressing the numbers in different bases. It is a cute proof, and you should watch the video to see it.

But I wanted to go back to

b n−1=(b−1)(something)

and see if there’s a solution for something that works for every n. Obviously there is, or I wouldn’t have written this post. And you’ve probably already guessed what that solution is, but let’s figure it out systematically.

We’ll set up the polynomial division of b n−1 by b−1 and run it out for a few steps:

Polynomial division

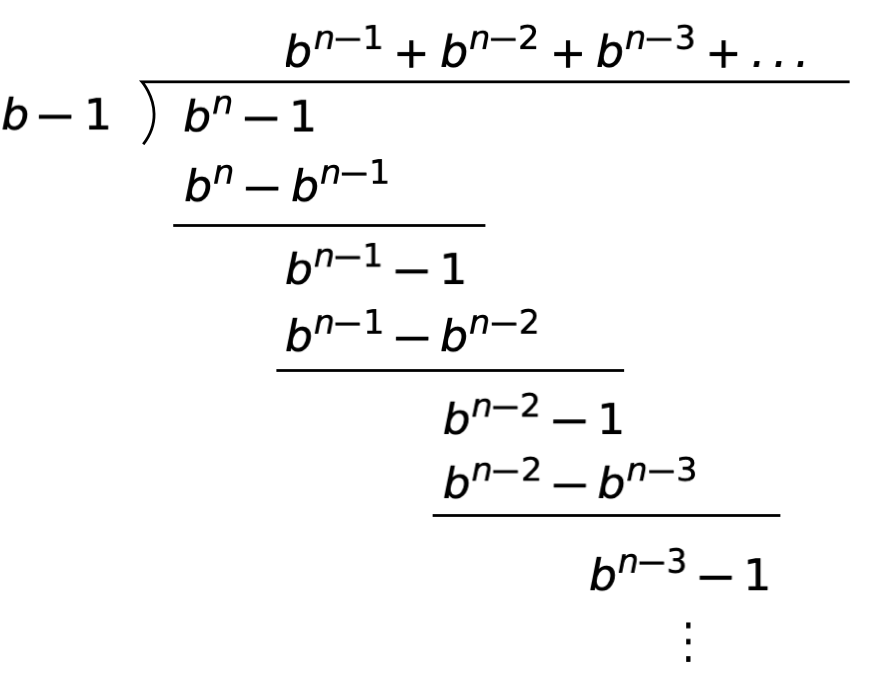
As you can see, after Step m in the process, the difference (i.e., the expression under the horizontal line) is

b n−m−1

So after m=n−1 steps, the difference will be b−1, which means that the last term in the quotient will be +1 and there will be no remainder. Therefore, something is

b n−1+b n−2+…+b+1=∑ m=0 n−1b m

which is easier to remember than I would have guessed.

Next post Previous post