Simple phone bending
March 18, 2025 at 8:47 PM by Dr. Drang
Here’s a simple problem assigned to me by John Siracusa. He was the guest host on this week’s episode of Upgrade, and early in the show he and Jason Snell were discussing the “thin iPhone” that’s rumored to be coming out this fall. Apparently, there will be only one size of this phone, and there’s speculation that there won’t be a “Plus” or “Max” size because of concerns about another Bendgate. John thought that an unlikely reason, which led to my homework:
We need some materials engineer like Dr. Drang to do the math in this, but… how much additional bending power do you have for the mere millimeters of extra length and width that you would get with whatever the max size is?
I’ll start by pointing out that I’m not a materials engineer, I’m a structural engineer, which is good because that’s the kind of engineer you want to do this type of calculation. I have nothing against materials engineers, but you wouldn’t want to call an oncologist to treat a heart condition, would you?
Anyway, the bending John is concerned with is elementary uniaxial bending of the iPhone chassis, specifically the bending of the siderails that run in the long direction of the phone. To determine the effect of force and length on bending the siderails, we model them as a simply-supported beam with a concentrated load at the center. The bending of such a beam is controlled by the bending moment. Structural engineers are taught to construct moment diagrams to determine the maximum bending moment.
Here’s an edge-on sketch of the phone with the load and support conditions of interest. Below that is the corresponding moment diagram.
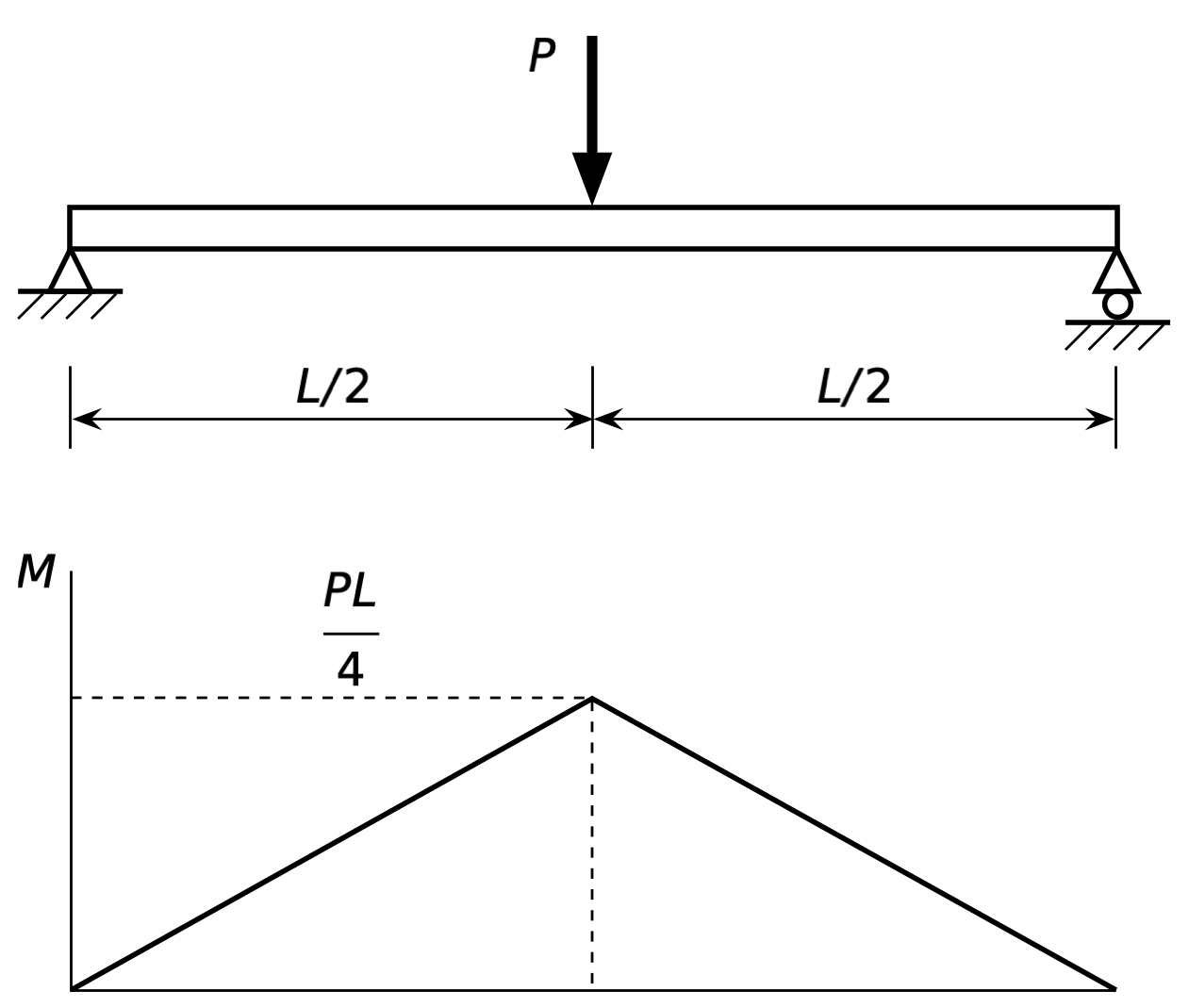
This is one of the first problems we learn how to solve. The peak moment is at the center of the beam and is
This comes from multiplying the reaction at either support, , by its distance from the center, .
So the peak bending moment, which is what determines whether the beam will undergo permanent deformation, is a linear function of both the load and the length. So if the beam is lengthened by 10%, which is about how much longer an iPhone Pro Max is compared to an iPhone Pro, the moment will increase by 10%. And if we make the reasonable assumption that the siderails of a Max-sized phone will have the same cross-section as siderails of a non-Max phone, then the bending stress will also increase by 10%. Not a lot.
Could there be structural concerns other than a repeat of Bendgate? Sure. But since I don’t know the internal structure of this speculative thinner iPhone, I have no way to analyze it. Without any more information, I’d have to say John is right and the length of the thinner iPhone is not being restricted for structural reasons.
Update 19 Mar 2025 7:06 AM
OK, after sleeping on it, I’ve decided to add a little nuance here. While a 10% increase in stress isn’t much, it could reduce the phone’s factor of safety against bending failure to a value lower than Apple allows. I tend to think, though, that if Apple really wanted to make a thin phone that was longer and wider, they’d tweak the design of the siderails to increase their strength and bring the factor of safety back up to their standard.
