ChatGPT and beam bending redux

July 24, 2025 at 9:07 PM by Dr. Drang

A couple of years ago, I asked ChatGPT to solve two simple structural analysis problems. It failed pretty badly, especially on the second problem, where it wouldn’t fix its answer even after I told it what it was doing wrong. Earlier this week, I decided to give it another chance.

Here’s my statement of the problem:

A cantilever beam of length L has a concentrated load P applied at its midpoint. The modulus of elasticity is E and moment of inertia is I. What is the formula for the tip deflection?

There was, as usual, a lot of blather in ChatGPT’s response, but paring it down, its answer was

δ_{t i p} = \frac{5 P L^{3}}{48 E I}

which is correct. If you want to see why this is the answer, you can go look at my two-year-old post and—oh, who am I kidding? Here’s the problem:

Cantilever beam with load at center

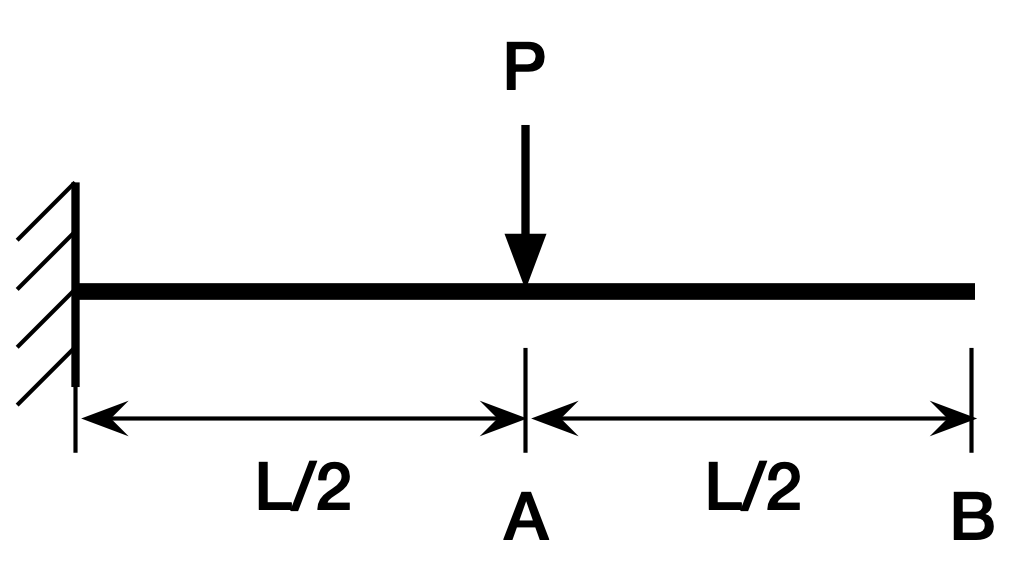
The key to determining the deflection at B is to recognize that the left half of the beam is a cantilever beam in its own right, with a length of $L / 2$ and a load $P$ at its tip. And the right half of the beam doesn’t bend at all, it’s just carried downward and tilted by its connection to the left half of the beam.

Cantilever beam deflection pattern

The deflection and rotation at the end of the left half of the beam (Point A) have well known solutions:

δ_{A} = \frac{P {(\frac{L}{2})}^{3}}{3 E I} = \frac{P L^{3}}{24 E I}

and

θ_{A} = \frac{P {(\frac{L}{2})}^{2}}{2 E I} = \frac{P L^{2}}{8 E I}

δ_{B} = δ_{A} + θ_{A} (\frac{L}{2}) = \frac{P L^{3}}{24 E I} + \frac{P L^{2}}{8 E I} (\frac{L}{2}) = \frac{5 P L^{3}}{48 E I}

which is just what ChatGPT said.

Unfortunately, ChatGPT got cocky and finished its response with this:

If you’d like a derivation step-by-step or a diagram to visualize the moment curves and deflection, I can provide that as well.

I told it to explain how it got its answer, and that’s when things went south.

First, it divided the beam into two regions, just as I did. It called the left half Region I, the right half Region II and it set the origin of its x-axis at the fixed end. It then said the bending moments were

M_{I} (x) = - \frac{P L}{2}

in the left half and

M_{I I} = - P (L - x)

in the right half. Since both of these are wrong, I wondered how it got the right answer, so I continued reading.

In both halves, it integrated the nearly¹ correct differential equation,

E I \frac{d^{2} y}{d x^{2}} = M (x)

to solve for the deflection function, $y (x)$ .

The integration has to be performed twice in each half of the beam, so you end up with four constants of integration. Remarkably, ChatGPT showed the values for only two of the constants, and said the others could be determined through “standard algebra.”

ChatGPT's initial incomplete solution

Of course, if you apply standard algebra and solve for $C_{3}$ and $C_{4}$ , you’ll get values that don’t lead to the correct tip deflection. You can’t, because you started with the wrong bending moments.

So I had ChatGPT go through the lengthy algebra to get the values of $C_{3}$ and $C_{4}$ and then plug them into its equation for the tip deflection. It took a while, but eventually ChatGPT had an epiphany:

ChatGPT realizes there is an error

Yes, something’s definitely wrong. It went off on a long quest to find an algebra error in its work. But there was no algebra mistake, so it decided that its initial correct answer of

δ_{t i p} = \frac{5 P L^{3}}{48 E I}

was wrong, and the correct answer was

δ_{t i p} = \frac{11 P L^{3}}{48 E I}

My response:

No, your original answer is correct. Your equations for the moments in both regions are wrong. What I don’t understand is how you got the right answer in the first place. I suspect you found it somewhere, and didn’t actually go through any of the (incorrect) analysis you showed me when I asked for your reasoning.

In other words, all the “reasoning” it had been showing me was not merely wrong, it was bullshit. That was not how it got the original answer. During its lengthy reply, ChatGPT said it pulled its original correct answer from a “standard solution.” Standard seems to be its favorite word for indicating that it’s doing things right and we shouldn’t question it.

I asked where it got the correct answer, and it said it came from “standard [sic] references in structural mechanics,” including

Roark’s Formulas for Stress and Strain.
AISC Steel Construction Manual.
AISC Design Guide 3.
Mechanics of Materials by Gere and Timoshenko.
Mechanics of Materials by Beer, Johnston, DeWolf, and Mazurek.

I have all five of these books, and none of them have the answer ChatGPT gave. But three of them—Roark, the AISC manual, and Gere & Timoshenko—include general formulas for a cantilever beam with a concentrated load somewhere along its length. A reasonable person could use the formulas in those books to get the correct answer by plugging in $L / 2$ as the location of the load.

Once again, though, ChatGPT puts its foot in its mouth by making something up. Before I could ask for more specific references within these books, it gave me this:

ChatGPT gives an incorrect reference

My reply:

I have the 6th edition of Roark, and Table 8 doesn’t cover this problem. Did you make up that reference?

Well. After some hemming and hawing, it said that its answer came from this general formula in Roark,

δ = \frac{P a^{2}}{6 E I} (3 L - a)

where it plugged in $a = L / 2$ and simplified.

Which would be a good answer if Roark had that formula in it, but it doesn’t. In the formula ChatGPT just gave, a is the distance of the load from the fixed end of the beam. Roark gives a different formula because it takes a to be the distance of the load from the free end. So another bullshit answer.

Oh, and ChatGPT said this formula is in Table 27 of Roark. Table 27 has nothing to do with beam bending.

A glutton for punishment, I continued my Socratic dialog with a stochastic parrot:²

Again, Table 27 in Roark doesn’t cover beams of any kind. The formula you’re using is from Gere and Timoshenko’s book, which I also have. Tell me where it is in that book.

Once again, ChatGPT told me I was right and said the formula was in Chapter 5 of Gere & Timoshenko. You will be shocked to hear that Chapter 5 doesn’t cover deflections of beams. Chapter 7 does, but the formula isn’t there, either. It’s in Appendix G, a fact I was never able to extract from the conversation. In fact, ChatGPT ultimately decided the formula wasn’t in Gere & Timoshenko at all.

After scrolling through many more words of apology and justification, I asked this:

Throughout this conversation, I have been the source of your knowledge. How can you use the person asking the question as your source?

More apologies followed, along with an offer to do the derivation correctly. I took a deep breath, said go ahead, and… it did the problem correctly! Well, except for the sign error I mentioned in a footnote earlier in the post. Its “explanation” of the sign error was even more hand-wavy than any of its other bullshit explanations, and I abandoned the conversation. If you’re of a masochistic bent, you can see it all here.

So what did I get out of this exercise?

OpenAI seems to have done a lot more plagiarism in the past two years. I own my copies of the references ChatGPT cited. I bet OpenAI doesn’t.
The plausibility of the answers has improved, especially when it comes to mathematics. You may have noticed in the screenshots that ChatGPT is formatting equations nicely now, which makes it seem more authoritative. Two years ago, the formulas it presented looked like this:

δ = (P * L^3) / (3 * E * I)

Of course, plausible doesn’t mean correct.
ChatGPT still believes that long answers sound more reliable. In fact, it may be giving even longer answers than before. To me, this is frustrating, but maybe its regular users like it. Which doesn’t say much for them.
It still makes up references, the classic hallucination problem. And it doesn’t seem to care that I told it I had the books it was citing—it still happily give me bogus chapters, tables, and page numbers. Perhaps it didn’t believe me.
I suppose it’s possible that I’d get better answers from a better model if I were a paying customer. But why would I pay for something that can’t demonstrate its value to me?
The most disturbing thing is its inability to give a straight answer when asked how it arrived at a solution. Maybe if I were Simon Willison, I’d know better how to get at its actual solution process, but I don’t think I should have to have Willison-level expertise (which I could never achieve even if I wanted to) to get it to explain itself.

Maybe I shouldn’t put so much emphasis on ChatGPT’s inability to explain itself. After all, I didn’t ask it to explain how it came up with the SQL code I wanted a few months ago. But to me, the code it gave me was self-explanatory; I could read it and see what it did and why. And I could test it. Not so with the beam deflection problem. Being able to explain yourself and cite proper references is the way ensure this kind of answer is correct.

There’s a sign error if you define positive deflections and moments in the usual way, which ChatGPT does. ↩
Credit to Emily Bender, et al. ↩

And now it’s all this

I just said what I said and it was wrong
Or was taken wrong

ChatGPT and beam bending redux

Site search

Meta

Recent posts

Credits

And now it’s all this

I just said what I said and it was wrong Or was taken wrong

ChatGPT and beam bending redux

Site search

Meta

Recent posts

Credits

I just said what I said and it was wrong
Or was taken wrong