Next post Previous post

ChatGPT and beam bending

June 14, 2023 at 1:33 PM by Dr. Drang

There’s an internet law that everyone must blog about ChatGPT, and I’m way behind, so here we go. I think what I have to say is something new.

I was inspired by reading the concerns that many faculty members have about students using large language models like ChatGPT to write their term papers for them. I wondered whether LLMs would be be of any use in solving the kinds of engineering problems I typically assigned (or was assigned, if we go back to my student years). I signed up for an OpenAI account and tried out ChatGPT on a few simple structural analysis problems.

I can’t say I went into this with an open mind—I expected ChatGPT to do poorly. My expectation was based on a couple of things:

  1. I’d read Stephen Wolfram’s good—albeit overlong—explanation of how LLMs work. It matched up pretty well with my many years of experience with what I guess should be called small language models. This started back in 1983, when I read this Computer Recreations article by Brian Hayes in Scientific American. Hayes used letter frequencies from particular pieces of literature to generate nonsense text that had the “sound” of the original. Much later, I played with the Dissociated Press tool in Emacs, which uses a similar algorithm to scramble whatever text is in the current buffer. Finally, I wrote a “lipsum” script using the Games::Disassociate Perl module to generate random text from Darwin’s Origin of Species. I still call that script from Keyboard Maestro whenever I need a paragraph of placeholder text:

    The steeper shores would be destroyed, almost as much isolated will still resemble each other. Therefore it need not be standing room for his own good; but to change it should not forget that to range into new countries. In their new homes, each kind will have been but little modified, and they will not be a cheering prospect; but we shall surely be enabled to discuss what circumstances are favourable to its increase whether some one or in any part of the now.

    Is it ironic that the ideas used 40 years ago to generate drivel (Hayes’s word) are now being called artificial intelligence? You might very well think that. I couldn’t possibly comment.

  2. Because LLMs are text-based, and structural analysis problems are not especially text-based, I didn’t think ChatGPT would have much to go on. The corpus on which ChatGPT draws to get its answers just isn’t, I thought, filled with structural analysis examples. And whatever examples it sucked up during its learning phase are likely to be mostly sketches with very little surrounding text.

    This is in contrast to one of ChatGPT’s successes: writing short computer programs. The internet is loaded with source code and comments describing what the source code does. In this application, ChatGPT is sort of an automated front end to Stack Overflow.

But my expectation could be wrong. Here was my first question to ChatGPT:

What is the center deflection of a simply supported steel beam that’s 24 feet long, has a moment of inertia of 100 in^4, and is subjected to a uniform load of 2000 lb/ft?

And here was its answer:

To determine the center deflection of a simply supported steel beam, we can use the formula for deflection due to a uniform load. The formula is:

δ = (5 * w * L^4) / (384 * E * I)

Where:
δ is the deflection at the center of the beam
w is the uniform load applied to the beam (2000 lb/ft in this case)
L is the length of the beam (24 feet in this case)
E is the modulus of elasticity of the material (steel in this case)
I is the moment of inertia of the beam cross-section (100 in^4 in this case)

The modulus of elasticity of steel typically ranges from 29,000 ksi to 30,000 ksi. Let’s use a value of 29,000 ksi for this calculation.

Plugging in the given values into the formula, we get:

δ = (5 * 2000 * 24^4) / (384 * 29000 * 100)

Calculating this expression, we find:

δ ≈ 1.79 inches

Therefore, the center deflection of the simply supported steel beam under the given conditions is approximately 1.79 inches.

Some of this is quite good. The formula,

δ=5wL4384EI\delta = \frac{5wL^4}{384EI}

is the correct equation for the center deflection of a simply-supported beam with a uniform load. It’s also using the symbols that structural engineers (here in the US, anyway) use most often for load, length, modulus of elasticity, and moment of inertia. And 29,000 ksi is what structural engineers use for the modulus of elasticity of steel.1

Of course, the numerical answer is nonsense. First, because ChatGPT didn’t use consistent units. You can’t use feet in one part of the equation and inches in another, nor can you use kips in one part and pounds in another.2 More surprising to me, though, was its failure to run out the numerical calculation correctly.

5·2000·244384·29,000·100=2.98\frac{5\cdot2000\cdot24^4}{384\cdot 29,000 \cdot 100} = 2.98

not 1.79. If a computer can’t do a simple calculation correctly, how can you trust it to do anything?

And if you’re wondering whether ChatGPT really was converting the units behind the scenes without telling us, the correct answer using consistent units is

5(2/12k/in)(288in)4384(29,000k/in2)(100in4)=5.15in\frac{5 \; (2/12 \; \mathrm{k/in}) \; (288 \; \mathrm{in})^4}{384 \; (29,000 \; \mathrm{k/in^2})\; (100 \; \mathrm{in^4})} = 5.15\; \mathrm{in}

Later, I told ChatGPT that it couldn’t mix feet and inches, that it needed to use consistent units. From that point on, it converted feet to inches and ksi to psi before plugging the numbers into the equations. That was good, but it didn’t fix the arithmetic errors, which continued.

Strictly speaking, this wasn’t good example of a structural analysis homework problem. Students don’t get asked to just look up formulas and plug in numbers. More likely, they’d be asked to derive the equation that ChatGPT started with by either solving the differential equation for beam deflection or using some simplified technique like the moment-area or conjugate beam method. I didn’t think asking ChatGPT to do something like that would be fair.

For a problem that could be solved by looking up formulas and combining them in an intelligent way, I tried this problem, where I asked for the deflection and slope at the right end of the beam:

Cantilever beam with load at center

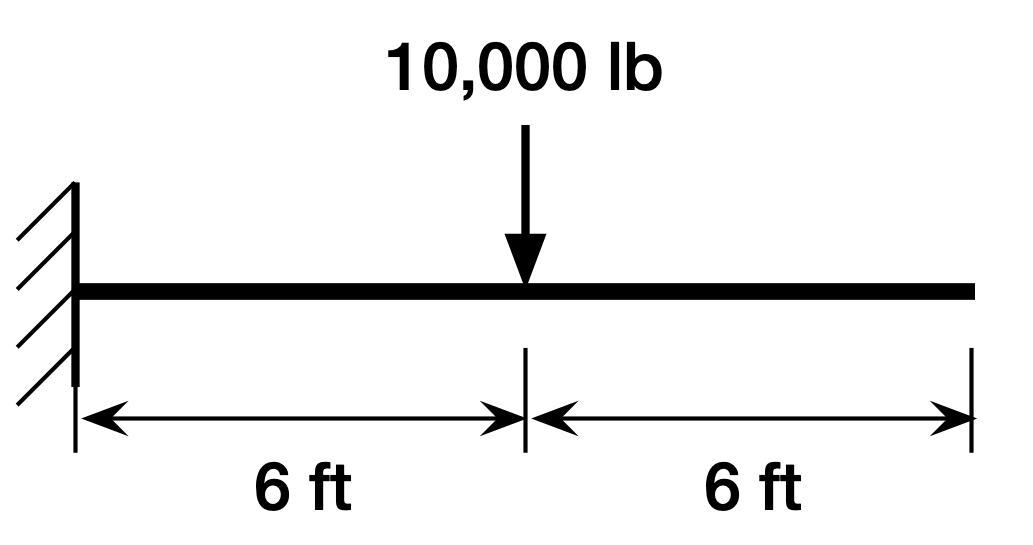
Here was my conversation with ChatGPT:

What are the deflection and slope at the free end of a cantilever beam? The beam is 12 feet long, has a moment of inertia of 100 in^4, and is made of steel. It is subjected to a concentrated load of 10,000 lbs at its center.

To determine the deflection and slope at the free end of a cantilever beam, we can use the formulas for beam deflection and slope.

The deflection (δ) at the free end of a cantilever beam under a concentrated load can be calculated using the formula:

δ = (P * L^3) / (3 * E * I)

where:
P = concentrated load (10,000 lbs in this case)
L = length of the beam (12 ft)
E = modulus of elasticity of the material (steel)
I = moment of inertia of the beam

The slope (θ) at the free end of a cantilever beam can be calculated using the formula:

θ = (P * L^2) / (2 * E * I)

Using the given values:

P = 10,000 lbs
L = 12 ft
E = 29,000,000 psi
I = 100 in^4

First, let’s convert the length from feet to inches: L = 12 ft * 12 in/ft = 144 in

Substituting the values into the formulas, we can calculate the deflection and slope:

δ = (10,000 lbs * (144 in)^3) / (3 * 29,000,000 psi * 100 in^4)

θ = (10,000 lbs * (144 in)^2) / (2 * 29,000,000 psi * 100 in^4)

Now we can calculate the deflection and slope.

Finish the calculations.

Apologies for the delay. Let’s continue with the calculations to determine the deflection and slope at the free end of the cantilever beam.

Given:
P = 10,000 lbs
L = 144 in
E = 29,000,000 psi
I = 100 in^4

Using the formulas for deflection and slope:

Deflection (δ):
δ = (P * L^3) / (3 * E * I)
= (10,000 lbs * (144 in)^3) / (3 * 29,000,000 psi * 100 in^4)
≈ 1.619 in

Slope (θ):
θ = (P * L^2) / (2 * E * I)
= (10,000 lbs * (144 in)^2) / (2 * 29,000,000 psi * 100 in^4)
≈ 0.262 rad or 15.01 degrees

Therefore, the deflection at the free end of the cantilever beam is approximately 1.619 inches, and the slope at the free end is approximately 0.262 radians or 15.01 degrees.

In this problem, ChatGPT has used consistent units, but that’s the only positive. As before, it does the arithmetic incorrectly. And while the formulas it uses for deflection and slope,

δ=PL33EI\delta = \frac{PL^3}{3EI} θ=PL22EI\theta = \frac{PL^2}{2EI}

are well known, they’re for a cantilever with a load at its tip,

Cantilever beam with load at tip

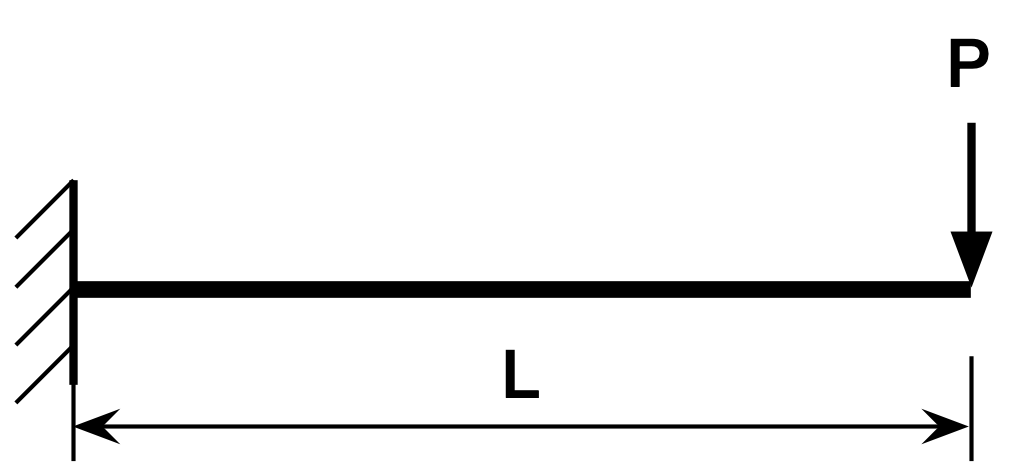
not the problem that was given. Clearly, ChatGPT focused on the phrases cantilever beam, concentrated load, and deflection and slope, and that’s how it pulled these equations out of its training material.

Interestingly, if I had assigned this problem, I would expect the students to use these same two equations to calculate the answers, but the equations would be part of the process of solution, not the solution as a whole.

Here’s how you do it. You recognize that the left half of the beam acts like a cantilever with a concentrated load at the tip and that the right half just “goes along for the ride,” remaining straight but at a slope. This is because there’s no bending moment in the right half of the beam. Continuity at the center of the beam means that the deflection and slope at that point are continuous from left half of the beam to the right half. In pictures, we’d see it like this:

Curved and straight portions of cantilever beam

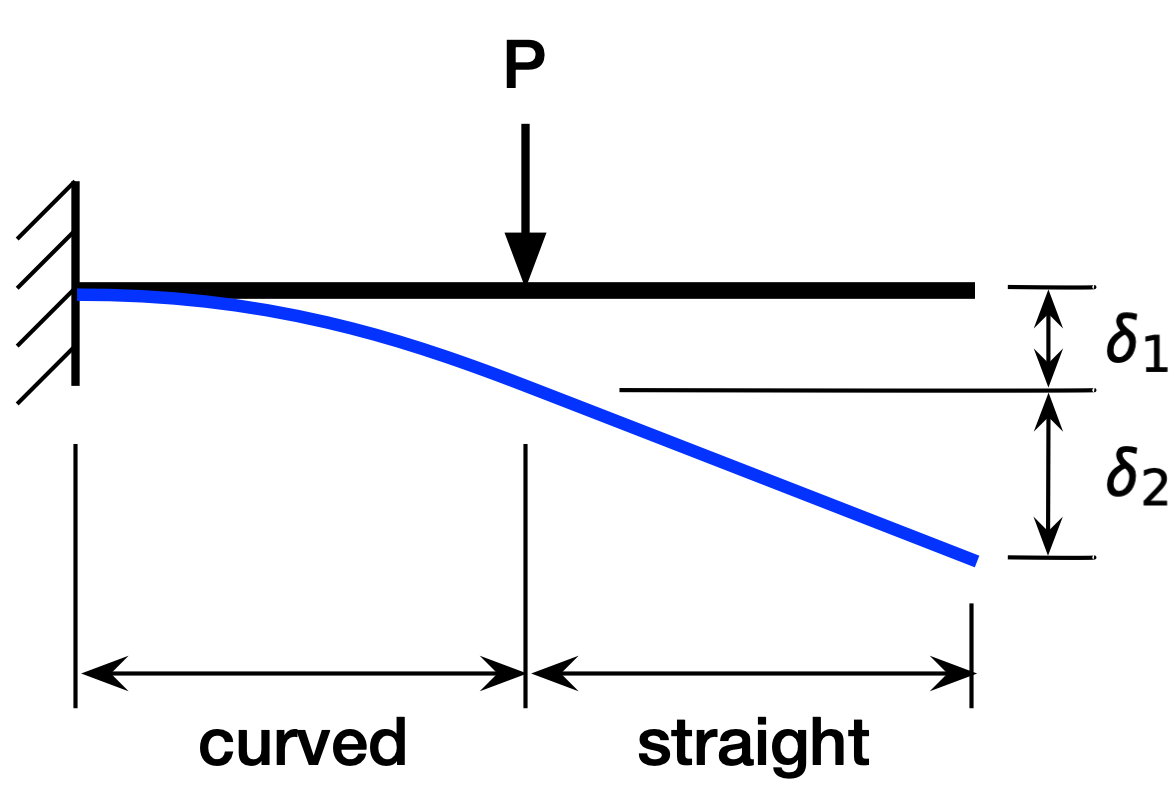
So the slope at the free end of the beam is the same as the slope at the center,

θ=P(L2)22EI=PL28EI\theta = \frac{P\left(\frac{L}{2}\right)^2}{2 EI} = \frac{P L^2}{8EI}

and the deflection at the free end is the sum of the deflection at the center and the vertical drop of the straight half, which is the product of its slope and length,

δ=δ1+δ2=P(L2)33EI+PL28EIL2=5PL348EI\delta = \delta_1 + \delta_2 = \frac{P \left(\frac{L}{2}\right)^3}{3EI} + \frac{P L^2}{8EI} \frac{L}{2} = \frac{5 PL^3}{48 EI}

(There are no sines or tangents in the equation because the angles are small and the sines and tangents are taken to be equal to the angles themselves. That’s one of the fundamental assumptions of linearly elastic structural mechanics.)

You aren’t likely to find these equations in a table of beam solutions, because there are only so many problems you can fit in a table. The idea behind most tables of solutions is that while sometimes they can be used directly—as with the simply-supported beam with a uniform load—often they have to be used in combination with other structural engineering concepts.

I tried to get ChatGPT to recognize that it was using formulas that were appropriate for a load at the end of the beam, not at the center. It apologized (as it always does) and reiterated the solution using the same incorrect formulas. Despite reusing the same formulas and the same input values, it got different numerical answers because it can’t do arithmetic.

I’m glad I did this exercise. It’s one thing to say “LLMs aren’t intelligent” because you have some vague sense of how they work; it’s another to see how they try to answer questions on a topic you know very well. Your expertise allows you to see where they got their knowledge and how they misused it.

  1. Mechanical engineers tend to use 30,000 ksi. I’ve never understood why we have this cultural difference. ↩

  2. A kip is a “kilopound,” or 1000 pounds. So “ksi” stands for “kips per square inch.” Put another way, 1 ksi = 1000 psi. ↩

Next post Previous post