Next post Previous post

Parabolic mirrors made simple(r)

May 29, 2023 at 12:09 PM by Dr. Drang

A couple of days ago, Numberphile released a video on YouTube in which Tom Crawford explained why parabolic mirrors reflect incoming light to the focal point. His explanation was, I thought, needlessly complicated, so I decided to write up a simpler one. No implicit differentiation, no vector algebra, no messing around with square roots of polynomials.

Here’s Tom’s explanation:

First, I don’t think Tom does his audience any favors by starting with a parabola that opens to the right. Most people are used to parabolas that open upward and have this simple equation

y=bx2y = bx^2

where b controls the spread of the parabola. Using this equation is especially helpful when you want to get the slope,

dydx=2bx\frac{dy}{dx} = 2bx

because this is one of the first derivatives you learn in calculus.

Sometimes, doing the unexpected can lead to nice simplifications, but that doesn’t happen in Tom’s analysis, so let’s make our parabola follow the equation above.

Parabola construction with tangent, focal point, and light rays

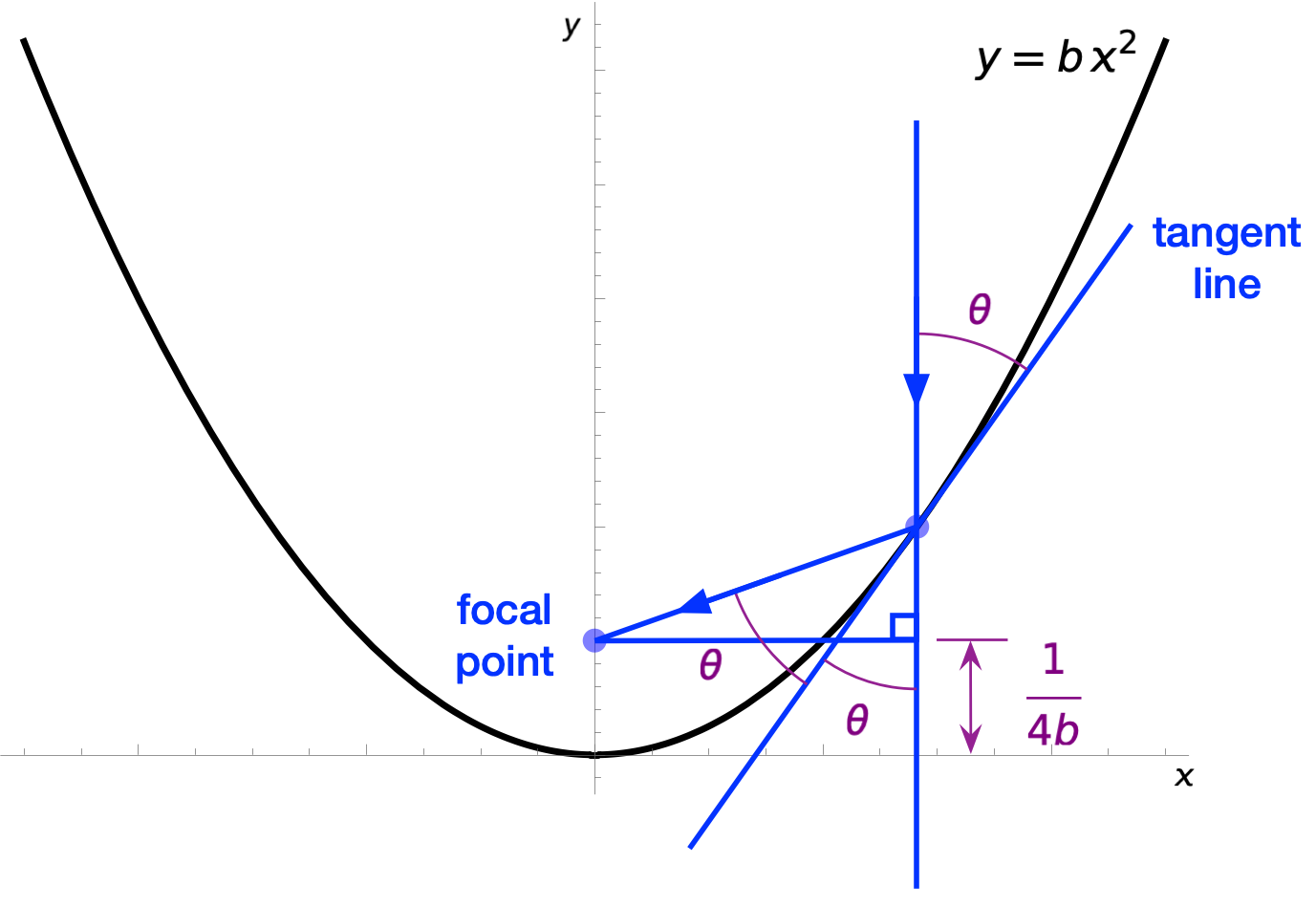
As you can see, I’ve added the focal point (or focus), which is on the y-axis at a distance 1/4b1/4b above the vertex. If it’s been a while since you took analytic geometry, you may have forgotten where the focus is, but that’s the spot. (If you’re wondering about the directrix, it’s parallel to the x-axis and 1/4b1/4b below it, but we won’t need that in our analysis.)

The figure also includes a line tangent to the parabola at some general point, (x,bx2)(x, bx^2) and some signal (a light or sound wave) that comes in parallel to the y-axis, bounces off the parabola and goes through the focal point. Physics says the incident and reflected beams are at the same angle, θ\theta, to the tangent line. We get the other θ\theta, the one on the lower right, from geometry: it’s on the opposite side of intersecting lines from the upper θ\theta.

Our job is to prove that the above construction is true, that the reflected beam passes through the focal point for any point on the parabola. To do that, let’s redraw the triangles from the above diagram a little bigger and identify some other dimensions and angles.

Triangles from parabola construction

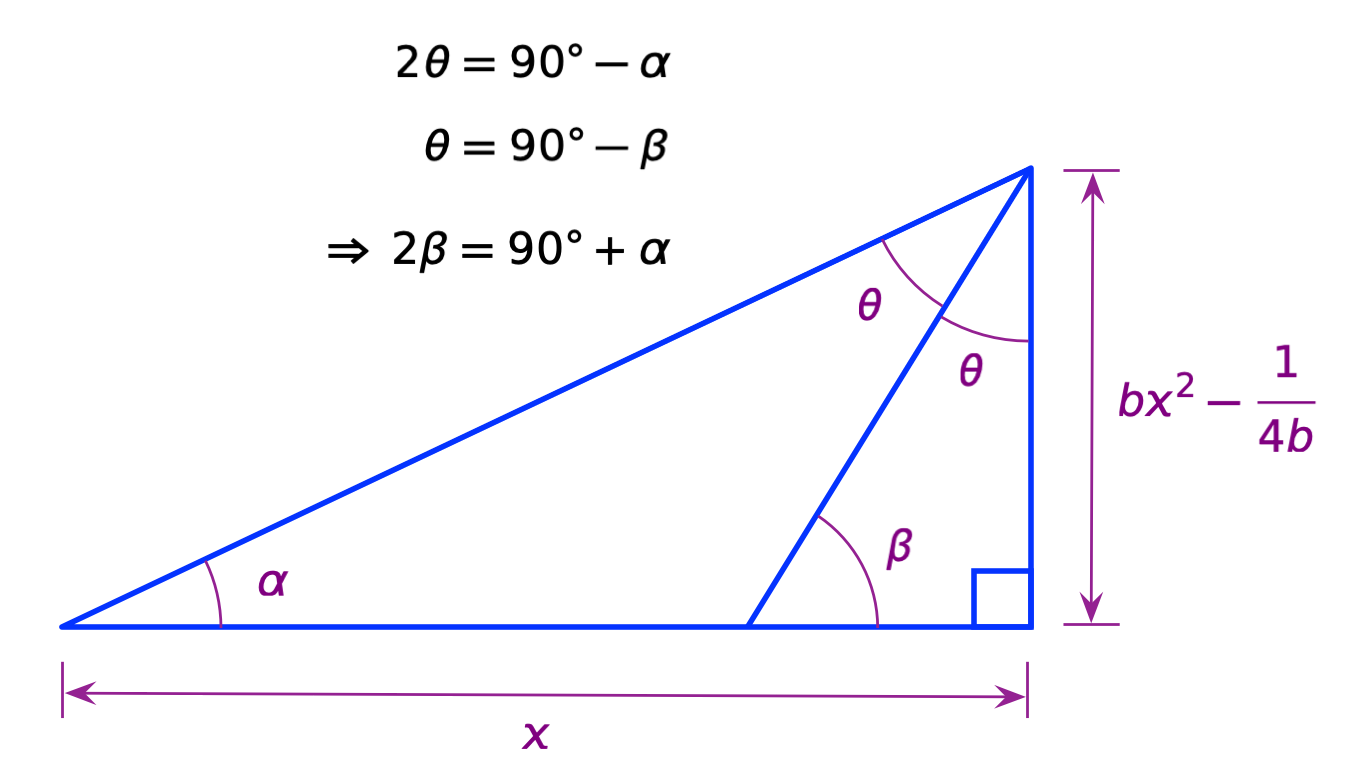
Here, α\alpha is the angle of the line from the reflection point to the focus and β\beta is the angle of the tangent line through the reflection point. As you can see from the larger triangle,

2θ=90∘−α2 \theta = 90^\circ - \alpha

and from the smaller triangle,

θ=90∘−β\theta = 90^\circ - \beta

Combining these equations gives us this relationship between α\alpha and β\beta:

2β=90∘+α2\beta = 90^\circ + \alpha

If we prove that this is true, we’ve shown that the reflected beam goes through the focus.

We know that the tangent of β\beta is the derivative of the parabola, 2bx2bx, and we can work out the tangent of α\alpha from the dimensions given in the figure. So let’s take the tangent of both sides of the above equation and see what happens.

For the left side, we use this double angle formula for tangent:

tan(2β)=2tanβ1−tan2β=2(2bx)1−(2bx)2=4bx1−4b2x2\tan (2\beta) = \frac{2 \tan \beta}{1 - \tan^2 \beta} = \frac{2 (2bx)}{1 - (2bx)^2} = \frac{4 b x}{1 - 4 b^2 x^2}

For the right side, we use this trig identity,

tan(90∘+α)=−cotα\tan (90^\circ + \alpha) = - \cot \alpha

and the lengths given for the sides of the larger triangle to get

−cotα=−xbx2−14b=−4bx4b2x2−1=4bx1−4b2x2-\cot \alpha = -\frac{x}{b x^2 - \frac{1}{4b}} = -\frac{4bx}{4b^2x^2 - 1} = \frac{4 b x}{1 - 4 b^2 x^2}

This proves that

tan(2β)=tan(90∘+α)\tan (2\beta) = \tan (90^\circ + \alpha )

and therefore

2β=90∘+α2\beta = 90^\circ + \alpha

and that’s what we set out to prove. Because this is true for any value of x, any vertical beam hitting the parabola will be reflected to the focal point.

When Tom turned his lines into vectors and started taking dot products, I thought he was doing something clever to make his later algebra easier. But as you saw from his messing around with square roots of polynomials, it didn’t make the algebra easier, it made it harder.

Should I point out that Tom’s flashlight probably doesn’t work the way he says? That the part behind the LED is milky white and not a shiny reflector? That its beam clearly doesn’t come out parallel to the axis but spreads quite widely? No, I’m sure you already noticed all that.

Next post Previous post