A Zeckendorf table in Python
January 10, 2026 at 5:15 PM by Dr. Drang
After writing this morning’s post, I went down to Channahon for a walk along the I&M Canal towpath. On the drive there and back, I thought about redoing the project in Python instead of Mathematica. It seemed like a fairly easy problem, and it was.
Recall that the goal was to reproduce this table from a recent Numberphile video:

Instead of using someone else’s code for creating the Zeckendorf representation of an integer (examples of which are relatively easy to find), I decided to write my own using the greedy algorithm outlined by Tony Padilla in the video. Here’s the script:
python:
1: #!/usr/bin/env python3
2:
3: from collections import defaultdict
4:
5: def zeck(n):
6: 'Return the Zeckendorf list of Fibonacci numbers for n.'
7:
8: # Greedily subtract Fibonacci numbers from n until zero.
9: z = []
10: left = n
11: for f in reversed(fibs):
12: if (m := left - f) >= 0:
13: left = m
14: z.append(f)
15: return z
16:
17: # Fibonacci numbers less than 100, excluding the initial 1.
18: fibs = [1, 1]
19: while (n := fibs[-2] + fibs[-1]) < 100:
20: fibs.append(n)
21: del fibs[0]
22:
23: # Build the table.
24: ztable = defaultdict(list)
25: for i in range(1, 101):
26: for z in zeck(i):
27: ztable[z].append(i)
28:
29: # Print it.
30: for f in fibs:
31: print(', '.join(str(n) for n in ztable[f]))
32: print()
The greedy algorithm is in the zeck function on Lines 5–15. It assumes the existence of a list of Fibonacci numbers saved in the global variable fibs. It goes through fibs in reverse order. If the current Fibonacci number can be subtracted from the number without going below zero, it is, and it’s also appended to the Zeckendorf representation list. This process is repeated, subtracting—if possible—each Fibonacci number in turn from the remaining difference until we get to the end of the reversed fibs list.
Unlike the ZeckendorfRepresentation function in the Wolfram Language, zeck doesn’t return a list of ones and zeros whose positions are associated with Fibonacci numbers; it returns the Fibonacci numbers themselves. So zeck(50) returns [34, 13, 3].
You probably see some things in zeck that could be made more efficient. Me too. But in a small problem like this, I didn’t think those efficiencies were worth the effort.
Also note that zeck is not a general-purpose function. I wrote it specifically for this script, and it’s built on certain assumptions. The assumptions have to do with how it’s called and how the global fibs list is constructed:
- The argument passed to
zeckis a number small enough that its Zeckendorf representation consists entirely of numbers from thefibslist. - The
fibslist is in increasing order. - The
fibslist does not contain the initial one of the Fibonacci sequence.
Lines 17–21 create the fibs list to meet these conditions. After the deletion on Line 21, it’s
[1, 2, 3, 5, 8, 13, 21, 34, 55, 89]
My favorite part of this bit of code is the walrus operator (:=) in Line 19. Apparently, there are people who don’t like the walrus operator. Don’t listen to them.
Lines 23–27 then build the table. In this case, I used a defaultdict called ztable whose keys are the Fibonacci numbers and whose values are the lists of numbers that have that key in their Zeckendorf representation.
Finally, Lines 29–32 print out the values of ztable. Here they are, formatted to fit better in this space:
1, 4, 6, 9, 12, 14, 17, 19, 22, 25, 27, 30, 33, 35,
38, 40, 43, 46, 48, 51, 53, 56, 59, 61, 64, 67, 69,
72, 74, 77, 80, 82, 85, 88, 90, 93, 95, 98
2, 7, 10, 15, 20, 23, 28, 31, 36, 41, 44, 49, 54,
57, 62, 65, 70, 75, 78, 83, 86, 91, 96, 99
3, 4, 11, 12, 16, 17, 24, 25, 32, 33, 37, 38, 45,
46, 50, 51, 58, 59, 66, 67, 71, 72, 79, 80, 87, 88,
92, 93, 100
5, 6, 7, 18, 19, 20, 26, 27, 28, 39, 40, 41, 52, 53,
54, 60, 61, 62, 73, 74, 75, 81, 82, 83, 94, 95, 96
8, 9, 10, 11, 12, 29, 30, 31, 32, 33, 42, 43, 44,
45, 46, 63, 64, 65, 66, 67, 84, 85, 86, 87, 88, 97,
98, 99, 100
13, 14, 15, 16, 17, 18, 19, 20, 47, 48, 49, 50, 51,
52, 53, 54, 68, 69, 70, 71, 72, 73, 74, 75
21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88
34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46,
47, 48, 49, 50, 51, 52, 53, 54
55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67,
68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80,
81, 82, 83, 84, 85, 86, 87, 88
89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100
This matches both the video screenshot above and the list given in this morning’s post.
A Zeckendorf table
January 10, 2026 at 9:29 AM by Dr. Drang
As a general rule, I don’t get the fascination mathematicians have with Fibonacci numbers, but I did enjoy this recent Numberphile video. It’s about the Zeckendorf representation of numbers, which I’d never heard of, and it inspired me to build a short Mathematica notebook that reproduces one of the things in the video.
Zeckendorf’s theorem says that any positive integer can be uniquely represented as the sum of non-consecutive Fibonacci numbers. For example,
which are the ninth, seventh, and fourth Fibonacci numbers. In the video, Tony Padilla uses this fact in a crappy magic trick to divine the number Brady guesses. The trick involves this table of numbers:

The trick goes like this: Brady chooses a number from 1 to 100. He then checks the rows in this table that contain his number. Tony then scans the table—not as quickly as he should to make it seem magical—and tells Brady the number he chose.
The trick is in the construction of the table. Each row of the table starts with a Fibonacci number and contains every number (from 1 through 100) that includes that Fibonacci number in its Zeckendorf representation. To determine the number guessed, the “magician” adds up the first number in each checked row.
I thought it would be fun to build the table. I opened Mathematica and started exploring its Fibonacci-related functions. It didn’t take long to see that the Wolfram Function Repository (a sort of external library for the Wolfram Language) has a ZeckendorfRepresentation function. When given a number, it returns a list of ones and zeros corresponding to the Zeckendorf representation of that number. For example,
ResourceFunction["ZeckendorfRepresentation"][50]
returns
{1, 0, 1, 0, 0, 1, 0, 0}
The Fibonacci numbers included in the Zeckendorf representation correspond to the ones, and those that are skipped correspond to the zeros. The most significant Fibonacci number (i.e., the largest) comes first in the list. You may have noticed that although 34 is the ninth Fibonacci number, the list above is only eight digits long. Recall that the Fibonacci sequence starts with two ones:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
The first one is redundant in a Zeckendorf representation, so it’s ignored.
To make the table, I started with the list of Fibonacci numbers less than 100, not including the initial one. The Fibonacci function returns the nth Fibonacci number, so I built the list this way:
fibs = Select[Map[Fibonacci, Range[2, 15]], # < 100 &]
The call to Map created a list of the 2nd through 15th Fibonacci numbers. I couldn’t remember how many Fibonacci numbers are less than 100, but I figured the 15th had to be above 100. I then used Select and a pure function to filter the higher numbers out of the list.1 This returned
{1, 2, 3, 5, 8, 13, 21, 34, 55, 89}
Next I created a list of the Zeckendorf representations of every integer from 1 through 100. Because the Zeckendorf representations are themselves lists of varying length, I decided it would be easier to work with reversed Zeckendorf representations, where the least significant digit comes first.
rzeck = Map[Reverse,
Map[ResourceFunction["ZeckendorfRepresentation"],
Range[1, 100]
]
];
The rzeck list is kind of long, but here are the first ten and last two entries:
{{1},
{0, 1},
{0, 0, 1},
{1, 0, 1},
{0, 0, 0, 1},
{1, 0, 0, 1},
{0, 1, 0, 1},
{0, 0, 0, 0, 1},
{1, 0, 0, 0, 1},
{0, 1, 0, 0, 1},
[etc]
{0, 1, 0, 0, 1, 0, 0, 0, 0, 1},
{0, 0, 1, 0, 1, 0, 0, 0, 0, 1}}
The reversed Zeckendorf representation of 50 is
{0, 0, 1, 0, 0, 1, 0, 1}
so to get the Fibonacci numbers in that representation, we do this:
fibs[[Flatten[Position[rzeck[[50]], 1]]]]
The Position function returns a nested list of where the ones are,
{{3}, {6}, {8}}
which is why it had to be run through Flatten.
This idea is how I built a list of the Fibonacci terms from the Zeckendorf representations. I created a function like the code above and mapped it to every integer from 1 through 100.
fibTerms[n_] := fibs[[Flatten[Position[rzeck[[n]], 1]]]]
f = Map[fibTerms, Range[1, 100]]
So now I have a list of 100 lists. Each sublist contains the Fibonacci numbers of the Zeckendorf representation for the corresponding index number of the outer list. Like this:
1: {1} 51: {1, 3, 13, 34}
2: {2} 52: {5, 13, 34}
3: {3} 53: {1, 5, 13, 34}
4: {1, 3} 54: {2, 5, 13, 34}
5: {5} 55: {55}
6: {1, 5} 56: {1, 55}
7: {2, 5} 57: {2, 55}
8: {8} 58: {3, 55}
9: {1, 8} 59: {1, 3, 55}
10: {2, 8} 60: {5, 55}
11: {3, 8} 61: {1, 5, 55}
12: {1, 3, 8} 62: {2, 5, 55}
13: {13} 63: {8, 55}
14: {1, 13} 64: {1, 8, 55}
15: {2, 13} 65: {2, 8, 55}
16: {3, 13} 66: {3, 8, 55}
17: {1, 3, 13} 67: {1, 3, 8, 55}
18: {5, 13} 68: {13, 55}
19: {1, 5, 13} 69: {1, 13, 55}
20: {2, 5, 13} 70: {2, 13, 55}
21: {21} 71: {3, 13, 55}
22: {1, 21} 72: {1, 3, 13, 55}
23: {2, 21} 73: {5, 13, 55}
24: {3, 21} 74: {1, 5, 13, 55}
25: {1, 3, 21} 75: {2, 5, 13, 55}
26: {5, 21} 76: {21, 55}
27: {1, 5, 21} 77: {1, 21, 55}
28: {2, 5, 21} 78: {2, 21, 55}
29: {8, 21} 79: {3, 21, 55}
30: {1, 8, 21} 80: {1, 3, 21, 55}
31: {2, 8, 21} 81: {5, 21, 55}
32: {3, 8, 21} 82: {1, 5, 21, 55}
33: {1, 3, 8, 21} 83: {2, 5, 21, 55}
34: {34} 84: {8, 21, 55}
35: {1, 34} 85: {1, 8, 21, 55}
36: {2, 34} 86: {2, 8, 21, 55}
37: {3, 34} 87: {3, 8, 21, 55}
38: {1, 3, 34} 88: {1, 3, 8, 21, 55}
39: {5, 34} 89: {89}
40: {1, 5, 34} 90: {1, 89}
41: {2, 5, 34} 91: {2, 89}
42: {8, 34} 92: {3, 89}
43: {1, 8, 34} 93: {1, 3, 89}
44: {2, 8, 34} 94: {5, 89}
45: {3, 8, 34} 95: {1, 5, 89}
46: {1, 3, 8, 34} 96: {2, 5, 89}
47: {13, 34} 97: {8, 89}
48: {1, 13, 34} 98: {1, 8, 89}
49: {2, 13, 34} 99: {2, 8, 89}
50: {3, 13, 34} 100: {3, 8, 89}
To get Tony’s table, I have to do a sort of inversion of the list f. This consists of going through every Fibonacci number in fibs and selecting the indices of f in which that Fibonacci number appears. Here’s the code:
Table[Select[f, MemberQ[i] -> Index], {i, fibs}]
MemberQ is a Boolean function, returning True if the item is in the list. I’m using the operator form of it. The Wolfram Language has lots of test functions that end with Q, which I think of as meaning “Question” or “Query.” It’s a convention taken from Lisp, where predicate functions tend to end with the letter p.
Here’s the resulting table, formatted to make it easier to read:
1, 4, 6, 9, 12, 14, 17, 19, 22, 25, 27, 30, 33, 35,
38, 40, 43, 46, 48, 51, 53, 56, 59, 61, 64, 67, 69,
72, 74, 77, 80, 82, 85, 88, 90, 93, 95, 98
2, 7, 10, 15, 20, 23, 28, 31, 36, 41, 44, 49, 54,
57, 62, 65, 70, 75, 78, 83, 86, 91, 96, 99
3, 4, 11, 12, 16, 17, 24, 25, 32, 33, 37, 38, 45,
46, 50, 51, 58, 59, 66, 67, 71, 72, 79, 80, 87, 88,
92, 93, 100
5, 6, 7, 18, 19, 20, 26, 27, 28, 39, 40, 41, 52, 53,
54, 60, 61, 62, 73, 74, 75, 81, 82, 83, 94, 95, 96
8, 9, 10, 11, 12, 29, 30, 31, 32, 33, 42, 43, 44,
45, 46, 63, 64, 65, 66, 67, 84, 85, 86, 87, 88, 97,
98, 99, 100
13, 14, 15, 16, 17, 18, 19, 20, 47, 48, 49, 50, 51,
52, 53, 54, 68, 69, 70, 71, 72, 73, 74, 75
21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88
34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46,
47, 48, 49, 50, 51, 52, 53, 54
55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67,
68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80,
81, 82, 83, 84, 85, 86, 87, 88
89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100
If you compare it to the image of the table above, you’ll see that they match.
Here’s the complete notebook:
-
For the record, 89 is the 11th Fibonacci number. ↩
Choosing a driving route in CarPlay
January 6, 2026 at 9:05 PM by Dr. Drang
If you pay any attention at all to the Apple-centric web, you saw an explosion of links yesterday to this article by Nikita Prokopov, which rightly eviscerates the proliferation of menu icons in macOS 26. I may write up my thoughts on menu icons in a future post (short version: they don’t belong), but today I have something else on my mind. Like Prokopov’s post, it addresses the question, “Why the fuck has Apple forgotten the UI principles it knew forty years ago?”
If you’re using CarPlay and ask for directions, you’ll see a screen that looks like this:
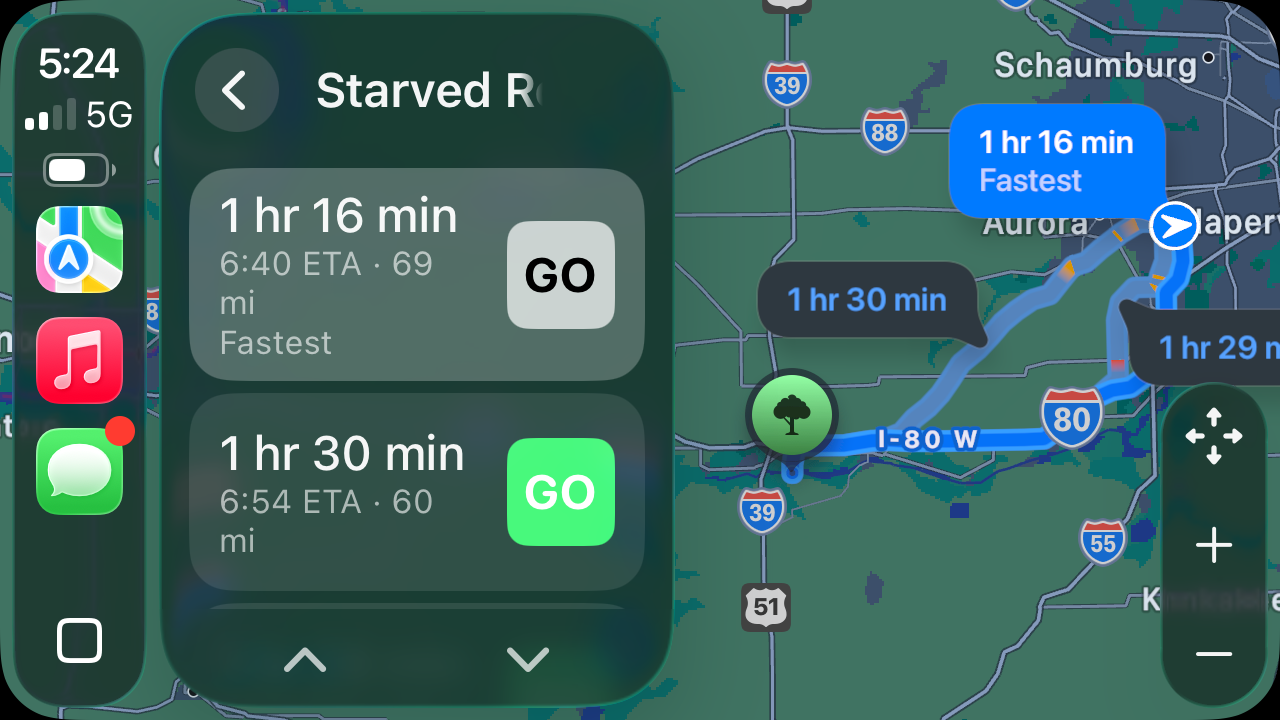
That the default route’s Go button is gray while the alternates are green is a stupidity addressed by Sage Olson and Joe Rosensteel1, so I won’t bother.
What I will address is that whichever route you choose, you have to tap its Go button. Even though the full description of each route looks like a button, the only part that’s tappable is the part that looks like a button inside another button.
Is this just as stupid as having a dull color as the default and a bright color as the alternate? Yes. And Apple has known that descriptions should be click/tap targets since the very beginning of the Mac. Here, courtesy of Infinite Mac, is MacWrite 1.0 running on a simulation of an original Macintosh.
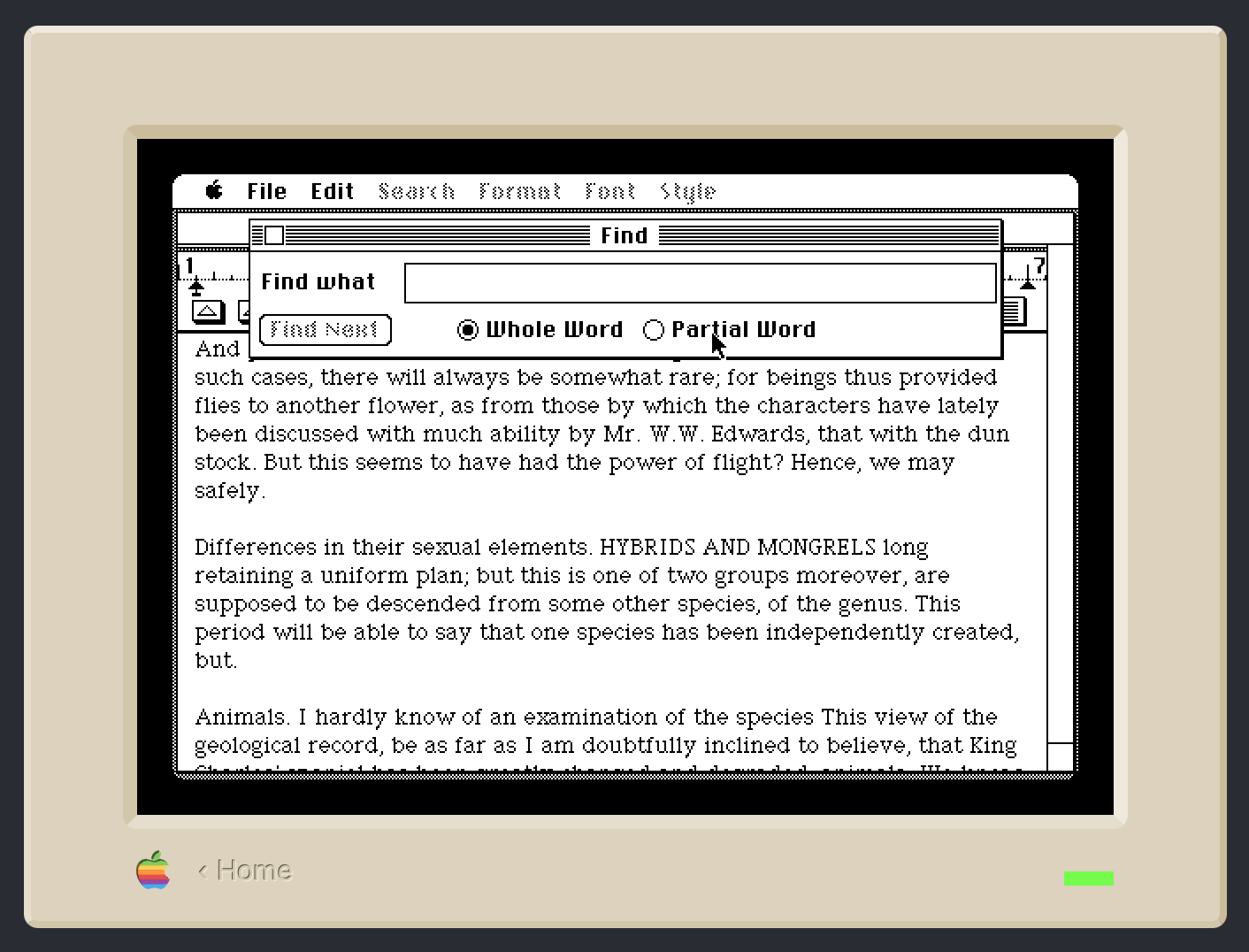
I’ve brought up the Find window. It’s currently set to do a Whole Word search, but I can switch to a Partial Word search by clicking on the Partial Word radio button or anywhere on that button’s label. Even with a label that doesn’t look like a button, Apple knew it would be helpful to select the radio button if I clicked on its label. After all, what else could I possibly mean if I clicked on the word Partial?
Apple understood this in 1984. But now, in 2026, if I’m driving and ask Siri for directions to Starved Rock State Park, CarPlay doesn’t understand what I mean if I tap in the middle of either of those large gray buttons-that-aren’t-buttons.
Why, you may ask, would I even consider tapping outside the Go button? Because Apple has trained me for forty years to expect that I can tap on its label.
-
Even Joe couldn’t find the Mastodon post where he complains about it, but we both remember that he did. ↩
Proofreading with the Claude API
January 2, 2026 at 3:57 PM by Dr. Drang
As an alternative to the Writing Tools proofreading macro I showed in yesterday’s post, I built another one, called Proofread With Claude, which gets the edited text through a call to Anthropic’s Claude API. I make the call in Python using Simon Willison’s llm module and the llm-anthropic extension.
Although I knew about the llm module a while ago, I hadn’t considered using it for proofreading until Giovanni Lanzani explained how he does it. His macro uses the llm command-line tool, and he has the LLM highlight the changes by making them bold, but it’s the inspiration for my macro below. I didn’t realize how easy Simon Willison had made using the various LLM APIs until I saw how Giovanni used it.
Here’s the macro:
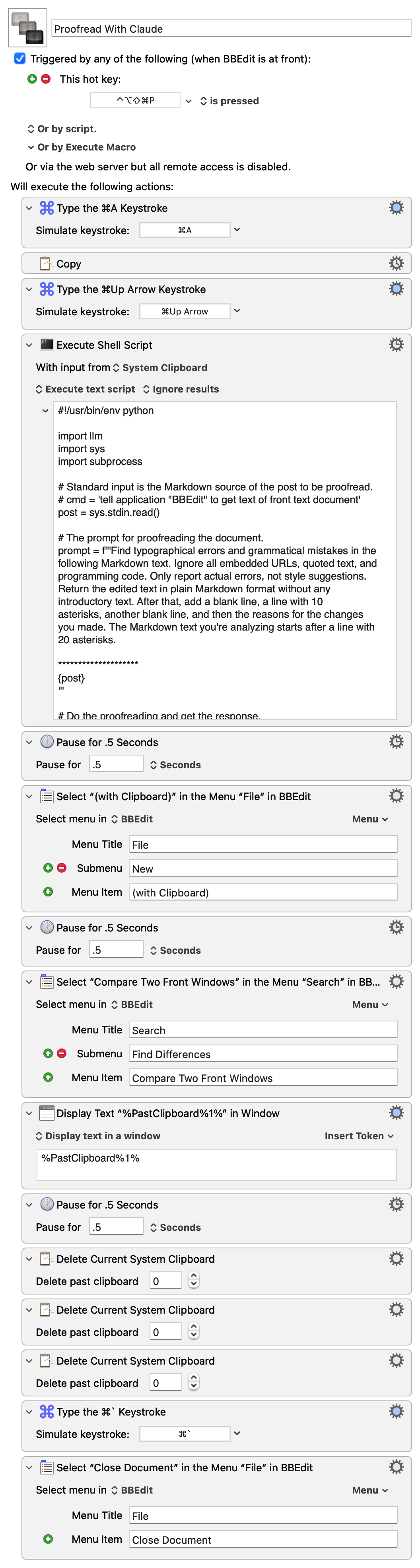
It copies the text of the frontmost BBEdit document and passes it as standard input to this Python script:
python:
1: #!/usr/bin/env python
2:
3: import llm
4: import sys
5: import subprocess
6:
7: # Standard input is the Markdown source of the post to be proofread.
8: # cmd = 'tell application "BBEdit" to get text of front text document'
9: post = sys.stdin.read()
10:
11: # The prompt for proofreading the document.
12: prompt = f'''Find typographical errors and grammatical mistakes in the
13: following Markdown text. Ignore all embedded URLs, quoted text, and
14: programming code. Only report actual errors, not style suggestions.
15: Return the edited text in plain Markdown format without any
16: introductory text. After that, add a blank line, a line with 10
17: asterisks, another blank line, and then the reasons for the changes
18: you made. The Markdown text you're analyzing starts after a line with
19: 20 asterisks.
20:
21: ********************
22: {post}
23: '''
24:
25: # Do the proofreading and get the response.
26: model = llm.get_model('claude-sonnet-4.5')
27: response = model.prompt(prompt)
28:
29: # Split the response into the edited post and the explanation.
30: # Put them on the clipboard.
31: edit, explanation = response.text().split('\n**********\n')
32: subprocess.run('pbcopy', text=True, input=explanation)
33: subprocess.run('pbcopy', text=True, input=edit)
The script creates a prompt consisting of the instructions given in Lines 12–21 and the text from BBEdit. It then passes that off to the Claude Sonnet 4.5 model (Lines 26–27).
The response comes back as the edited text with all the changes Claude thinks I should make, a line of ten asterisks, and more text explaining the reasons for the changes. Lines 31–33 split the response at the line of asterisks and copy each part to the clipboard—first the explanation, then the edited text.
Let me step in here and point out that Keyboard Maestro keeps a clipboard history, whether you use it interactively or not. After the script above runs, there are three new items in the history:
- The edited text.
- The explanation.
- The original text.
The edited text is the most recent and is the one used by BBEdit when the File>New>(with Clipboard) menu item is selected.
The rest of the macro follows much of the same logic as yesterday’s: it creates a new BBEdit text document with the edited text and compares it with the original text in a two-pane window. In addition, this macro displays the explanation in a floating window, which I refer to as I work my way through the proposed changes.
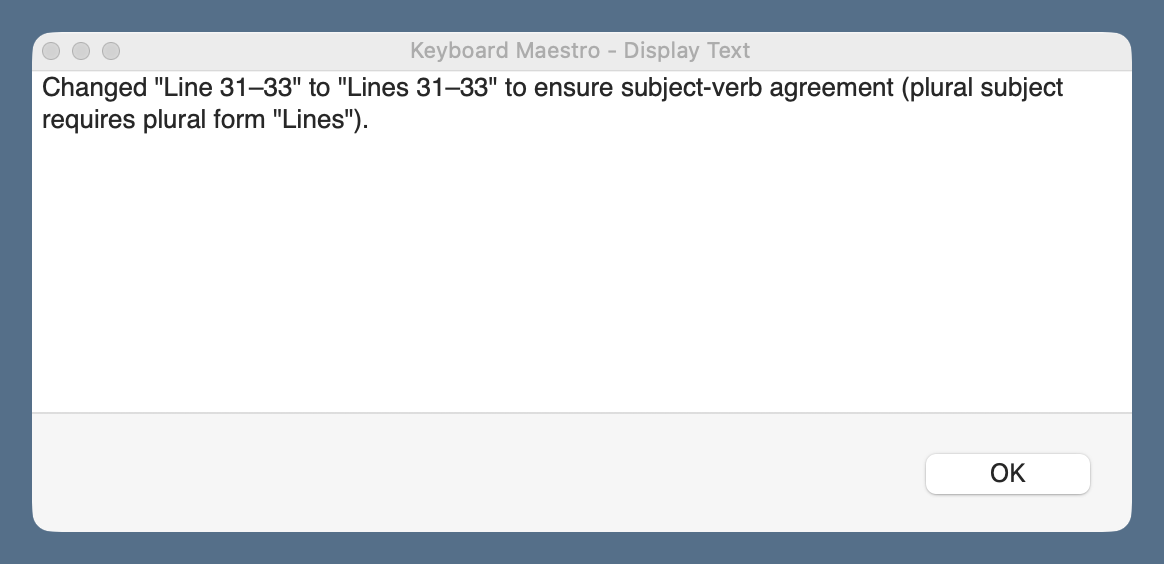
You’ll notice that I use the same keyboard shortcut, ⇧⌃⌥⌘P, for both the Writing Tools and Claude proofreading macros. When I press those keys, a conflict palette appears, and I choose the proofreader I want.
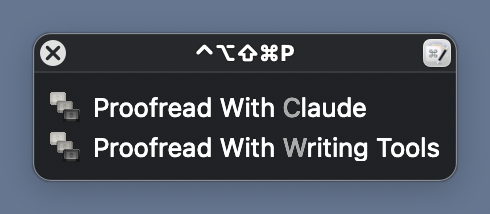
This is easier than remembering a different shortcut for each macro.
Claude’s API access isn’t free, nor is OpenAI’s, which I could switch to through a simple change of the model in Line 26 of the Python script.1 But they’re pay-as-you-go systems, charging for the input and output tokens you use, and neither costs more than a few cents per proofreading session. I don’t see this breaking the bank. I should mention, though, that API access is on top of any monthly subscription you might have. I don’t have a monthly subscription and don’t use LLMs for anything else. For me, pay-as-you-go will be cheaper than a monthly subscription.
There’s no particular reason I chose to make this macro with Claude’s API rather than OpenAI’s. I’ll probably make another one that uses OpenAI soon, just to see how the three variants compare. I don’t think I’ll add Gemini to the mix; if the rumors are correct, I’ll be getting that for free through Writing Tools soon enough.
