And now it’s all this

I just said what I said and it was wrong
Or was taken wrong

There’s nothing you and I won’t do

December 19, 2025 at 9:43 PM by Dr. Drang

I’ve talked about area moments of inertia in the past couple of posts. Today, thanks to Phil Plait, resident astronomer at Scientific American, I have an excuse to talk about mass moments of inertia, the kind you learned about in first semester physics class.

Plait’s article today takes on the Modern English song “I Melt with You” and looks into the energy it would take to stop the world.¹ By “stopping,” he initially assumes that means stopping the rotation of the Earth about its axis. He gives the value, $2\times {10}^{29}\mathrm{j}\mathrm{o}\mathrm{u}\mathrm{l}\mathrm{e}\mathrm{s}$, but doesn’t explain how he calculated that number. Kind of disappointing for SciAm and definitely not acceptable here at ANIAT. Especially since the calculation is easy.

The kinetic energy of a rotating body is

$$\frac{1}{2}I{\omega }^2$$

where $I$ is the mass moment of inertia of the body about its axis of rotation and $\omega$ is its rotational speed.

The value of $I$ is kind of tricky because, as Plait points out, the Earth’s density varies with depth. But we can make an initial estimate by assuming the Earth is a sphere of uniform density. The moment of inertia for that kind of body is

$$I=\frac{2}{5}m{r}^2$$

We get the mass and (average) radius of the Earth from the sadly defunct NASA Earth Fact Sheet, currently available through the Internet Archive. The mass is $5.9722\times {10}^{24}\mathrm{k}\mathrm{g}$ and the mean radius is $6371\mathrm{k}\mathrm{m}$. That gives us a moment of inertia of

$$I=\frac{2}{5}(5.9722\times {10}^{24}\mathrm{k}\mathrm{g}){(6.371\times {10}^6\mathrm{m})}^2=9.6964\times {10}^{37}\mathrm{k}\mathrm{g}{\mathrm{m}}^{\mathrm{2}}$$

Relative to the stars, the Earth rotates once every $23.9345$ hours (that’s the “sidereal rotation period” on the Fact Sheet), so the rotational speed is

$$\omega =\frac{2\pi }{(23.9345\times 60\times 60)\mathrm{s}}=7.29211\times {10}^{-5}{\mathrm{s}}^{\mathrm{-}\mathrm{1}}$$

Putting these together, we get a kinetic energy of

$$\frac{1}{2}(9.6964\times {10}^{37}\mathrm{k}\mathrm{g}{\mathrm{m}}^{\mathrm{2}}){(7.29211\times {10}^{-5}{\mathrm{s}}^{\mathrm{-}\mathrm{1}})}^2=2.578\times {10}^{29}\mathrm{J}$$

This is higher than Plait’s value, but he may have rounded down because he knew the density of the Earth is higher near the center. Also, I suspect he was mostly after an order-of-magnitude answer.

I found a better estimate of $I$ on this page from Eric Weisstein’s World of Science site. It was determined by Kurt Lambeck to be

$$I=8.034\times {10}^{37}\mathrm{k}\mathrm{g}{\mathrm{m}}^{\mathrm{2}}$$

(Lambeck’s book came out just a couple of years before “I Melt with You,” which I’m pretty sure is a coincidence.)

Using this value, we get a rotational kinetic energy of

$$\frac{1}{2}(8.034\times {10}^{37}\mathrm{k}\mathrm{g}{\mathrm{m}}^{\mathrm{2}}){(7.29211\times {10}^{-5}{\mathrm{s}}^{\mathrm{-}\mathrm{1}})}^2=2.136\times {10}^{29}\mathrm{J}$$

which is a better match for Plait’s energy value.

Plait also considers another interpretation of “I’ll stop the world”: stopping the Earth in its orbit. I won’t get into the details of this, first because it doesn’t involve the moment of inertia, and second because stopping the Earth this way would have it fall into the Sun. Not much doubt about melting in that case.

---

Axial vs. bending stiffness

December 19, 2025 at 12:02 PM by Dr. Drang

At the end of yesterday’s post, I mentioned that axial deformations in framework members are typically two orders of magnitude less than the lateral (bending) deformations. It’s easy to see why.

Consider a column with length $L$, cross-sectional area $A$, and moment of inertia $I$. We’ll calculate the tip deflection of this column under two loads of the same magnitude, $P$: an axial compression load and a horizontal load to the right.

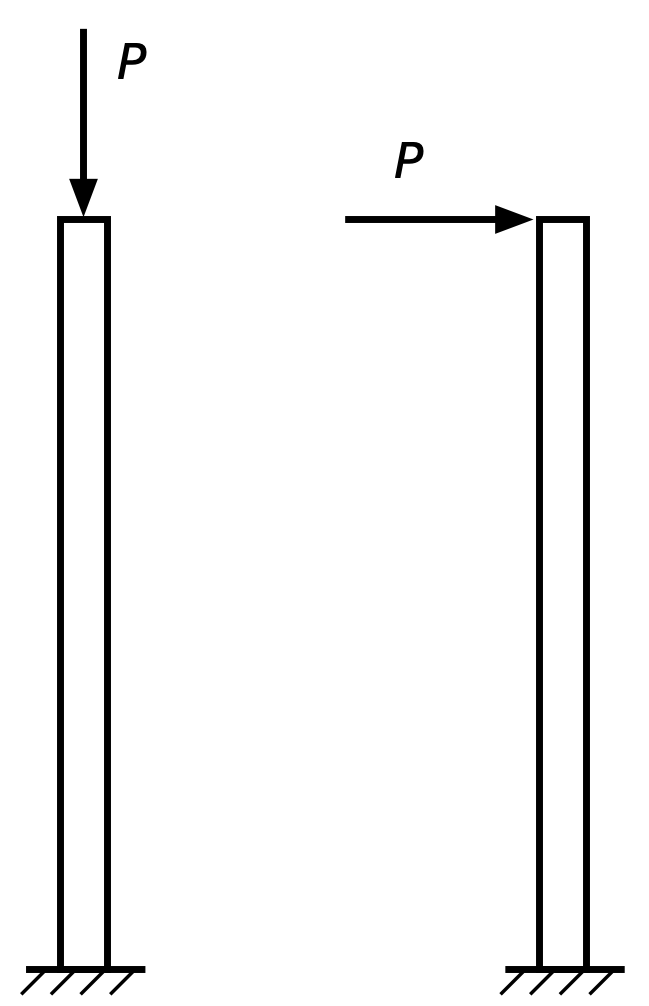
Under the compression load, the tip of the column will move down by

$$\frac{PL}{EA}$$

Under the horizontal load, the tip will move to the right by

$$\frac{P{L}^3}{3EI}$$

The ratio of lateral deflection to axial deflection is therefore

$$\frac{1}{3}\frac{A{L}^2}{I}$$

When calculating buckling loads of columns, it’s often useful to consider the radius of gyration, $r$, which is defined this way:

$$I=A{r}^2\Rightarrow r=\sqrt{\frac{I}{A}}$$

We’re not doing a buckling calculation here, but we can use the radius of gyration to help us get a sense of the deflection ratio, which we can rewrite as

$$\frac{1}{3}{\left(\frac{L}{r}\right)}^2$$

The radius of gyration is some fraction of a characteristic dimension of the cross-section. For example, if the cross-section is a square with side length $b$, the area is $b^2$ and the moment of inertia is $b^4/12$, so

$$r=\sqrt{\frac{b^4/12}{b^2}}=\frac{b}{2\sqrt{3}}\approx 0.289b$$

In typical structures, the stick-like members—beams, columns, braces, etc.—tend to be long and thin, with aspect ratios of about 10. The deflection ratio is roughly the square of the aspect ratio, so lateral deflections are typically two orders of magnitude greater than axial deflections. That’s why it’s common to ignore the axial deflections in analyses like yesterday’s.

This doesn’t mean axial deflections can always be ignored. In tall buildings, the columns carry the weight of all the floors above them, and column shortening has to be accounted for, especially in the lower floors. Also, when using modern numerical techniques for structural analysis, there’s basically no extra work involved in calculating the axial deflections along with the bending deflections, so the axial deflections pop out of the computer as a matter of course.

---

Frame sidesway again

December 18, 2025 at 11:38 AM by Dr. Drang

I’ve been meaning to follow up on the “sense of structure” post I wrote just after Thanksgiving. I don’t have anything profound to say, but I did want to give complete solutions for both the off-center vertical load problem and the horizontal load problem.

First, though, I want to mention a nice email conversation I had with Karl Hoitsma, proprietor of the Mathpax blog. He pointed me to this post of his from a few years ago in which he describes being asked essentially the same frame sidesway question I was. The only real differences were that his oral exam was about five years after mine and that he was at Texas A&M instead of U of I. Oh, and he hadn’t been prepped for the question.

In that post, Karl gives a few solutions to the problem, which I found fun to go through. I had already solved the horizontal load problem for a simpler frame, and it was interesting to compare our approaches to the problem. As I’ve been trying to get better at Mathematica, I decided to do the off-center load problem and redo the horizontal load problem using the Wolfram Language. I won’t go through the code here, just the results.

Let’s start with the simpler problem: a portal frame with fixed column bases in which the beam and columns are identical in both cross-section and length.

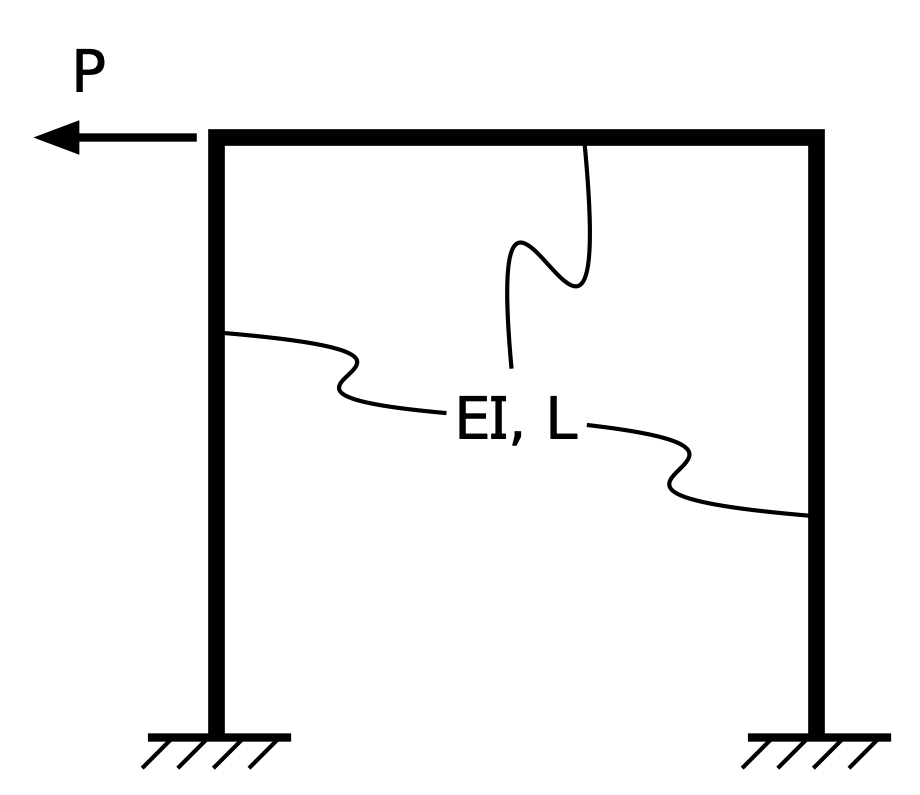
$E$ is the modulus of elasticity of the material, and $I$ is the moment of inertia of the cross-section.¹

This is a statically indeterminate system. You cannot determine the reactions at the bases of the columns through statics alone; you have to account for the stiffnesses of the members. But once you’ve done that, the reactions are these:

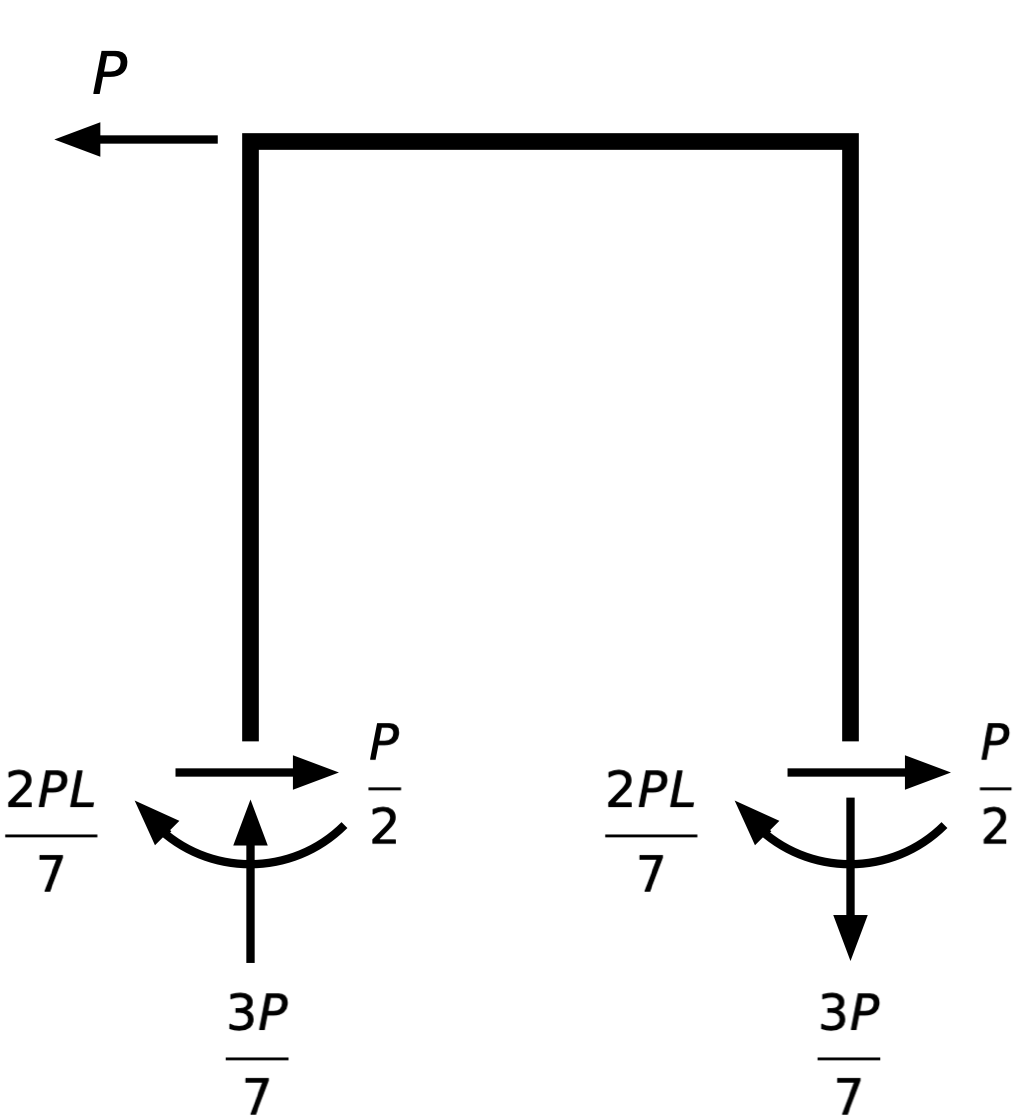
It’s a decent exercise to confirm that these reactions are in equilibrium. It should be immediately obvious that the horizontal and vertical forces are in balance. It takes only a little more effort to show that the clockwise and counter-clockwise moments about any point are also in balance. (As a practical matter, I’d choose the base of one of the columns to take moments about, as that eliminates three of the forces from the equation.)

What I really wanted to show was the deflected shape of the frame under this loading. If you recall from that earlier post, I drew a deflected shape in which the left half of the beam goes up and the right half goes down. Knowing this was key to using reciprocity to determine which way the frame sways when it’s subjected to an off-center vertical load. Here’s the deflected shape plotted from a formal solution instead of just drawn on the basis of my sense of the structure’s behavior:

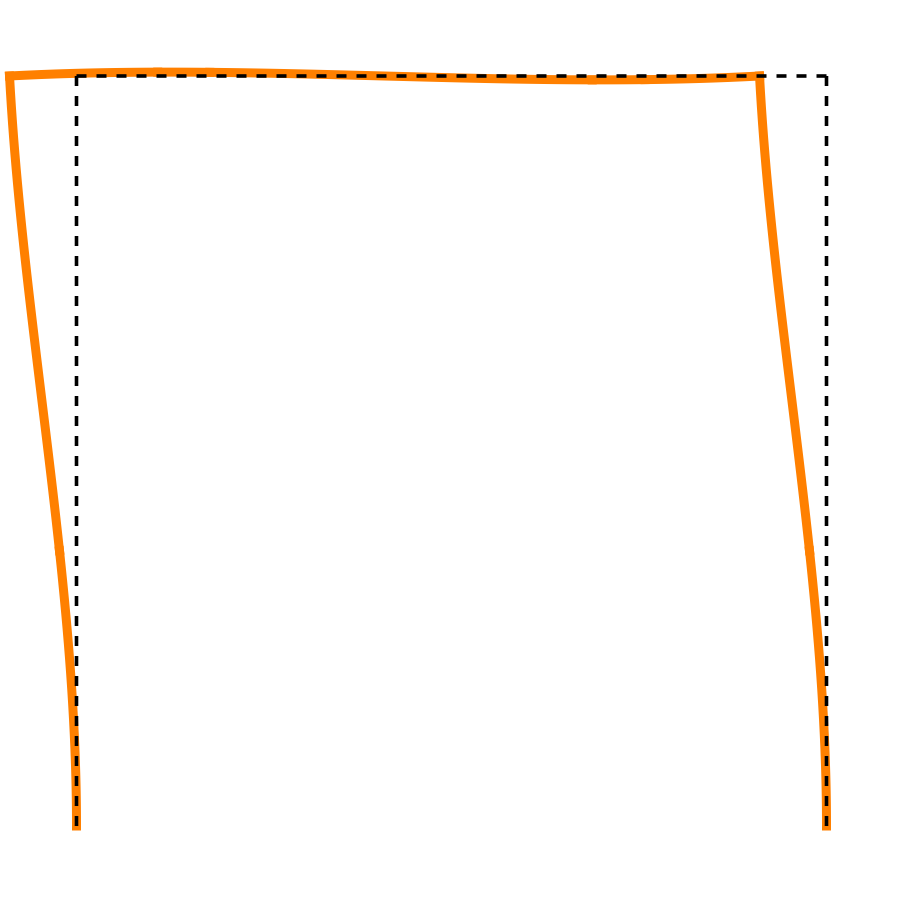
The leftward displacement at the top of each column is

$$\mathrm{\Delta }=\frac{5P{L}^3}{84EI}$$

and the counter-clockwise rotation at the top of each column is

$$\theta =\frac{P{L}^2}{28EI}$$

It’s the CCW rotation that lifts the left half of the beam upward and pushes the right half downward. As you can see, though, the vertical deflection of the beam is pretty small compared to the horizontal deflection of the columns.

A note on units: In these equations, $P$ has units of force, $L$ has units of length, $E$ has units of force per length squared, and $I$ has units of length to the fourth power. So $\mathrm{\Delta }$ has units of length, as expected, and $\theta$ is a pure number, which means we’re getting the rotation in radians.

OK, now let’s look at the frame with a downward off-center load:

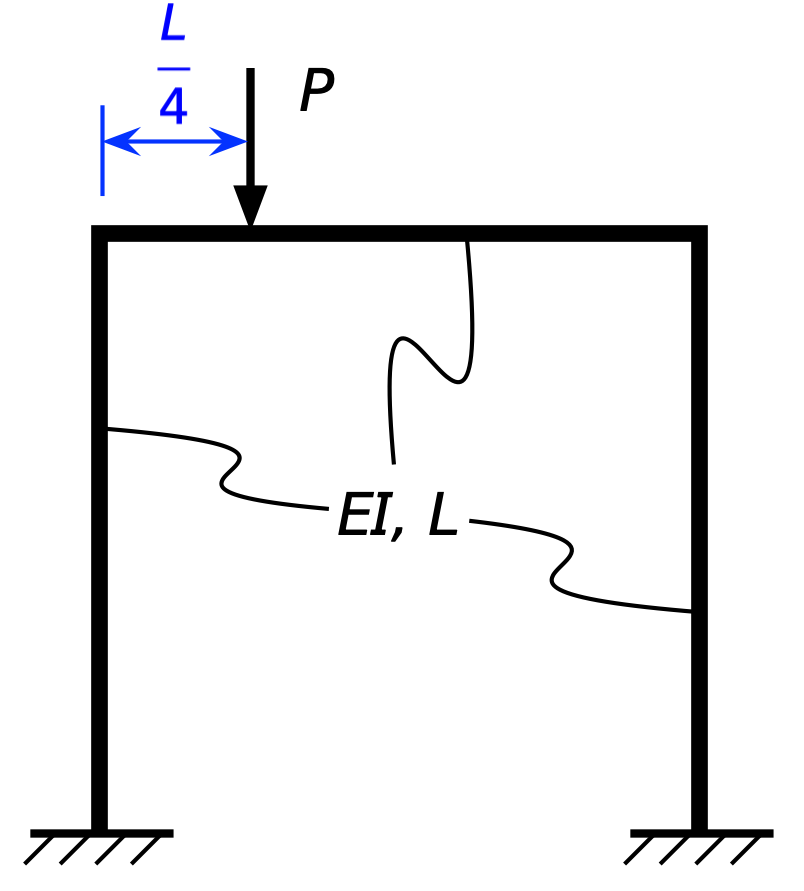
I’ve put the load at the quarter point of the beam for convenience, but it doesn’t matter where it is as long as it’s to the left of the centerline. Here are the reactions:

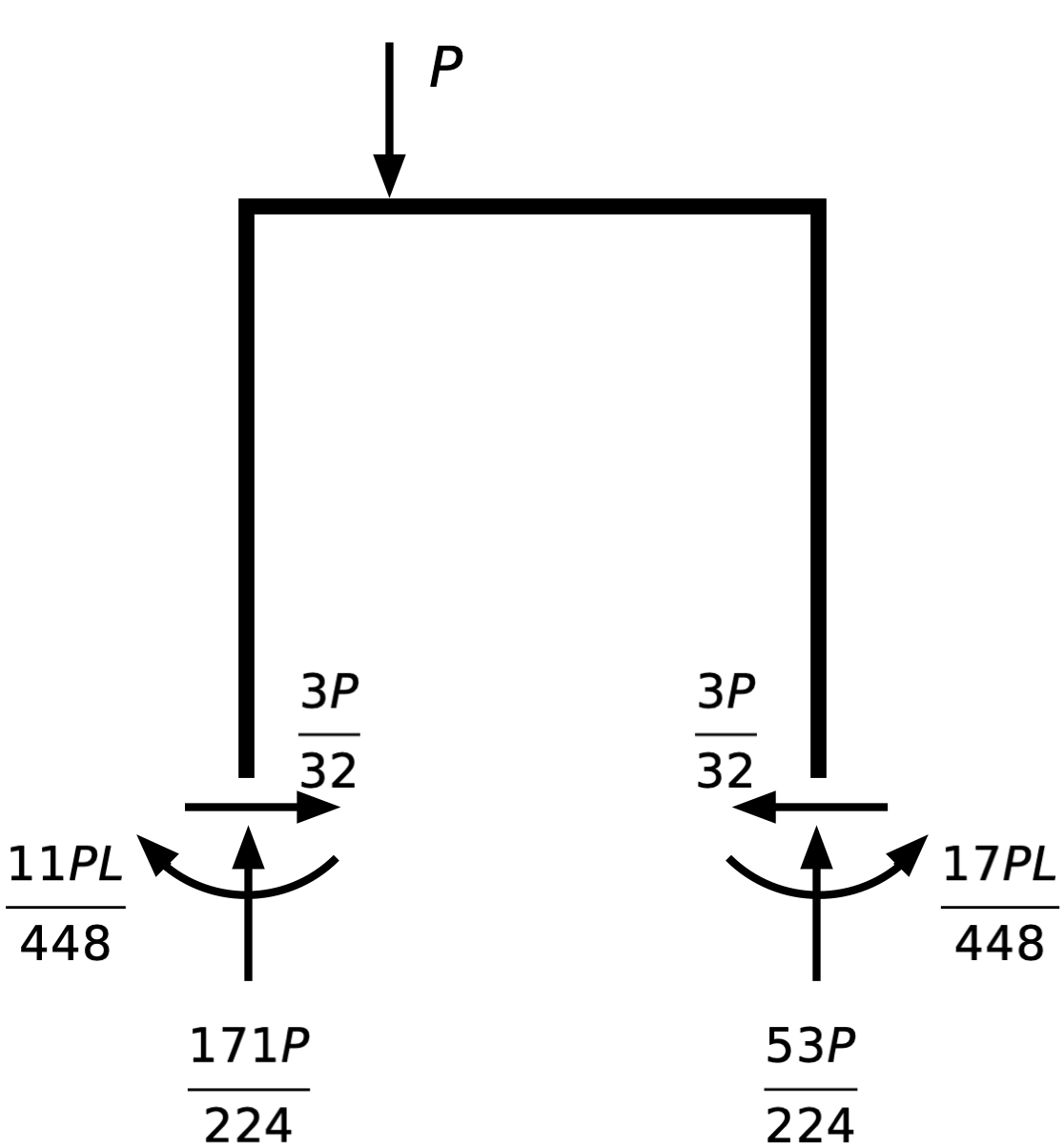
Again, you can confirm that these forces and moments are in equilibrium. Here’s the deflected shape:

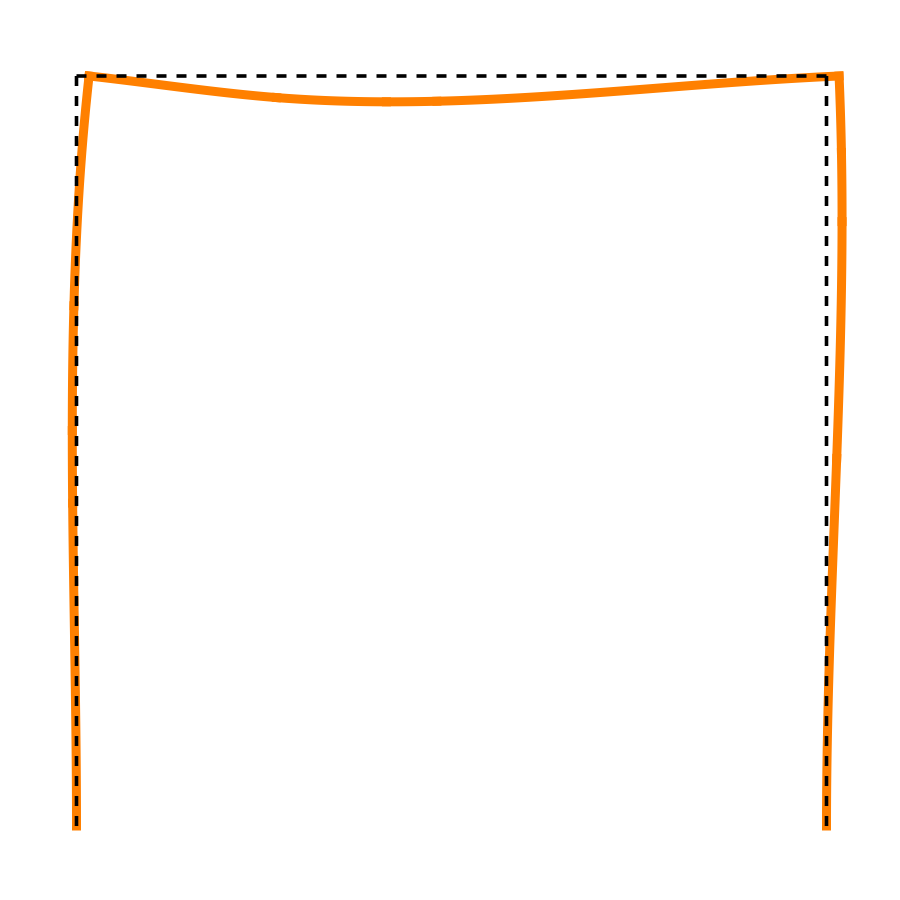
For this loading, the leftward displacement at the top of each column is

$$\mathrm{\Delta }=-\frac{3P{L}^3}{896EI}$$

The minus sign means the displacement is actually to the right, which matches what we figured out a few weeks ago. Now we have the magnitude in addition to the direction.

As I said above, I don’t want to go through the details of the code that got me to these answers, but if you’re interested, you can see it using the following Wolfram Cloud links:

• Portal frame with horizontal load.
• Portal frame with off-center vertical load.

I should mention that in both of these analyses I’m ignoring the axial deformation of the members. This is a common practice in frame analysis, as axial deformations are typically about two orders of magnitude less than lateral deformations. Leaving out the axial terms cuts out a lot of complexity in symbolic solutions like this while retaining good accuracy.

---

Be careful where you click

December 11, 2025 at 10:24 AM by Dr. Drang

I ran into an example of especially bad design on a web page yesterday. Not “how it looks” design; “how it works” design.

Here’s an excerpt from an online payment page:

Looks straightforward, right? Just click in the field, type in the amount to pay, and off you go. But unlike almost every other example you’ll see nowadays, this field doesn’t automatically select its dummy contents when you click in it. So what you type does not replace the dummy contents. Here’s a video showing what can happen.

There are three interactions in the video.

1. I clicked to the right of the “$0.00” default amount and typed “12345.” You can see the zeros disappear as I type, and the amount at the end is $123.45. Let’s assume this is what I wanted to enter.
2. I clicked just to the right of the decimal point and typed “12345.” The cursor first jumps to the beginning of the amount. After I type the “1,” it jumps to the end, and the “2345” fills in from the right. But two of the zeros never disappear, and the amount at the end is $10,023.45.
3. I clicked just to the right of the dollar sign and typed “12345.” After I type “123,” the cursor jumps to the end and the “45” fills in from the right. None of the zeros disappear, and the amount at the end is $123,000.45.

I want to emphasize that I never moved the cursor myself after the initial click in the field. All I did was type.

As you might guess, I discovered this when I nearly made an enormous overpayment.

It’s true that a standard HTML <input type="text" /> form field with a value attribute will put the cursor where you click, so a user could screw up the entry in that kind of field, too. But the value attribute is meant to be a default, a common legitimate entry. No one ever goes online to pay $0.00. A more appropriate pure HTML solution would be to use the placeholder attribute, which puts gray text in the field to suggest what the field is for. As soon as you start typing in such a field, the placeholder text disappears.

For the designers of this website, though, standard HTML just wasn’t good enough. They wanted to show off their elite JavaScript skills to keep the dollar sign and decimal point in place and add commas as the user types. In the process, they created a field in which the cursor jumps around haphazardly and the user can easily create a mistaken payment.

Am I the only user who’s noticed this? Impossible.¹ But we’ve gotten so used to crap like this that we just sigh, figure out how to fix things on our end, and move on with our lives. I did point this problem out to the vendor, who was surprised to hear it, but payment processing is a service they buy from someone else. It’s unlikely that the people responsible for the poor user interface will ever be told to fix it.

---

Newer posts Older posts

Site search

Meta

• drdrang at leancrew
• Blog archive
• RSS feed
• JSON feed
• Mastodon
• GitHub repositories

Recent posts

Credits

This work is licensed under a Creative Commons Attribution-Share Alike 3.0 Unported License.

© 2005–2026, Dr. Drang