SciAm clock puzzle
October 15, 2025 at 5:10 PM by Dr. Drang
Scientific American published a clock puzzle a couple of weeks ago that I finally got around to looking at today. It wasn’t hard, but I’m less interested in the solution than in a very small discrepancy I found. Finding discrepancies was a big part of my job, so it was nice to see that I still can.
Before we go any further, you should know there will be spoilers—there’s no way around that. So if you want to solve it on your own, stop here and click the link in the previous paragraph.
The puzzle concerns this clock face:
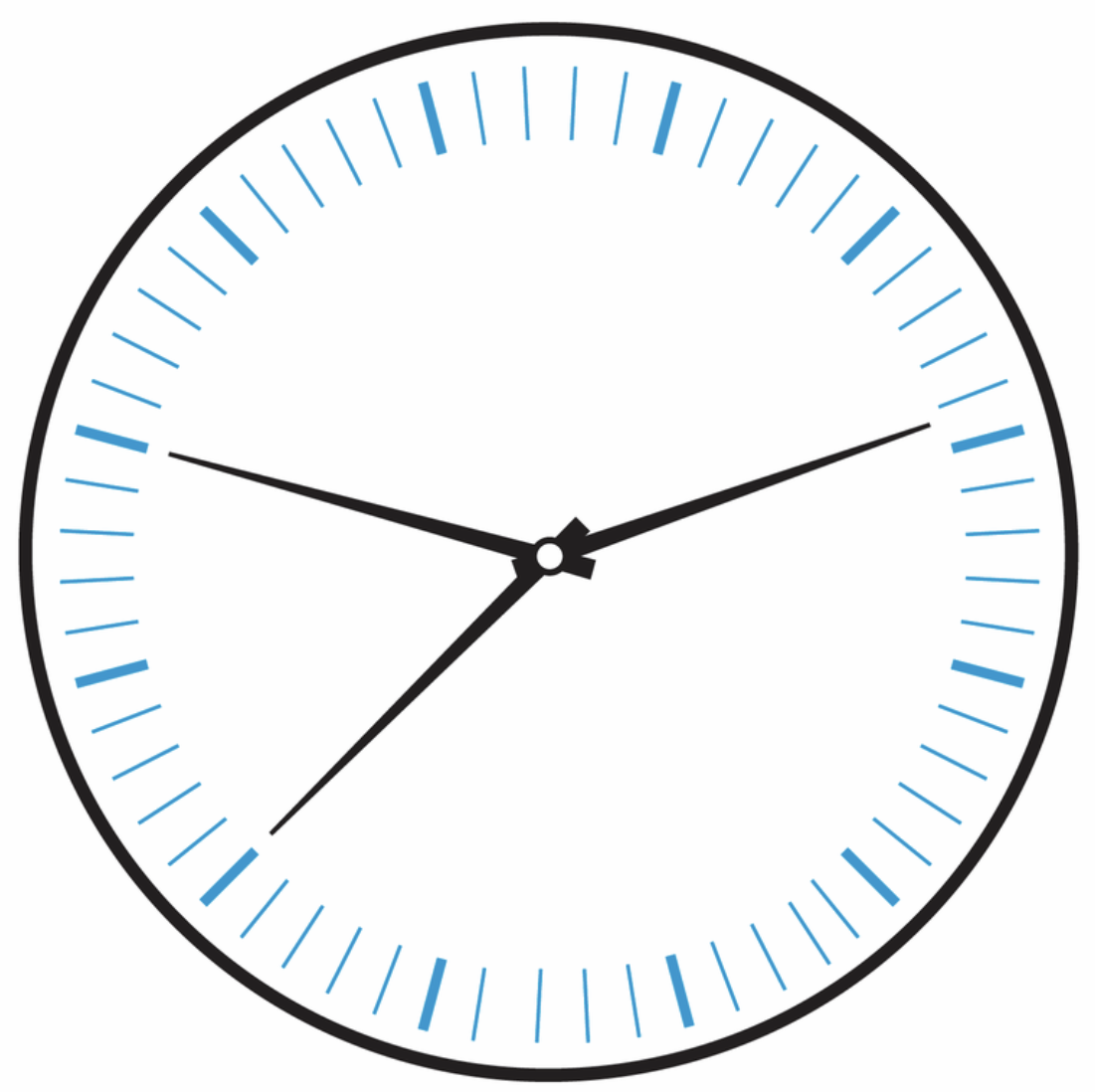
The hour, minute, and second hands are all the same size, there are no numerals, and the clock has been rotated. Your job is to determine the time. I’m going to add some blank space here so people who want to work out the answer don’t accidentally see it.
OK, the answer is 4:50:00, and what bothered me was the position of the hour hand. I thought it was too close to the 5 o’clock tick. Fifty minutes is five-sixths of an hour, which means the hour hand should be
thin minute ticks past the bold 4 tick. Doesn’t it look a little further than that to you? Somewhat more than one-sixth of the way from the thin tick to the thick one?
So I took a screenshot of the clock face and imported it into OmniGraffle. I rotated the face 75° so the second hand is pointing straight up. Then I started drawing lines on the face.
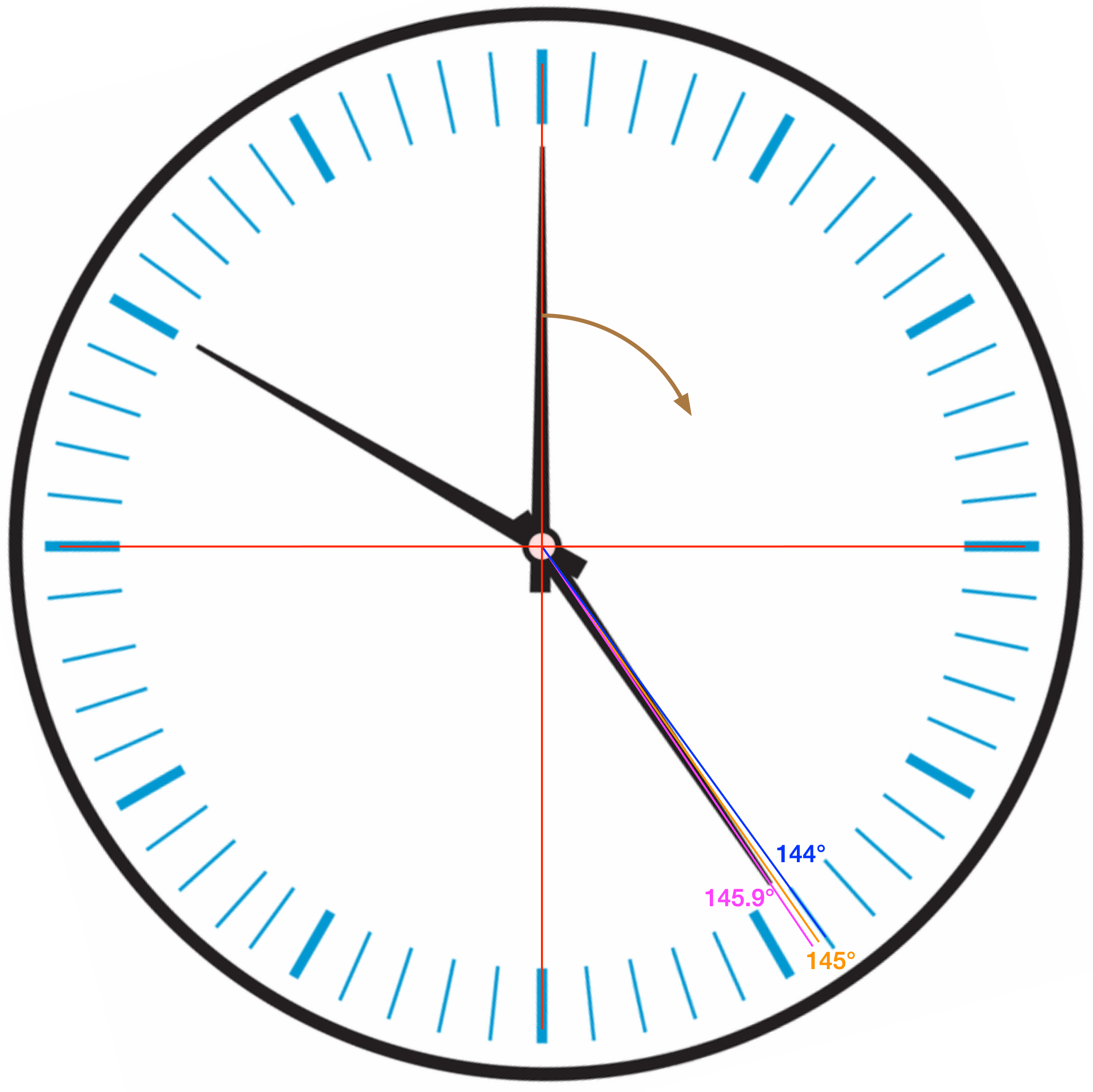
First, I drew horizontal and vertical lines in red to make sure the 75° rotation was correct. It was. Then I added an orange line where I thought the hour hand should be. The hour hand moves 30° every hour and 5° every 10 minutes, so the hour hand should be
clockwise from the 12:00 position. It was definitely not aligned with the hour hand (I’ll show you a zoomed-in view in a minute). To further insure I had the clock face oriented properly, I then drew a blue line at 144°, which is where the 24-minute tick mark should be.1 They lined up well.
Finally, I drew a magenta line at 146°. That was a little off from the hour hand, so I adjusted it down to 145.9°. Here’s the zoomed-in view so you can see where all these lines are:
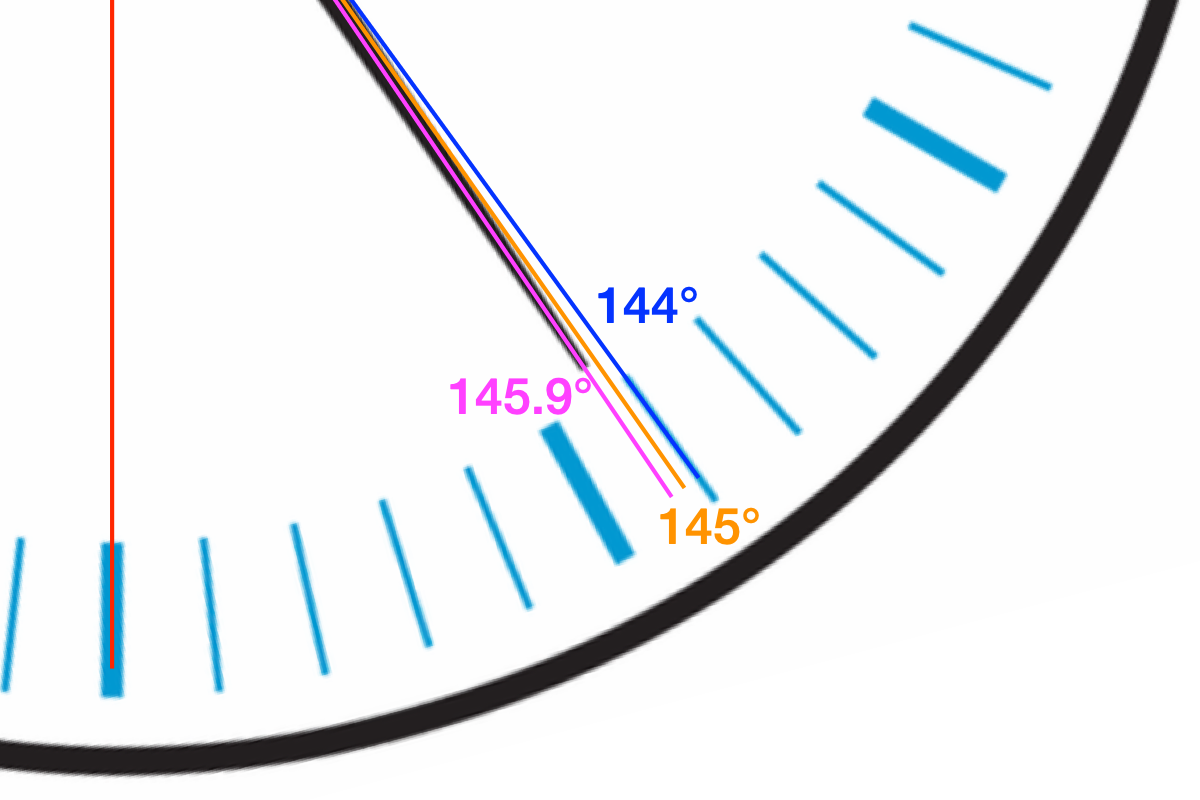
So yes, the hour hand is a little off, nearly twice as far from the 24-minute tick as it should be. I can still find discrepancies, whether there’s any value in it or not.
I’ll leave it to you to decide whether I would have written this post if it had turned out I was wrong.
Update 16 Oct 2025 10:09 AM
Andy Napper, via Mastodon, pointed me to the original article with this puzzle. It’s in Spektrum magazine, but you don’t have to read German to see what Andy saw:
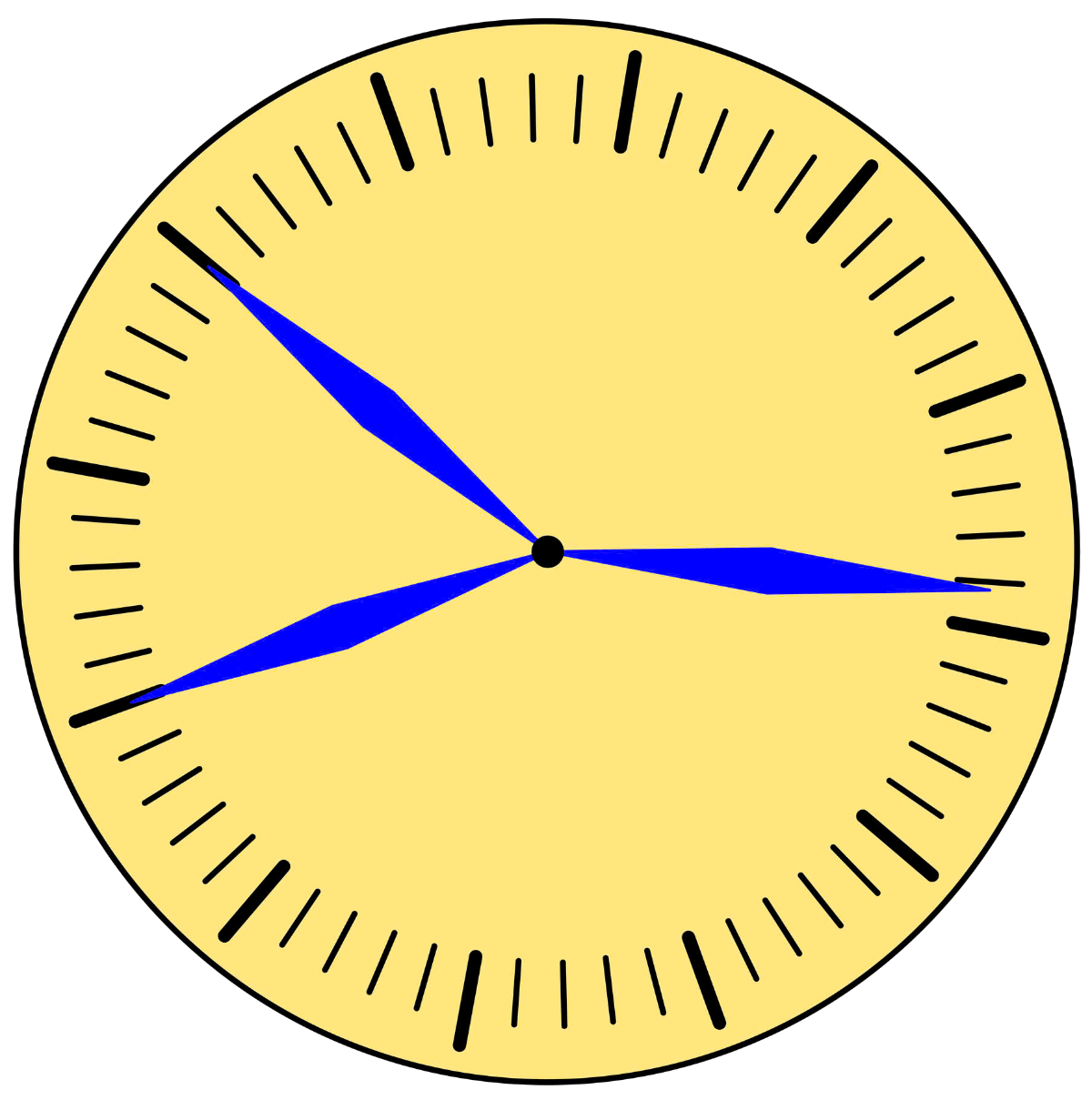
The Spektrum clock face has the hour hand at what looks like exactly the right angle. I would make a joke here about German precision and American sloppiness, but after looking again I see that the minute and second hands in the Spektrum clock aren’t lined up as well with the ticks as they are in the SciAm clock. Too bad.
-
Minute ticks are 6° apart, so 24 minutes is 144° clockwise from straight up. ↩
Markdown link scripts for BBEdit
October 14, 2025 at 5:49 PM by Dr. Drang
A few weeks ago, I mentioned in a footnote that I have a script that takes a URL on the clipboard and makes a Markdown reference-style link in BBEdit. Actually, I have several link-making scripts for BBEdit. I’ve written about some of them already (including very long ago), but never about all of them. Buckle up.
The BBEdit support folder and packages
My linking scripts are all accessible via the Blogging submenu of BBEdit’s Scripts menu.1
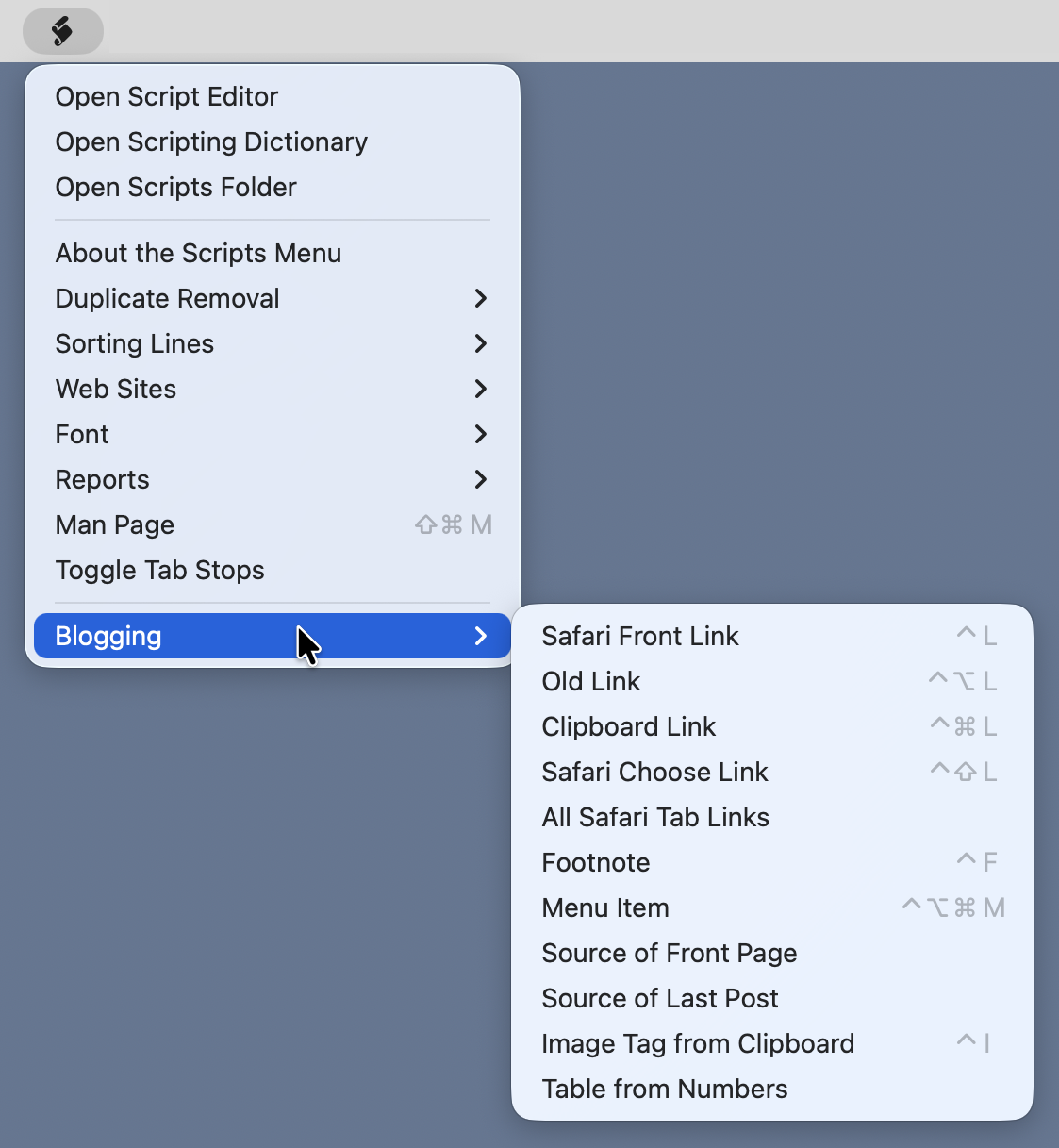
As you can see, I have several blogging scripts, but we’ll focus on just the linking scripts here.
The submenu indicates that the scripts are in the Blogging package, or bundle, which I created to keep all my BBEdit blogging tools in one spot. Rather than trying to explain in words how packages are organized in the BBEdit support folder hierarchy, I’ll show you how I have things arranged:
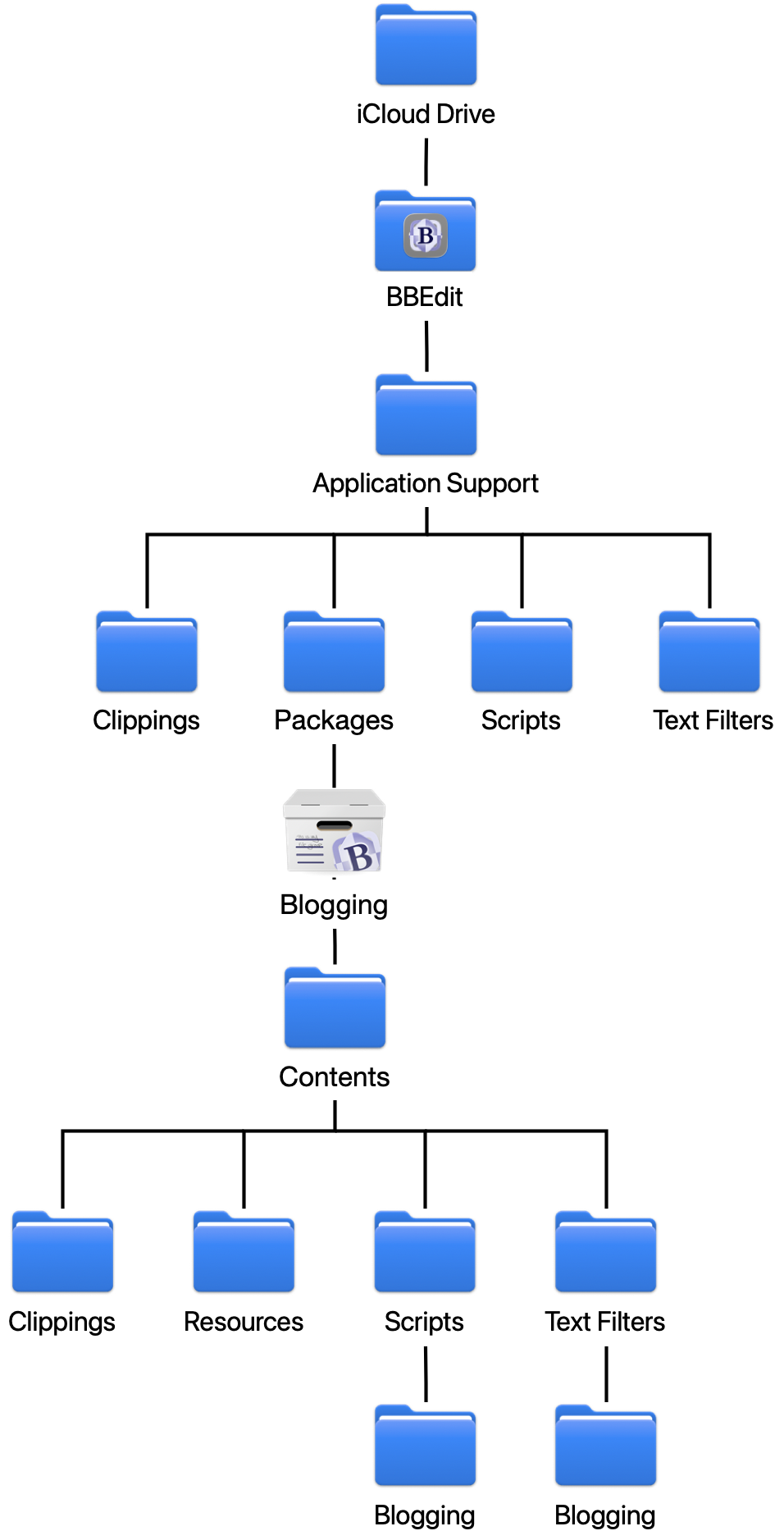
As you can see, I have them set up in iCloud Drive. They can also be in your Dropbox folder or, if you have no need to share configurations across two or more computers, in ~/Library/Application Support/BBEdit. Full instructions on where and how to set up an application support folder can be found in the BBEdit User Manual.
The funny-looking icon labeled Blogging is the package of interest. For linking, there are two utility scripts in the Resources subfolder and five AppleScripts in the Scripts/Blogging subfolder.
Reference link background
As you can see in the Markdown documentation, there are two kinds of links: inline and reference. Inline links look like this:
the [Markdown documentation](https://daringfireball.net/projects/markdown/syntax#link)
where the text that will become the link is enclosed in brackets and the URL is enclosed in parentheses. Reference links look like this:
the [Markdown documentation][1]
where the link text in brackets is followed by a reference, also in brackets. Somewhere else in the file—I put them at the bottom—is the reference again, followed by a colon and the URL:
[1]: https://daringfireball.net/projects/markdown/syntax#link
I’m showing the references as numbers because that’s what I use, but the reference string can be anything.
All of my scripts make reference links, incrementing the reference number as more are added.
Utility scripts
The Blogging package’s utility scripts are saved in its Resources subfolder. Two of them are used to make reference links: nextreflink and getreflink.
Because I use numbers in my reference links, new links need to know what the last reference number was so they can increment it. The nextreflink script figures out what the highest existing reference number is and returns the next integer.
python:
1: #!/usr/bin/env python3
2:
3: import sys
4: import re
5:
6: text = sys.stdin.read()
7: reflinks = re.findall(r'^\[(\d+)\]: ', text, re.MULTILINE)
8: if len(reflinks) == 0:
9: print(1)
10: else:
11: print(max(int(x) for x in reflinks) + 1)
It assumes the Markdown source of the file I’m working on will be fed to it via standard input. It uses the regular expression on Line 7 to find all the reference links in the file and collects them in the list reflinks. Because the regex has just one capturing group, the findall function returns a list of just that group. If there are no reference links in the file yet, Line 9 returns 1; otherwise, Line 11 determines the maximum reference number and adds 1 to it.
As we’ll see in the next section, nextreflink is used by all the link-making scripts that create new links. But one of the scripts, Old Link, doesn’t make a new link; it presents me with a list of all the links already in the file so I can choose one to use again. The utility script getreflink does that:
python:
1: #!/usr/bin/env python3
2:
3: import sys
4: import re
5: import subprocess
6:
7: # Utility function for shortening text.
8: def shorten(str, n):
9: 'Truncate str to no more than n chars'
10: return str if len(str) <= n else str[:n-1] + '…'
11:
12: # Read in the buffer and collect all the reference links.
13: text = sys.stdin.read()
14: refRE = re.compile(r'^\[(\d+)\]: +([a-z]+://)?(.+)$', re.MULTILINE)
15: refs = refRE.findall(text)
16:
17: # Create an AppleScript to ask the user for the link
18: choices = [ shorten(x[2], 100) for x in refs ]
19: choiceString = tString = '{"' + '", "'.join(choices) + '"}'
20: firstChoice = f'{{"{choices[0]}"}}'
21: cmd = f'''
22: set theLinks to {choiceString}
23: tell application "System Events"
24: activate
25: choose from list theLinks with title "Choose Reference Link" default items {firstChoice}
26: end tell
27: get item 1 of result
28: '''
29:
30: # Run the AppleScript
31: osa = subprocess.run(['osascript', '-'], input=cmd, text=True, capture_output=True)
32: if osa.returncode == 0:
33: choice = osa.stdout.rstrip()
34: else:
35: sys.exit()
36:
37: # Get the reference number
38: idx = choices.index(choice)
39: print(refs[idx][0])
This one’s got a lot of pieces. The first step, as in nextreflink, is to go through standard input and collect all the reference links. That’s done in Lines 13–15. The findall here generates a list of tuples. Each tuple consists of the reference number, the URL scheme (typically https://), and then everything after that. The third item is what we’ll use to make the selection.
Before we look at the rest of the code, here’s the prompt presented to the user. The URL is selected from the given list.
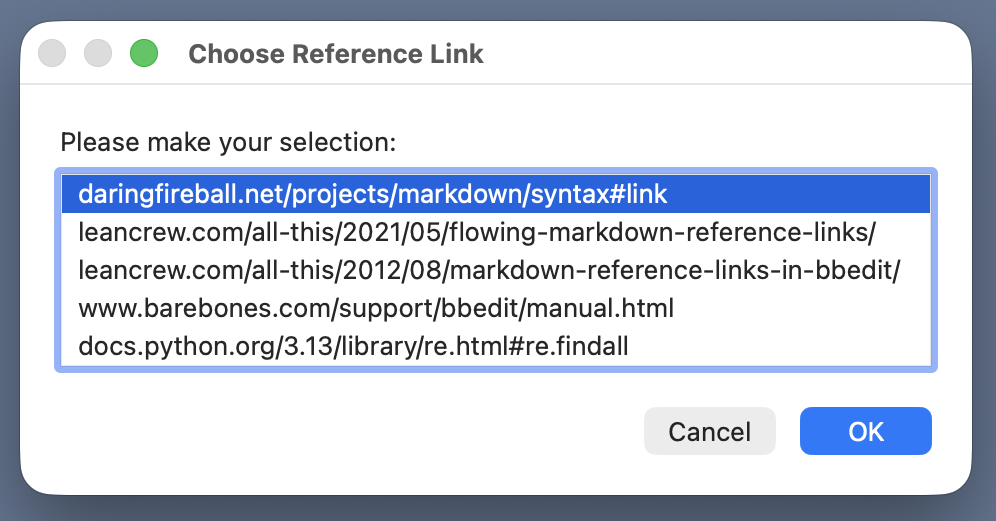
The next section of code, Lines 18–28, builds an AppleScript that makes this “choose from list” prompt. First, it makes a Python list of the third tuple item from each element of refs. Line 19 turns that list into a string, choices, with the format of an AppleScript list. The first item of the list is going to be the default item; its AppleScript string is built in Line 20. Finally, Lines 21–28 assemble the AppleScript that will put up the prompt window and collect the result.
Lines 31–35 run the AppleScript via subprocess.run and osascript. If the user makes a selection, the text of that selection is put into the choice variable. If the user cancels, the script ends with no output.
The last chunk of code, Lines 38–39, uses choice to figure out the reference number of the selection and prints it to standard output.
Before moving on to the AppleScripts that actually insert the reference links, I want to draw your attention to the shebang lines in the two utility scripts. These are exactly what I’d use if I were writing a script meant to be run from the command line. Scripts that aren’t run from the Terminal2 often don’t get the same environment as those that are. But in one of its many thoughtful touches, BBEdit reads your command line environment directly—I guess by looking through your various bash or zsh configuration files—so you don’t have to pull any special tricks to get your scripts to run.
The link-making AppleScripts
BBEdit has a large AppleScript dictionary, and the scripts in this section take advantage of that to move the cursor around—essential when writing reference links—and to behave differently depending on whether text is selected or not. All the scripts are stored in the Blogging subfolder of the Blogging package’s Scripts folder.
Most of the following AppleScripts call—via the do shell script syntax—one of the two Python utility scripts above. You may well ask why I needed two languages to get the work done. Two reasons:
- Regular expressions seemed to be the natural way to find the existing reference links, and AppleScript doesn’t have regular expressions. Now it’s true that Daniel Jalkut made an AppleScript regex dictionary available (for free!) through his FastScripts utility, but that leads to the second reason…
- Which is that when dealing with text and slicing and dicing lists, I feel much more comfortable working in Python than in AppleScript. I’m happy to work in AppleScript for the cursor control, but I would hate using it for the work done in
nextreflinkandgetreflink. Even thoughgetreflinkitself calls out to AppleScript.
Overall, I found the friction that came with using two languages preferable to the friction I’d run into using AppleScript alone.
With that said, let’s explore the AppleScripts themselves.
Clipboard Link
I’m starting with this one because it’s the simplest and probably the most obvious. Lots of people have made AppleScripts, Shortcuts, and Keyboard Maestro macros for making Markdown inline links starting with a URL on the clipboard. This script is one level of complexity up from that.
If text is selected, this turns that text into a reference link to the URL on the clipboard. If no text is selected, it creates an empty reference link where the cursor was. In both cases, the new reference link with an incremented number is put at the bottom of the text and the cursor is moved to a convenient location. Here’s the code:
applescript:
1: -- Get the path to the Resources directory in the package.
2: tell application "Finder"
3: set cPath to container of container of container of (path to me) as text
4: end tell
5: set rPath to (POSIX path of cPath) & "Resources/"
6:
7: set myURL to the clipboard
8:
9: tell application "BBEdit"
10: set oldClipboard to the clipboard
11: set the clipboard to contents of front document as text
12: set myRef to do shell script "pbpaste | " & quoted form of (rPath & "nextreflink")
13: set the clipboard to oldClipboard
14:
15: if length of selection is 0 then
16: -- Add link with empty text and set the cursor between the brackets.
17: set curPt to characterOffset of selection
18: select insertion point before character curPt of front document
19: set selection to "[][" & myRef & "]"
20: select insertion point after character curPt of front document
21:
22: else
23: -- Turn selected text into link and put cursor after the reference.
24: add prefix and suffix of selection prefix "[" suffix "]" & "[" & myRef & "]"
25: select insertion point after last character of selection
26: end if
27:
28: -- Add the reference at the bottom of the document and reset cursor.
29: set savePt to selection
30: select insertion point after last character of front document
31: set selection to "[" & myRef & "]: " & myURL & return
32: select savePt
33: activate
34: end tell
Lines 2–5, which we’ll use in most of the scripts in this section, get the path to the Resources directory by using AppleScript’s clever path to me construction. The unfortunately long container to container to container bit comes from the folder hierarchy shown above. Our AppleScripts are in the Blogging subdirectory of the Scripts directory of the Blogging package, so we have to go up three levels before going down a level into the Resources directory. There’s also a conversion in Line 5 from AppleScript’s native colon-separated path format to Unix’s slash-separated path format.
Line 7 just puts the URL on the clipboard into the variable myURL. This wasn’t necessary, but it creates a parallelism between this AppleScript and the others.
The rest of the script manipulates BBEdit to make a reference link. Lines 10–13 pass the text of the front BBEdit document to the getnextref utility script via the clipboard and the pbpaste command. The reference number returned is stored in the myRef variable. Lines 10 and 13 are a common AppleScript construct used to save and restore the original clipboard contents.
If no text is selected, Lines 17–20 insert an empty set of brackets followed by the bracketed reference number, e.g., [][1], at the cursor. The cursor is then moved between the empty brackets so I can type in the link text.
If text is selected, it’s taken to be the link text. Lines 24–25 surround the selected text with brackets, put the bracketed reference number after it, and put the cursor after the last bracket.
The last step is to add the reference to the bottom of the document. Lines 29–32 save the current cursor position in savePt, jump to the end of the text, insert the reference in the form
[1]: https://myurl.com
and then move back to savePt. Because cursor positions are counted from the beginning of the document, adding text to the end doesn’t change the position savePt refers to.
Safari Front Link
This is the one I use most often. It’s at the top of the Blogging submenu and has been assigned the simplest keyboard shortcut: ⌃L.
It works the same way as Clipboard Link, except it gets the URL from the frontmost Safari tab instead of the clipboard. You might well ask why I bother with Safari Front Link when I have Clipboard Link. I could, after all, select the URL in Safari, put it on the clipboard, and then run Clipboard Link. My answer is that I don’t want to perform those two extra steps when I don’t have to.
Here’s the code:
applescript:
1: -- Get the path to the Resources directory in the package.
2: tell application "Finder"
3: set cPath to container of container of container of (path to me) as text
4: end tell
5: set rPath to (POSIX path of cPath) & "Resources/"
6:
7: tell application "System Events"
8: set pNames to name of every process
9: if "Safari" is in pNames then
10: try
11: tell application "Safari" to set myURL to the URL of the front document
12: on error
13: do shell script "afplay /System/Library/Sounds/Funk.aiff"
14: return
15: end try
16: else
17: do shell script "afplay /System/Library/Sounds/Funk.aiff"
18: return
19: end if
20: end tell
21:
22: tell application "BBEdit"
23: set oldClipboard to the clipboard
24: set the clipboard to contents of front document as text
25: set myRef to do shell script "pbpaste | " & quoted form of (rPath & "nextreflink")
26: set the clipboard to oldClipboard
27:
28: if length of selection is 0 then
29: -- Add link with empty text and set the cursor between the brackets.
30: set curPt to characterOffset of selection
31: select insertion point before character curPt of front document
32: set selection to "[][" & myRef & "]"
33: select insertion point after character curPt of front document
34:
35: else
36: -- Turn selected text into link and put cursor after the reference.
37: add prefix and suffix of selection prefix "[" suffix "]" & "[" & myRef & "]"
38: select insertion point after last character of selection
39: end if
40:
41: -- Add the reference at the bottom of the document and reset cursor.
42: set savePt to selection
43: select insertion point after last character of front document
44: set selection to "[" & myRef & "]: " & myURL & return
45: select savePt
46: activate
47: end tell
The only difference between this and Clipboard Link is Lines 7–28, which get the URL of Safari’s frontmost tab and save it to the variable myURL. Specifically, this is done in Line 11. The rest of this chunk of code is all about error handling. If Safari isn’t running—or if it doesn’t have a window, or if that window’s frontmost tab is empty—the script will play an error sound and stop.
Safari Choose Link
Sticking with the subject of getting links from Safari, let’s consider the situation in which I know I have a Safari tab open to the page I want to link to, but it’s not in the front tab. The Safari Choose Link script presents a list of all the tabs in Safari’s front window for me to choose from (I very rarely have more than one Safari window open). It looks like this:
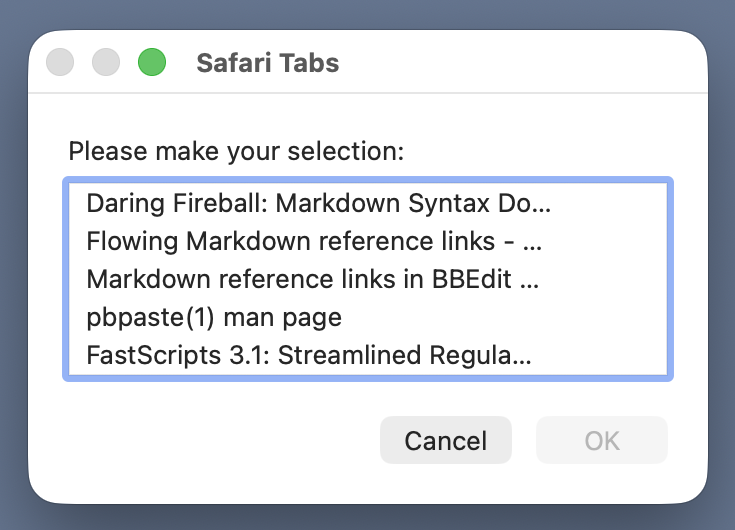
The pages are presented according to their titles. Initially, none of them are selected, but as soon as I select one—which I can do with the up and down cursor keys—the OK button will activate. From this point, the script acts just like Safari Front Window.
Here’s the code:
applescript:
1: -- Get the path to the Resources directory in the package.
2: tell application "Finder"
3: set cPath to container of container of container of (path to me) as text
4: end tell
5: set rPath to (POSIX path of cPath) & "Resources/"
6:
7: on shortened(s)
8: if length of s > 40 then
9: set s to (characters 1 thru 35 of s as text) & "…"
10: end if
11: return s
12: end shortened
13:
14: tell application "System Events"
15: set pNames to name of every process
16: if "Safari" is in pNames then
17: try
18: tell application "Safari"
19: -- Initialize
20: set tabNames to {}
21: set tabURLs to {}
22:
23: -- Collect the tab names and URLs from the top Safari window
24: set topWindow to window 1
25: set topTabs to every tab of topWindow
26: repeat with t in topTabs
27: set end of tabNames to my shortened(name of t)
28: set end of tabURLs to URL of t
29: end repeat
30: end tell
31:
32: -- Display a list of names for the user to choose from
33: activate
34: choose from list tabNames with title "Safari Tabs"
35: set nameChoice to item 1 of result
36: repeat with tabNumber from 1 to the count of tabNames
37: if item tabNumber of tabNames is nameChoice then
38: set myURL to item tabNumber of tabURLs
39: exit repeat
40: end if
41: end repeat
42: on error
43: do shell script "afplay /System/Library/Sounds/Funk.aiff"
44: tell application "BBEdit" to activate
45: return
46: end try
47: else
48: do shell script "afplay /System/Library/Sounds/Funk.aiff"
49: return
50: end if
51: end tell
52:
53: tell application "BBEdit"
54: set oldClipboard to the clipboard
55: set the clipboard to contents of front document as text
56: set myRef to do shell script "pbpaste | " & quoted form of (rPath & "nextreflink")
57: set the clipboard to oldClipboard
58:
59: if length of selection is 0 then
60: -- Add link with empty text and set the cursor between the brackets.
61: set curPt to characterOffset of selection
62: select insertion point before character curPt of front document
63: set selection to "[][" & myRef & "]"
64: select insertion point after character curPt of front document
65:
66: else
67: -- Turn selected text into link and put cursor after the reference.
68: add prefix and suffix of selection prefix "[" suffix "]" & "[" & myRef & "]"
69: select insertion point after last character of selection
70: end if
71:
72: -- Add the reference at the bottom of the document and reset cursor.
73: set savePt to selection
74: select insertion point after last character of front document
75: set selection to "[" & myRef & "]: " & myURL & return
76: select savePt
77: activate
78: end tell
The new parts of this script start with the shortened function on Lines 7–12. It clips the given string; we’ll use this later to keep page titles at a manageable length in the Safari Tabs window.
Lines 18–29 get the titles of the Safari tabs, shorten them if appropriate, and put them in the list form needed by choose from list. In parallel, it makes a list of all the associated URLs. These lists are called tabNames and tabURLs, respectively.
Lines 34–41 then ask the user to choose from the list of titles and figure out the URL that goes with the chosen title. That’s put into the variable myURL.
The rest of Lines 14–51 are error handling, and Lines 53–78 are the same cursor-handling code used in Clipboard Link and Safari Front Link.
All Safari Tab Links
Another Safari script? Yes, but this one is really short.
Sometimes I know that every tab in Safari is going to be linked to in the post I’m writing. In that situation, why not just add links to all the tabs to the bottom of the document right now? I’ll then make links to them in the body of the text using the Old Link script, which we’ll cover next.
Here’s the AppleScript for All Safari Tab Links:
applescript:
1: set n to 1
2: set refs to ""
3: tell application "Safari"
4: repeat with thisTab in (every tab of front window)
5: set refs to refs & "[" & n & "]: " & (URL of thisTab) & linefeed
6: set n to n + 1
7: end repeat
8: end tell
9:
10: tell application "BBEdit"
11: set savePoint to selection
12: select insertion point after last character of front document
13: set selection to refs
14: select savePoint
15: end tell
I told you it was going to be short. Lines 1–8 build the reference link text one line at a time by looping through the tabs. When the loop is done, the variable refs contains text like this:
[1]: https://daringfireball.net/projects/markdown/syntax#link
[2]: https://leancrew.com/all-this/2021/05/flowing-markdown-reference-links/
[3]: https://leancrew.com/all-this/2012/08/markdown-reference-links-in-bbedit/
[4]: https://leancrew.com/all-this/man/man1/pbpaste.html
[5]: https://redsweater.com/blog/3822/fastscripts-3-1-streamlined-regular-expressions
Lines 10–15 then save the cursor location, jump to the bottom of the document, insert refs, and jump back to the saved location. That’s it. Because this script is intended to be run before I start writing, it can start the reference numbering at 1, and there’s no need to call nextreflink.
Old Link
Finally, here’s the script I run when a link is already in the list at the bottom of the file. Now, there’s nothing wrong with repeating links. Having, for example, a list like this at the bottom of a Markdown file,
[1]: https://daringfireball.net/projects/markdown/syntax#link
[2]: https://leancrew.com/all-this/2021/05/flowing-markdown-reference-links/
[3]: https://daringfireball.net/projects/markdown/syntax#link
[4]: https://leancrew.com/all-this/2012/08/markdown-reference-links-in-bbedit/
[5]: https://leancrew.com/all-this/man/man1/pbpaste.html
[6]: https://daringfireball.net/projects/markdown/syntax#link
[7]: https://redsweater.com/blog/3822/fastscripts-3-1-streamlined-regular-expressions
with the Daring Fireball URL associated with a handful of reference numbers, will produce the same HTML as a list of unique URLs. But I can’t imagine anyone wanting a list like that. To me, the Markdown should look as nice as the resulting HTML. If I have several links to the same URL, they should have the same reference number in the body of the text. Hence the Old Link script.
applescript:
1: -- Get the path to the Resources directory in the package.
2: tell application "Finder"
3: set cPath to container of container of container of (path to me) as text
4: end tell
5: set rPath to (POSIX path of cPath) & "Resources/"
6:
7: tell application "BBEdit"
8: set oldClipboard to the clipboard
9: set the clipboard to contents of front document as text
10: set myRef to do shell script "pbpaste | " & quoted form of (rPath & "getreflink")
11: set the clipboard to oldClipboard
12:
13: if myRef is not "" then
14: if length of selection is 0 then
15: -- Add link with empty text and set the cursor between the brackets.
16: set curPt to characterOffset of selection
17: select insertion point before character curPt of front document
18: set selection to "[][" & myRef & "]"
19: select insertion point after character curPt of front document
20:
21: else
22: -- Turn selected text into link and put cursor after the reference.
23: add prefix and suffix of selection prefix "[" suffix "]" & "[" & myRef & "]"
24: select insertion point after last character of selection
25: end if
26: end if
27: activate
28:
29: end tell
Lines 2–5 are the same as most of the other scripts. Lines 8–11 are similar to the other scripts, but Line 10 calls getreflink instead of nextreflink. That lets me choose the value of myRef from the list of URLs already being used. The remainder of the script is the same as Clipboard Link, Safari Front Link, and Safari Choose Link.
Final thoughts
I’m not providing a download link to my Blogging package. It contains a lot of other stuff that’s specific to ANIAT and my publishing system. And if you’re really interested in using any of these scripts, a little copying and pasting won’t do you any harm.
Normally, BBEdit puts the scripts in alphabetical order in the menu, but you can get around that by prefixing the name of your script with a number followed by a closing parenthesis. BBEdit will then arrange the menu in numerical order according to the prefixes but won’t include the prefixes in the menu items. So my Scripts folder in the Blogging package has files with the names
00)Safari Front Link.scpt
01)Old Link.scpt
02)Clipboard Link.scpt
04)Safari Choose Link.scpt
05)All Safari Tab Links.scpt
among others.
The order of the scripts in the menu reflects my sense of how often I use them, even though All Safari Tab Links is the only one I call from the menu instead of via a keyboard shortcut. It’s by far the least used, and there’s no need for a quick way to run it. All the keyboard shortcuts use ⌃L; the added modifier keys were chosen either at random or through a process I have no memory of.
Proofreading with ChatGPT
October 12, 2025 at 11:21 AM by Dr. Drang
I was talking with David Sparks and Stephen Hackett recently, and the conversation came around to fixing typos and other errors in our writing. I think the typos and poorly constructed sentences here at ANIAT have been reduced since I started having my Mac read my posts aloud to me.
I do this by converting the Markdown source of a post into HTML and previewing it in Safari. Then I go through the post, selecting one paragraph at a time and typing ⌥⎋ (that’s Option-Escape) to speak the selected text. This works because I have the option turned on in the section of the Accessibility settings. You might want to read Apple’s instructions for this.
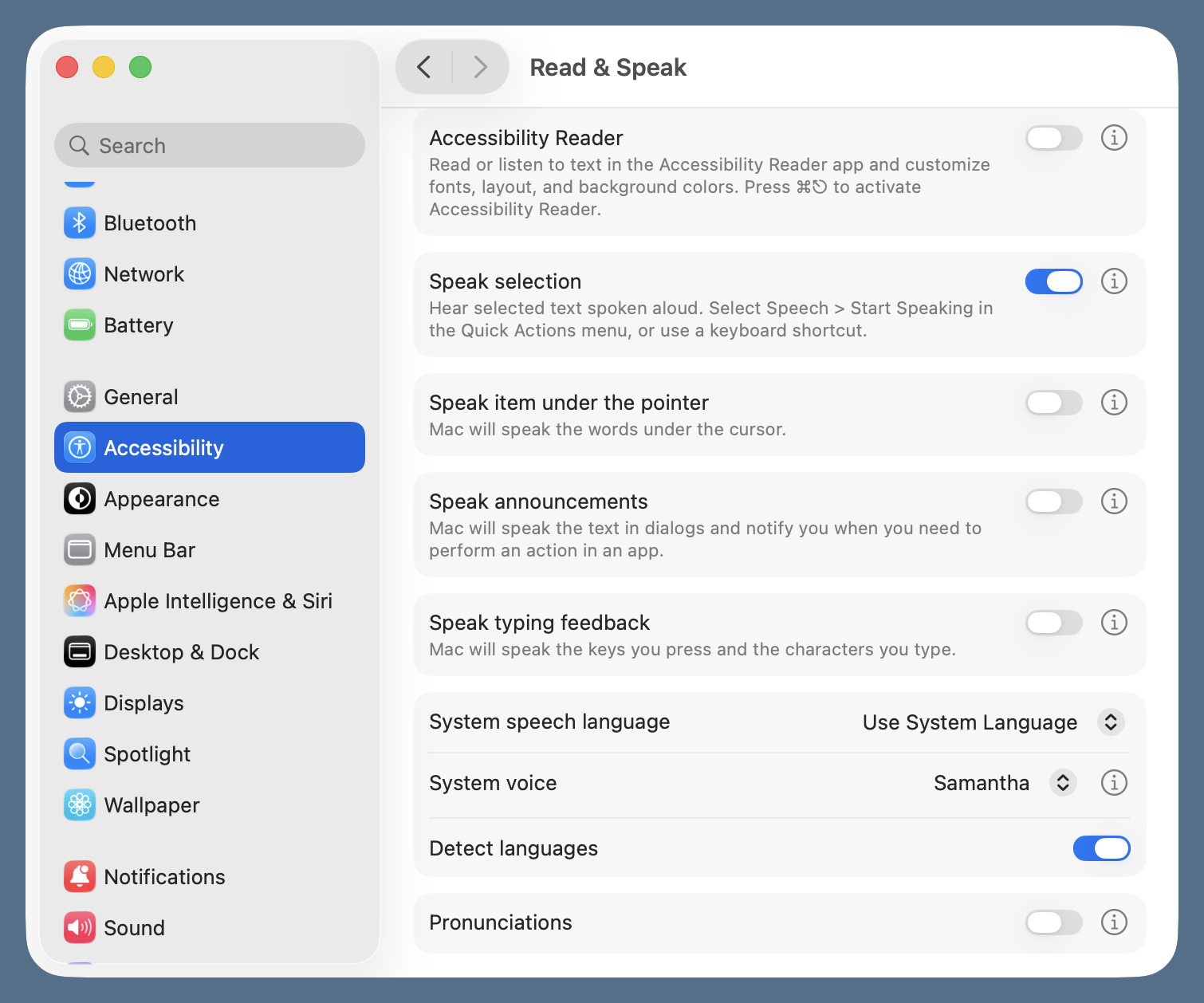
It’s embarrassing how many mistakes I find this way, but what’s more embarrassing is that mistakes still squeak through. David suggested having an LLM read my posts and tell me where it thinks the mistakes are. Make sure, he emphasized, to tell it to just find and report the mistakes—don’t fix them. And because many of my posts contain programs, I should also tell it to ignore sections of code.
So I did just that, albeit for a post I’d already published, and I thought it worthwhile to go through the results.
I meant to use both ChatGPT and Claude, but I messed up and sent a different (partially corrected) version of the text to Claude, so I’m going to ignore its results.
Here’s the prompt I gave to ChatGPT:
Find typographical errors and grammatical mistakes in the following Markdown text. Do not make any changes, just tell me what you think should be changed. Ignore all embedded URLs and programming code.
The text I gave it was the Markdown source of my most recent post, the one about scoring my incorrect basketball trivia answers by calculating things like its Levenshtein distance from the correct answer. What follows is ChatGPT’s analysis of the text and my comments.
Inline code discrepancy:
You mention the wrong answer asADCBbut later say “you can’t go from ACDB to BDCA.” That looks like a typo (ACDB instead of ADCB).
This is the best of ChatGPT’s findings. In a post that includes a discussion of letter transposition errors, having (non-deliberate) letter transposition errors is a big mistake. After reading this, I searched for ACDB, ADCB, BDCA, and BCDA to find this sort of mistake and make sure my right and wrong answers were always right.
Ellipsis usage:
In “There are words that don’t follow the ‘I before E’ rule—Levenshtein, to pick a random example—”, the em dashes are fine stylistically, but for Markdown consistency you could ensure they are either — or — consistently.
This is inexplicable for a couple of reasons:
- It has nothing to do with ellipses.
- I was consistent in my use of em dashes throughout the post.
To make sure there were no en dashes or hyphens where em dashes should be, I searched the document for them. There were no en dashes whatsoever, and all the hyphens were in either URLs or hyphenated words (like Damerau-Levenshtein).
Although Markdown allows you to use double hyphens to indicate an em dash—following the typewriter tradition I learned over 50 years ago—it doesn’t require you to. I learned how to get en and em dashes via ⌥- and ⇧⌥- from The Mac is Not a Typewriter and have been using those keystrokes ever since.
Misused plural agreement:
“two switches, Majerle/Nash and Chambers/Hawkins would’ve made my answer correct.” → Should be “would have made” (avoid contraction in formal writing).
Again, the heading for this mistake doesn’t seem to match the description. Maybe the subject of the post made ChatGPT think1 this was formal writing. Next time, I’ll point out that this is a blog post and is meant to have a conversational tone.
Comma after introductory clause (minor stylistic):
“Anyway, I got every number wrong, but I noticed that two switches…” → Grammatically fine, though “Anyway” is informal — could be replaced with “In any case,” if desired.
Again, it seems to think this is more formal writing than it is. Also, I believe an introductory “Anyway,” like most introductory words and phrases, should be followed by a comma.
Missing comma before a nonrestrictive clause:
“The Damerau-Levenshtein distance from my answer to the correct one is 3; substitution of the first character, substitution of the last character, and transposition of the two interior characters.” → Could use a colon instead of semicolon before the list: “…is 3: substitution of…”
The description of the typo is correct. I did intend for that to be a colon; my left pinky lifted off the Shift key before my right pinky did its job. But the heading is wrong.
Incorrect use of “Levenshtein calculation” example:
“Since switching letters isn’t a valid edit in a Levenshtein calculation, you can’t go from ACDB to BDCA…” → Again, that appears to be a typo — the example string ACDB should match your earlier ADCB.
This is another transposition error. Here, though, I got the interior letters backwards in both strings—it should be ADCB and BCDA—and ChatGPT found only one of the mistakes.
Missing article:
“We’ve reduced both of these edit distances without really changing the question.” → Could be “…without really changing the nature of the question.” (Optional clarity fix.)
There’s no missing article, so we have another incorrect heading, and I think inserting “the nature” is redundant. To me, my use of “really” indicates that I’m not changing the nature of the question.
Awkward phrase:
“There are a few ways to import functions for Python.” → More idiomatic: “There are a few ways to use these functions in Python” or “to import such functions in Python.”
It wasn’t awkward, it was nonspecific. I meant to say “There are a few ways to import similar functions for Python” and have since added the missing word.
I’m glad ChatGPT pointed me to this sentence, even though it mischaracterized my mistake and gave corrections I didn’t like.
Incorrect pluralization / parallelism:
“Mathematica has the built-in functions [HammingDistance], [EditDistance], and [DamerauLevenshteinDistance]. There are a few ways to import functions for Python.” → Grammatically fine, but the flow is a little inconsistent (switches from “has built-in functions” to “ways to import functions”).
This is the same sentence flagged above. While I appreciate the desire for parallel construction, I can’t use it here. Unlike Mathematica, Python itself doesn’t have built-in edit distance functions—they have to be imported.
Comma splice or fragment:
“Since my answer can be made correct by flipping two pairs of letters, I wondered which of the other derangements can be similarly transformed.” → Fine grammatically, but stylistically “could be similarly transformed” would match past-tense context.
This is not a comma splice, so the header is wrong again. And I don’t see this as having inconsistent tense. To me, “can be made” is not past tense.
Ambiguous reference:
“Because I didn’t try to be clever in setting up the nested loops, the count variable is incremented twice for every pair of characters that can be flipped.” → Grammatically fine, but the pronoun “that” could be “which” for restrictive vs. nonrestrictive correctness.
Flatly wrong. “Can be flipped” absolutely restricts the character pairs being discussed.
Unnecessary comma in bullet:
“CDAB and ABCD, which are one-character rotations…” → The comma after ABCD is optional; can be removed for cleaner reading.
No, the commas are necessary.
Incorrect number in final sentence:
“There’d be 44 derangements in a 5-player question.” → The actual number of derangements for 5 items is 44, so it’s mathematically correct — not an error, just worth double-checking the intent (it matches your topic).
The sentence before the flagged one is: “I’m glad this question had only four players.” Maybe that confused ChatGPT into thinking I meant to get the number of derangements of four items instead of five. Anyway, there are no incorrect numbers in the final sentence.
Stylistic repetition:
The phrase “the correct answer” appears very frequently; while not grammatically incorrect, it may benefit from varied phrasing for readability.
There are two reasons I tend to avoid the varied phrasing ChatGPT wants:
- In my reports for work, using different words for the same thing often led to questions. “You say ‘correct answer’ here but ‘right answer’ over here. Why did you make that distinction?” Consistent phrasing avoided stupid questions like that, and I’ve carried the habit over to my writing here.
- English isn’t the first language of many of my readers. I think sticking with the same words for the same thing is helpful for them.
So was this a success? Yes and no. I definitely found mistakes I didn’t find by listening to the post read aloud, but I also wasted some time looking into “mistakes” that weren’t. And even when ChatGPT pointed me to a sentence with an error, the error wasn’t always what ChatGPT said it was.
Overall, though, the post was improved, so I’m going to give it another try. And I’ll still have my Mac read the text back to me. In addition to finding errors, I often think of different ways to explain things while listening.
-
There are people—Emily Bender being perhaps the most prominent—who get very upset with this language. “LLMs don’t think!” they complain. True enough, but as someone who has spent decades talking about how beams “want” to deflect in a certain way, I find this kind of anthropomorphism harmless. It also makes sentences about LLMs much easier to write. I suppose there is a danger that some will take the word “think” literally, but I have a higher opinion of my readers. ↩
Basketball trivia, editing distances, and derangement
October 8, 2025 at 2:40 PM by Dr. Drang
My older son and I have been playing a daily basketball trivia game. Here’s the question from yesterday with my answers handwritten on the sheet.

Here’s the text of the question. This is easier than trying to put it in the image’s alt text.
Match the Suns great with his retired uniform number.
1. Tom Chambers A. 42 2. Steve Nash B. 24 3. Dan Majerle C. 13 4. Connie Hawkins D. 9
The correct answer, in player order, is BCDA, not my answer of ADCB. I won’t blame anyone who scoffs at my failure to get Nash’s number right. My excuse is that I thought it was so obvious for a smart playmaking guard to wear #13 that it had to be wrong. So I chose Majerle for #13 instead. This sort of mistake is often called “outsmarting” oneself, but I think it’s more “outstupiding.”
Anyway, I got every number wrong, but I noticed that two switches, Majerle/Nash and Chambers/Hawkins, would’ve made my answer correct. I knew there were various methods for measuring edit distances of text strings and wondered if any of them would provide guidance on how “close” my answer was.
The simplest is the Hamming distance, which is just a count of how many characters are wrong. It’s limited to comparing strings of equal length, which is fine for this situation. Since every character in my answer is wrong, its Hamming distance from the correct answer is 4.
I’ve seen lots of references to the Levenshtein distance but have never used it or read up on it before now. It’s a count of the number of single-character insertions, deletions, and substitutions necessary to go from one string to another. The Levenshtein distance from my answer to the correct one is also 4. Since switching letters isn’t a valid edit in a Levenshtein calculation, you can’t go from ADCB to BCDA in fewer steps than 4 substitutions.
There’s also a Damerau-Levenshtein distance, which extends the Levenshtein idea by allowing the transposition of adjacent characters as one of the editing steps. The Damerau-Levenshtein distance from my answer to the correct one is 3: substitution of the first character, substitution of the last character, and transposition of the two interior characters.
After doing these calculations, I started thinking about how these last two distances are better for evaluating actual words than strings like the trivia answer. For example, in the Damerau-Levenshtein calculation, we’re allowed to switch only adjacent characters, not characters that are two or more positions apart. This makes sense when dealing with words. We’ve all typed teh or hte, and some of us have text substitutions set up to transform them automatically into the. Also, there are words that don’t follow the “I before E” rule—Levenshtein, to pick a random example—which makes them easy to misspell by switching adjacent letters.
But the answer to this trivia question isn’t like a word. The question would be effectively the same if it were worded this way:
Match the Suns great with his retired uniform number.
1. Connie Hawkins A. 42 2. Tom Chambers B. 24 3. Steve Nash C. 13 4. Dan Majerle D. 9
I’ve kept the uniform numbers in the same order but rotated Connie Hawkins up to the top of the list. This is the same question as before, but now the correct answer is ABCD and my incorrect answer would be BADC. The Damerau-Levenshtein distance between these strings is just 2: transpose the first two characters, then the last two characters. Also, the Levenshtein distance would be 3:
BADC→ADC→ABC→ABCD
We’ve reduced both of these edit distances without really changing the question. So these measures aren’t a good way to see how bad my answer was.
Both Mathematica and Python have functions for calculating these distances. Mathematica has the built-in functions HammingDistance, EditDistance (for Levenshtein), and DamerauLevenshteinDistance. There are a few ways to import similar functions for Python. I used the textdistance module, but jellyfish is apparently quite a bit faster.
There are 24 (4!) different ways to answer the trivia question:
ABCD BACD CABD DABC
ABDC BADC CADB DACB
ACBD BCAD CBAD DBAC
ACDB BCDA CBDA DBCA
ADBC BDAC CDAB DCAB
ADCB BDCA CDBA DCBA
These are the permutations of the correct answer BCDA.1 Of these, 9 get every player wrong:
CBAD DBAC ABCD
CDAB DABC ADBC
CABD DACB ADCB
My wrong answer is the one in the lower left corner. These are known as the derangements of the correct answer, so called because they’re the permutations of BCDA with none of the letters in their original (correct) position. I wrote a post on calculating the number of derangements back in 2020.
Since my answer can be made correct by flipping two pairs of letters, I wondered which of the other derangements can be similarly transformed. It’s not hard to go through the 9 strings above and work it out by hand, but I wanted to write a little script to do it. Here it is:
python:
1: #!/usr/bin/env python3
2:
3: from itertools import permutations
4:
5: def hasmatches(s1, s2):
6: return sum(x == y for x, y in zip(s1, s2)) > 0
7:
8: def twoflips(s1, s2):
9: if hasmatches(s1, s2):
10: return False
11: else:
12: count = 0
13: for i1, c1 in enumerate(s1):
14: for i2, c2 in enumerate(s2):
15: if c1 == c2 and s1[i2] == s2[i1]:
16: count += 1
17: return count == 4
18:
19: correct = 'BCDA'
20: perms = [ ''.join(x) for x in permutations(correct) ]
21: allbad = [ x for x in perms if not hasmatches(correct, x) ]
22: flippers = [ x for x in allbad if twoflips(x, correct) ]
23:
24: print(flippers)
The hasmatches function uses a generator to loop through a pair of strings, summing up how many of their characters match by position. If the sum is greater than zero, it returns True.
The twoflips function is more complicated, but it does a similar thing. It loops through both strings and checks whether the ith character of one string matches the jth character of the other and vice versa. As it proceeds, it counts all of these occurrences. Because I didn’t try to be clever in setting up the nested loops, the count variable is incremented twice for every pair of characters that can be flipped. That’s why twoflips returns True when count equals 4.
The rest of the program is more obvious. perms gets the list of all 24 permutations; allbad filters them down to just the 9 that have no matches; and finally, flippers filters allbad down to the 3 permutations that can be turned into the correct answer by performing two letter exchanges. The result is
CBAD DABC ADCB
which includes my answer.
Looking through the remaining derangements, we see
CDABandABCD, which are one-character rotations of the correct answer; andDBAC,ADBC, andCABD, whose connection to the correct answer isn’t clear to me.
I’m glad this question had only four players. There’d be 44 derangements in a 5-player question.
-
Or of
ABCD. OrADCB. Permutations cover all the ways of arranging the four characters. I think it’s easiest to understand the arrangements when they’re laid out like this. ↩
