And now it’s all this

I just said what I said and it was wrong
Or was taken wrong

Square roots and maxima

November 29, 2024 at 7:11 PM by Dr. Drang

A few days ago, I saw this short YouTube video from Grant Sanderson at 3Blue1Brown:

The gist of the video is that if you have three independent random variables, $X_1$, $X_2$, and $X_3$, that are all uniformly distributed between 0 and 1, then

$$\mathrm{P}[\max (X_1,X_2)\le x]=\mathrm{P}[\sqrt{X_3}\le x]=x^2$$

where $\mathrm{P}[\cdot ]$ represents the probability of the thing in the brackets.

I should mention here that I’m not using the same notation as Grant. The textbook used in the class where I learned this sort of stuff was Ang and Tang’s Probability Concepts in Engineering Planning and Design. They used capital letters for random variables and lowercase letters for particular values. It’s a nice convention that makes it easy to distinguish the random from the nonrandom. I’ve stuck with it for 45 years and don’t intend to change.

The probability $P[X\le x]$ is a function of $x$ and is known as the cumulative distribution function¹ (CDF) of $X$. Therefore, the probabilities given above are the CDFs of the functions $\max (X_1,X_2)$ and $\sqrt{X_3}$.

Grant does his usual excellent job of explaining why these two functions have the same CDF, but if you have any doubts, it’s fairly easy to check his work numerically. This is one of the great advantages of having so much computing power at our disposal.

We’ll generate three sets of $n$ random numbers from the uniform distribution, apply the max and sqrt functions to them, and sort the results in ascending order. Then we can estimate the probabilities by dividing the rank of each value—that is, its position in the sorted list—by $n$.

Let’s look at an example of how this works. We’ll generate 20 random numbers from a uniform distribution between 0 and 1, take their square roots, and sort them. Here are the sorted values, their ranks, and the ranks divided by 20.

Value	Rank	Rank/20
0.15153773	1	0.05
0.31017013	2	0.10
0.32107819	3	0.15
0.36746846	4	0.20
0.47920455	5	0.25
0.51328779	6	0.30
0.55133211	7	0.35
0.65800726	8	0.40
0.72510687	9	0.45
0.76085816	10	0.50
0.80286435	11	0.55
0.81393308	12	0.60
0.82690246	13	0.65
0.90907066	14	0.70
0.91344562	15	0.75
0.91666637	16	0.80
0.91701938	17	0.85
0.94649904	18	0.90
0.94874985	19	0.95
0.99254165	20	1.00

Plotting these points, we get

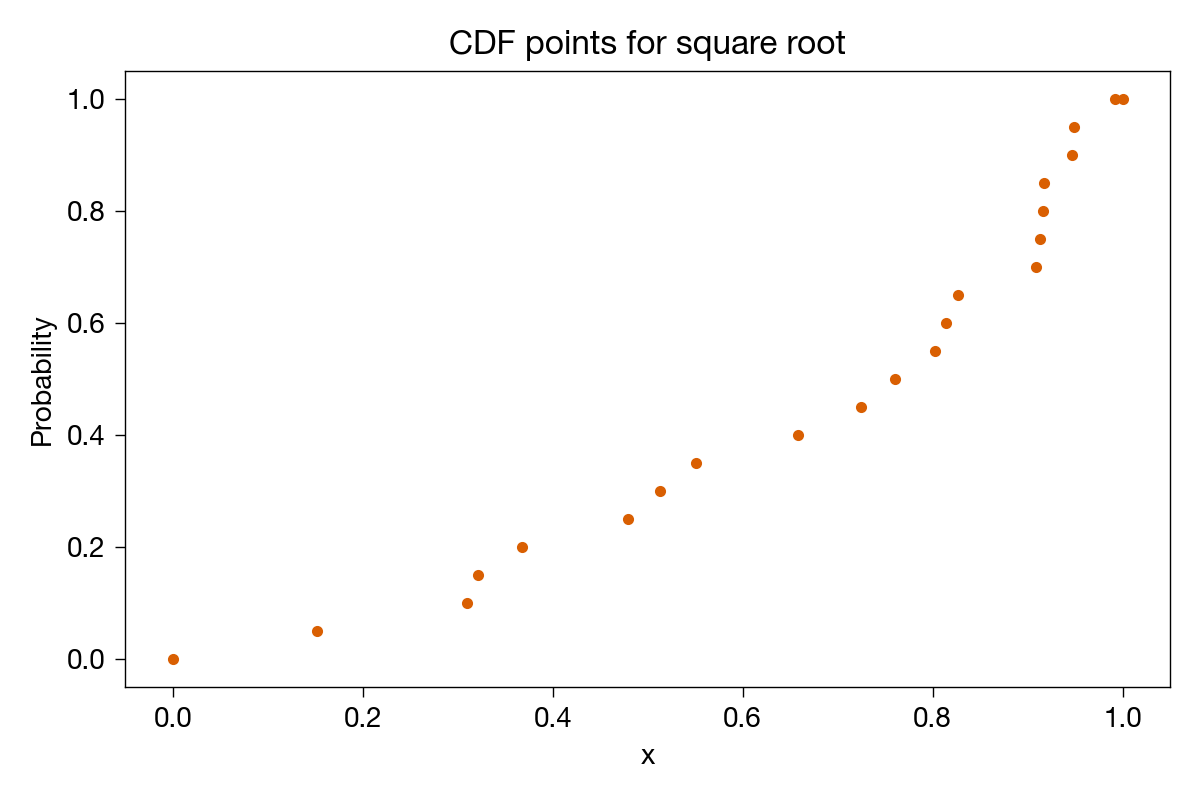
where I’ve added extra points at (0, 0) and (1, 1) to remind us that those are the limits; no value can be less than or equal to 0 and all values must be less than or equal to 1.

To complete the plot, there should be a horizontal line from each point to the next x value, where the function should then jump up to the next point.

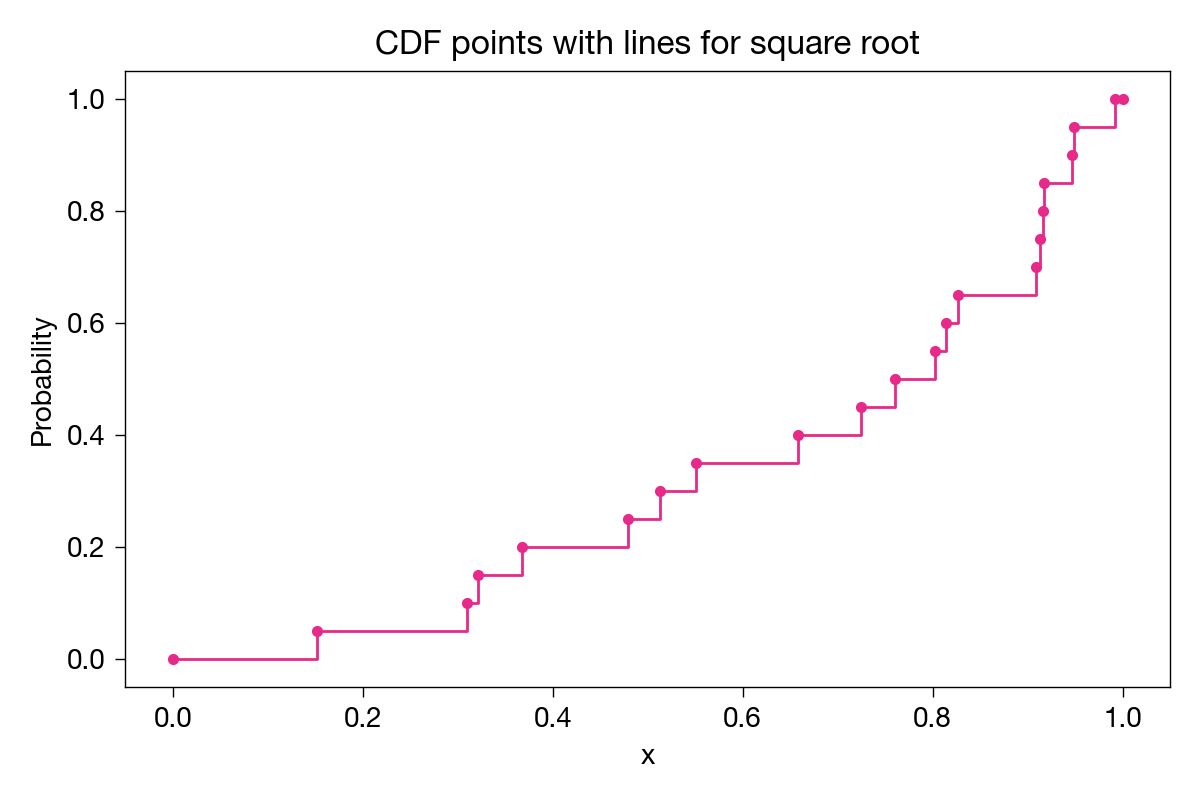
Why? Because, for example, 40% (8 of 20) of the sample values are less than or equal to any value from 0.65800726 (inclusive) and 0.72510687 (exclusive). Similarly for all the other in-between portions of the graph.

Since there’s a step at each x value, we don’t need to show the points, just the lines. Here’s a plot of both the max and sqrt sample CDFs for 20 samples, along with the analytical solution given by Grant:

The sample CDFs look reasonably close to the analytical one. Let’s bump up the number of samples to 100 and see what we get:

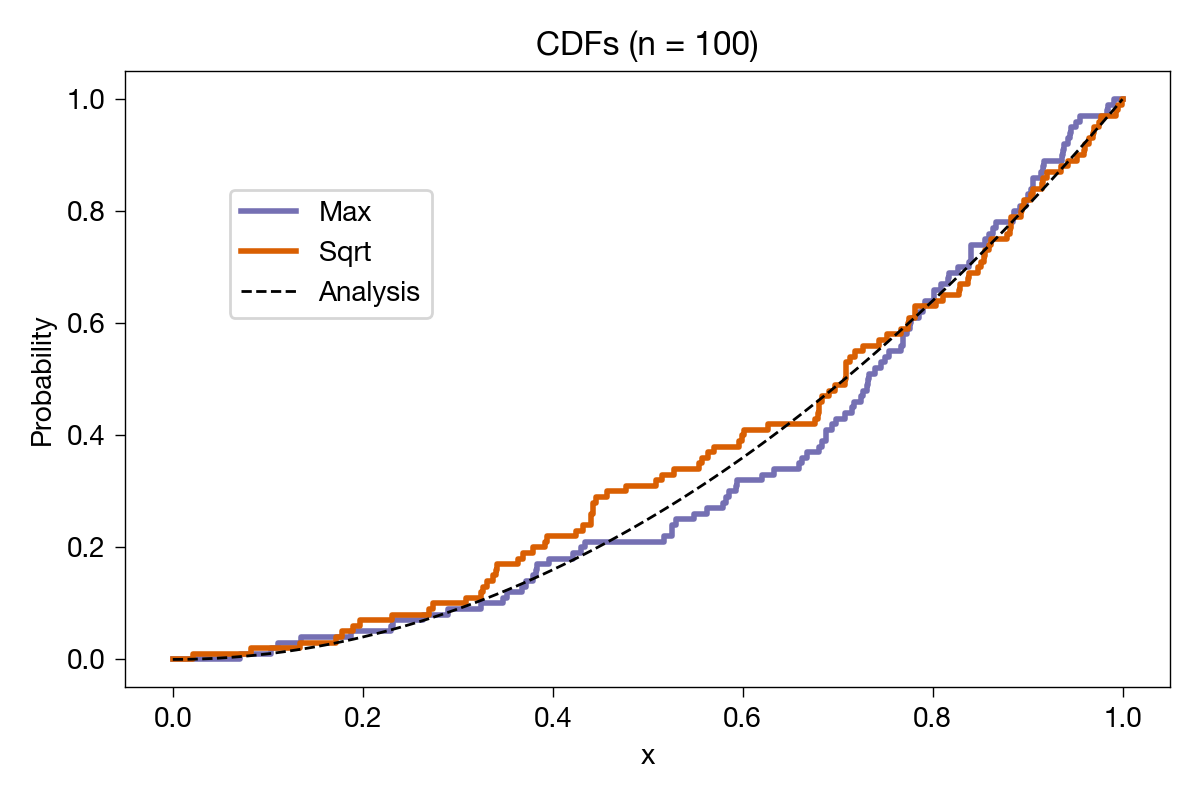
Closer to the analytical result, as expected. Just to be ridiculous, we’ll do it again with 10,000 samples:

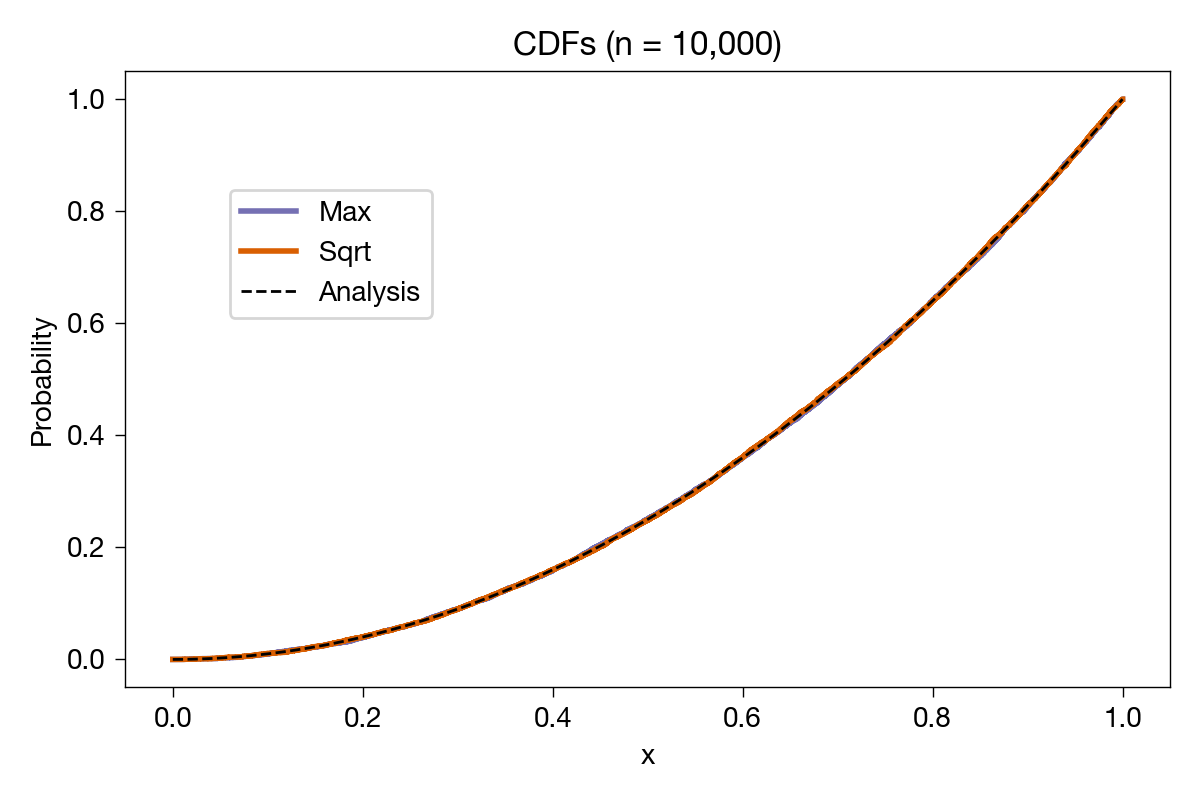
With this many samples, you can’t even see the steps, but it’s clear that both of the sample CDFs are converging to the analytical one.

If you have some background in statistics, you might be expecting me to run the Kolmogorov-Smirnov test to check the goodness of fit between the sample and the analytical CDFs. But I think what we’ve done is a sufficient check on Grant’s work (as if that were needed). You can go ahead with the K-S test on your own.

Although running a numerical check was nice, my main purpose in making these graphs was to see how to use the step method in Matplotlib. It’s a plotting routine made especially for this type of graph. While you can use the usual plot for a stepwise function, you’d have to first construct arrays with two values for every step. The advantage in using step is that it takes care of all that bookkeeping. The arrays you pass to it need only one value for each step; it takes care of plotting the second value automatically.

Here’s the code that produces the graph for 20 samples:

python:
 1:  #!/usr/bin/env python3
 2:  
 3:  import numpy as np
 4:  import matplotlib.pyplot as plt
 5:  
 6:  # CDF by analysis
 7:  x = np.linspace(0, 1, 101)
 8:  cdfAnalysis = x**2
 9:  
10:  # Sample CDFs using random numbers
11:  rng = np.random.default_rng(seed=1732895964)
12:  n = 20
13:  heights = np.linspace(0, n, n+1)/n
14:  heights = np.concatenate((heights, np.ones(1)))
15:  
16:  # Max of two uniform variates
17:  X1 = rng.uniform(0, 1, n)
18:  X2 = rng.uniform(0, 1, n)
19:  Xmax = np.sort(np.maximum(X1, X2))
20:  Xmax = np.concatenate((np.zeros(1), Xmax, np.ones(1)))
21:  
22:  # Sqrt of uniform variate
23:  X3 = rng.uniform(0, 1, n)
24:  Xsqrt = np.sort(np.sqrt(X3))
25:  Xsqrt = np.concatenate((np.zeros(1), Xsqrt, np.ones(1)))
26:  
27:  # Create the plot with a given size in inches
28:  fig, ax = plt.subplots(figsize=(6, 4), layout='tight')
29:  
30:  # Add plots
31:  ax.step(Xmax, heights, where='post', color='#7570b3', lw=2, label='Max')
32:  ax.step(Xsqrt, heights, where='post', color='#e7298a', lw=2, label='Sqrt')
33:  ax.plot(x, cdfAnalysis, '--', color='black', lw=1, label='Analysis')
34:  
35:  # Title and axis labels
36:  plt.title(f'CDFs (n = {n:,d})')
37:  plt.xlabel('x')
38:  plt.ylabel('Probability')
39:  
40:  # Make the border and tick marks 0.5 points wide
41:  [ i.set_linewidth(0.5) for i in ax.spines.values() ]
42:  ax.tick_params(which='both', width=.5)
43:  
44:  # Add the legend
45:  ax.legend(loc=(.1, .6))
46:  
47:  # Save as PDF
48:  plt.savefig(f'20241129-CDF comparison with {n} samples.png', format='png', dpi=200)

The values used to plot the analytical results are given in Lines 7–8. I like NumPy’s linspace function because it works by default the way I think: you give it the start and end values and the number of values to generate and off it goes. No worries about whether the end value is included or not. It is.

The next section, Lines 11–14, sets up the random number generator and the step heights for both the max and sqrt samples. You can specify the seed value for NumPy’s random number generator, which is helpful when you’re editing and debugging code and want to get the same set of values every time you run the script. The seed I used was the time I started writing this code in epoch seconds. I got it from the command line using

date +'%s'

Another advantage of setting the seed is that anyone else who runs the code will get the same plot I got.

Although this code is for 20 samples, Line 12 can be edited to handle any number of samples.

The concatenate function in Line 14 adds an extra 1 to the end of the heights variable. I discussed the reason for doing that earlier in the post. It’s of some small value with just 20 samples but not very useful when we get up to 10,000.

Lines 17–20 generate the x values for the max samples. They generate two sets of random numbers that are uniformly distributed between 0 and 1, get the maximum of each pair, and sort them in ascending order. The concatenate function was then used to add a 0 at the front of the Xmax array and a 1 at the end.

Lines 23–25 generate the x values for the sqrt samples. The process is similar to the max samples but we need to generate only one set of random numbers.

From this point on, it’s all plotting. The key feature is the use of step in Lines 31 and 32. The x values (either Xmax or Xsqrt) and heights are passed to step, and it handles all the plotting. An interesting parameter is where, which can be assigned either pre (the default) or post. The where parameter dictates whether the horizontal parts of the graph are plotted before or after each given point. Because of the way I set up the various arrays, post was the correct choice.

I got the color values in Lines 31 and 32 from the ColorBrewer site. They’re meant to be easy to distinguish for both colorblind and non-colorblind viewers. I suspect there’s a way to specify the ColorBrewer colors in Matplotlib automatically, but I haven’t looked into it.

The only other interesting part of the code is that Lines 36 and 48 change the title and filename according to the number of samples specified on Line 12.

As I said, it’s nice to have computers around to check on your analysis. Numerical integration and differentiation, Monte Carlo simulation, and graphing results are all things that can get you results quickly if you teach yourself how to use the software that’s available. These are certainly not proofs, and there’s always the danger of setting up your computer solution incorrectly—it’s easy to follow the same wrong path numerically that you followed analytically. But when done with care, these checks can give you confidence that you may not have with an analytical solution by itself.

---

The tetrahedral days of Christmas

November 25, 2024 at 11:13 AM by Dr. Drang

I’m pretty sure there’s a Peanuts comic strip in which Linus works out how many of each gift was given in the “Twelve Days of Christmas.” I’ve been unable to Google it, because the search results are overwhelmed by links to “A Charlie Brown Christmas.” So I decided to work it out myself.

It’s obvious that there are 12 partridges in a pear tree, one for each of the 12 days. And it follows that there are 22 turtle doves, two for each of the 11 days after the first. By induction, we can say that the total number of the k^th gift is

$$k(13-k)$$

Here’s a table of the results:

Gift no.	Gift	Total
1	Partridge in a pear tree	12
2	Turtle doves	22
3	French hens	30
4	Calling birds	36
5	Gold rings	40
6	Geese a-laying	42
7	Swans a-swimming	42
8	Maids a-milking	40
9	Ladies dancing	36
10	Lords a-leaping	30
11	Pipers piping	22
12	Drummers drumming	12

Adding up twelve numbers is easy, especially since the symmetry lets you add just the first six and double it. But let’s work out a formula. We start with

$$\underset{k=1}{\overset{12}{\∑}}k(13-k)$$

which we can break into two parts:

$$\underset{k=1}{\overset{12}{\∑}}13k-\underset{k=1}{\overset{12}{\∑}}{k}^2$$

or

$$13\underset{k=1}{\overset{12}{\∑}}k-\underset{k=1}{\overset{12}{\∑}}{k}^2$$

The first of these sums is our friend the triangular number,

$$\underset{k=1}{\overset{n}{\∑}}k=\frac{n(n+1)}{2}$$

which we saw in the post on houses of cards. For $n=12$, the triangular number is

$$\frac{12\cdot 13}{2}=78$$

The second sum comes from a 3D analog to the triangular numbers, the square pyramidal numbers,

$$\underset{k=1}{\overset{n}{\∑}}{k}^2=\frac{n(n+1)(2n+1)}{6}$$

The name comes from building a pyramid of balls with a square base. The top row has just one ball; the row under it has four; the row under that has nine, and so on. The k^th pyramidal number is the total number of balls in a pyramid with n rows. For $n=12$, the square pyramidal number is

$$\frac{12\cdot 13\cdot 25}{6}=650$$

So our total gift count is

$$13\cdot 78-650=1014-650=364$$

which is coincidentally close to the number of days in a year.

We could have kept the formulas algebraic and worked out a single simple formula for the total number of gifts:

$$\underset{k=1}{\overset{n}{\∑}}k(n+1-k)=\frac{n(n+1)(n+2)}{6}$$

This turns out to be a tetrahedral number. Tetrahedral numbers are also called triangular pyramidal numbers; they’re similar to the square pyramidal number but with a triangular base instead of a square.

After working it out, this answer seems obvious in retrospect. It comes from adding the gifts day-by-day instead of gift-by-gift. On the first day, there’s one gift (a partridge); on the second day, there are three gifts (two calling birds and a partridge); on the third day, there are six gifts (three French hens, two calling birds, and a partridge). Each day, you add the next triangular number, which is exactly how the tetrahedral numbers are constructed.

After doing this, I looked up tetrahedral numbers in the Online Encyclopedia of Integer Sequences. It’s sequence A000292, and one of the examples given in the comments is “the number of gifts received from the lyricist’s true love up to and including day n in the song ‘The Twelve Days of Christmas.’” Doing that first would’ve saved me some time, but wouldn’t have been any fun.

---

Weight and measure

November 21, 2024 at 12:53 PM by Dr. Drang

Back in the summer, I decided to get more serious about controlling my Type 2 diabetes, and I enrolled in a program that I found through my insurance company. Overall, things have gone quite well: my blood glucose is down, my weight is down, and I’ve been able to cut my medications to about a third of what I was taking before.

But nothing is perfect, and the iPhone app that comes with the program (which I’ll call the “program app” here) is kind of clumsy and limited. I don’t imagine that the most talented programmers work for the company that runs this program. For example, the app monitors my weight by syncing with a smart scale, but the way it graphs the data is just silly:

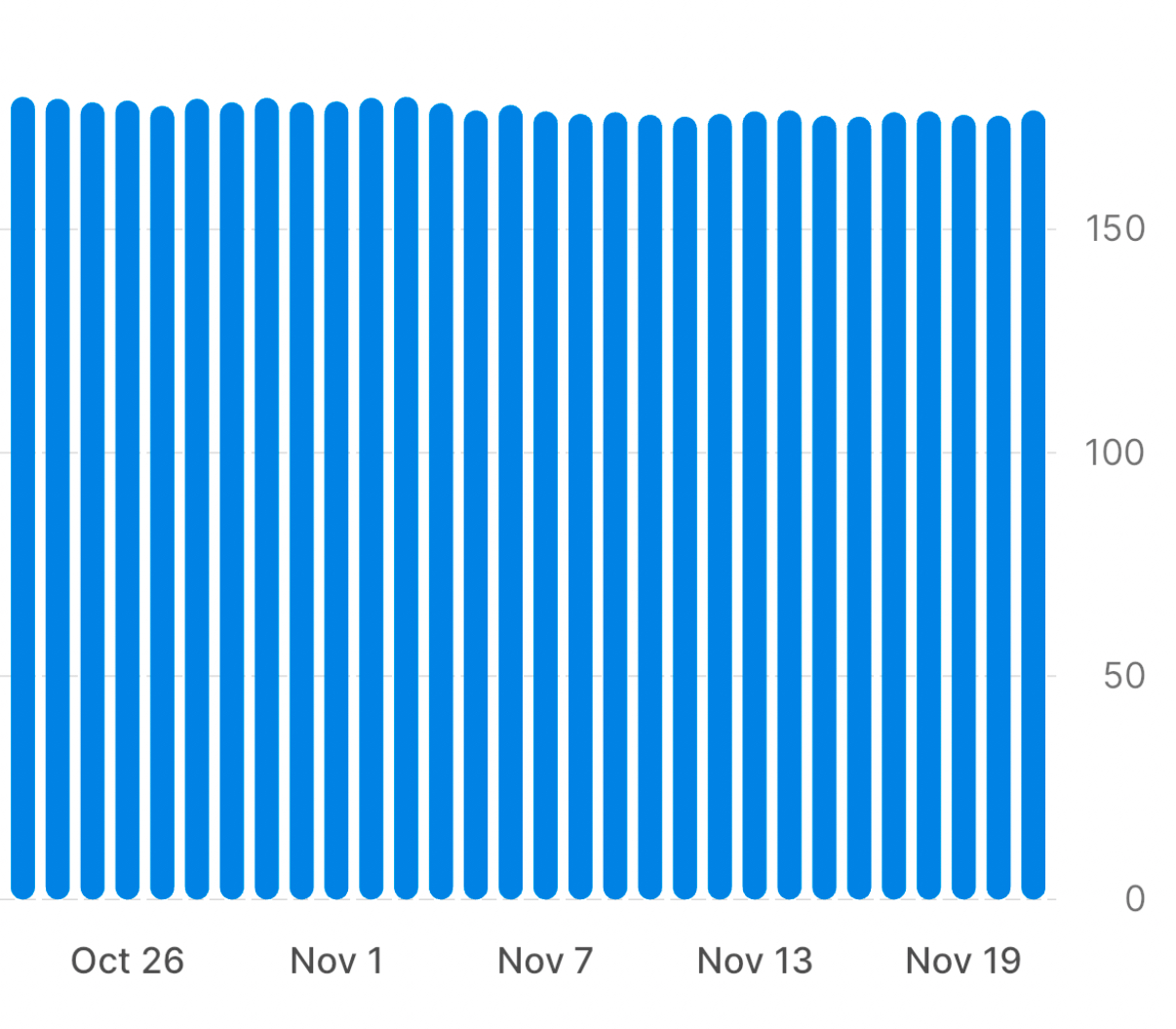
It doesn’t let you look at more than 30 days at a time, and it insists on starting the vertical axis at zero. So you can see only a narrow window of your history and all of your weight loss is jammed up at the top of the chart, making it seem like you accomplished very little.

The graph in the app is interactive, so touching on a column in the chart will show you your weight for that day, but the point of graphing data is to tell the story in the graph itself. Interactive features like that are a crutch commonly used nowadays to try to cover up for poor graph design.

What I want is something that looks like this:

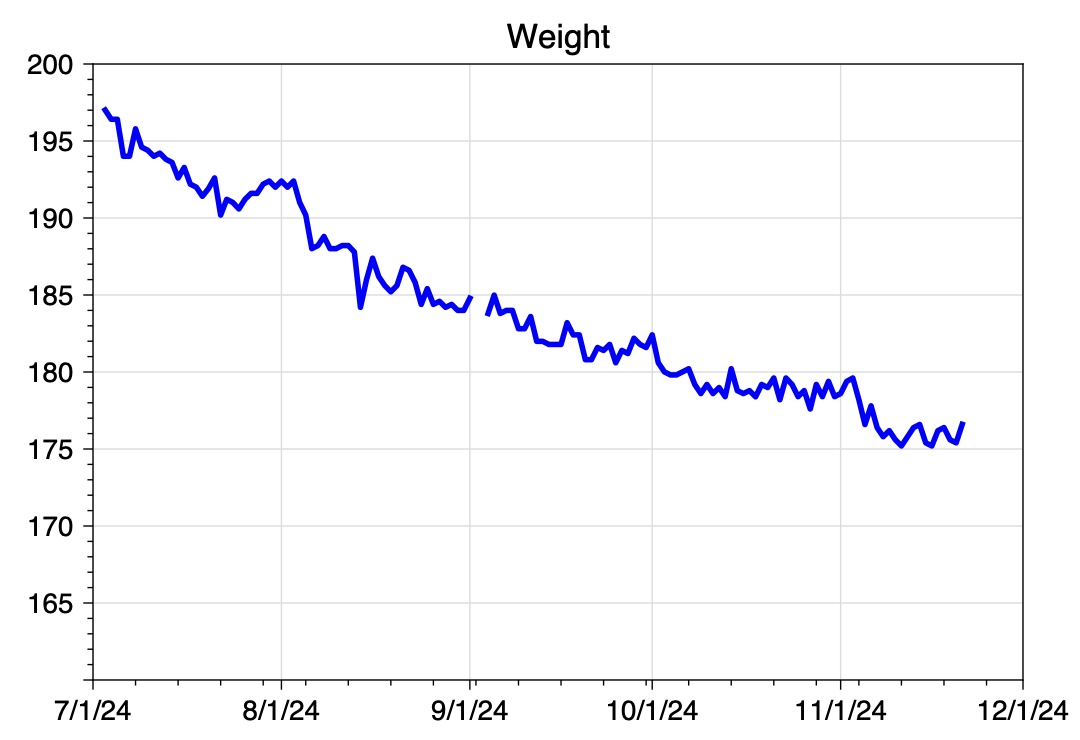
In this graph, I can see the entire scope of my time in the plan, and it looks like I’ve accomplished something. I don’t need interactivity to see where I am and where I’ve been.

As you might expect, I made this graph in Python using Matplotlib. I’ll get to the code in a minute, but first I need to talk about how I pulled the data out of the program app.

There is, of course, no export function in the app. I have a tech support question pending with the app’s developers, but I decided the likelihood of getting a satisfactory answer was small, so I went ahead and pulled the data out by hand. Or in this case, by mouth.

I paged back through my weight history, 30 days at a time, until I reached July. My plan was to use the app’s interactivity to get my weight on each day and dictate that value into a text file on my Mac, one line for each day. The plan worked, but not quite the way I expected.

I’ve written before about how well dictating numbers into my phone has worked. In this case, because I was reading the numbers off my phone, I’d have to do the dictating into my Mac, but that shouldn’t make any difference. Apple’s dictation software is the same on both platforms, isn’t it?

No. For reasons I can’t explain, the Mac doesn’t react to the commands “new line” and “new paragraph” in real time. Whenever I say “new line,” it inserts what looks like a space character and waits for me to dictate the next number. Now it’s true that after leaving dictation mode, all of those spaces turn into new lines, but because it doesn’t show what I’m saying as I say it (as it does on the iPhone), it made the dictation difficult.

So I adopted a hybrid dictation method. I dictated a number and then pressed the Return key to get a new line. After 10–15 minutes, I had a file that looked like this:

197.01
196.41
196.41
194.01
194.01
195.79
194.60
194.40
[and so on]

I then opened up a new spreadsheet in Numbers, pasted these values into the B column, and put the sequence of dates in the A column. I added a header row with “Date” and “Weight,” and exported the spreadsheet to a CSV file named weight.csv. It looks like this:

Date,Weight
2024-07-03,197.01
2024-07-04,196.41
2024-07-05,196.41
2024-07-06,194.01
2024-07-07,194.01
2024-07-08,195.79
2024-07-09,194.60
2024-07-10,194.40
[and so on]

Now we come to the Python. Here’s the code that reads the data from weight.csv and builds the graph:

python:
 1:  #!/usr/bin/env python3
 2:  
 3:  import sys
 4:  import pandas as pd
 5:  from datetime import datetime
 6:  from dateutil.relativedelta import relativedelta
 7:  import matplotlib.pyplot as plt
 8:  from matplotlib.ticker import MultipleLocator, AutoMinorLocator
 9:  from matplotlib.dates import DateFormatter, MonthLocator, WeekdayLocator, MO
10:  
11:  # Read in the weights
12:  df = pd.read_csv('weight.csv')
13:  x = pd.to_datetime(df.Date, format="%Y-%m-%d")
14:  y = df.Weight
15:  
16:  # Figure out the first day of next month
17:  today = datetime.now()
18:  nextmonth = datetime(today.year, today.month, 1) + relativedelta(months=1)
19:  
20:  # Format today's date for using in the file name
21:  today = today.strftime('%Y%m%d')
22:  
23:  # Create the plot with a given size in inches
24:  fig, ax = plt.subplots(figsize=(6, 4))
25:  
26:  # Add a line
27:  ax.plot(x, y, '-', color='blue', lw=2, label='Weight')
28:  
29:  # Set the limits
30:  plt.xlim(xmin=datetime(2024,7,1), xmax=nextmonth)
31:  plt.ylim(ymin=160, ymax=200)
32:  
33:  # Set the major and minor ticks and add a grid
34:  ax.xaxis.set_major_locator(MonthLocator())
35:  ax.xaxis.set_minor_locator(WeekdayLocator(MO))
36:  ax.xaxis.set_major_formatter(DateFormatter('%-m/%-d/%y'))
37:  plt.setp(ax.get_yticklabels()[1], visible=False)
38:  ax.yaxis.set_major_locator(MultipleLocator(5))
39:  ax.yaxis.set_minor_locator(AutoMinorLocator(5))
40:  ax.grid(linewidth=.5, axis='x', which='major', color='#dddddd', linestyle='-')
41:  ax.grid(linewidth=.5, axis='y', which='major', color='#dddddd', linestyle='-')
42:  
43:  # Title and axis labels
44:  plt.title('Weight')
45:  
46:  # Make the border and tick marks 0.5 points wide
47:  [ i.set_linewidth(0.5) for i in ax.spines.values() ]
48:  ax.tick_params(which='both', width=.5)
49:  
50:  # Add the legend
51:  # ax.legend()
52:  
53:  # Save as PDF
54:  plt.savefig(f'{today}-Weight.pdf', format='pdf')

Most of this will look familiar if you read this recent post or this one. I’ll just mention a few unique features.

First, Lines 16–21 deal with dates using a combination of the datetime and dateutil modules, the latter of which really should be in the standard library by now. This section of code uses today’s date—meaning the date on which the script is run—to figure out the upper limit of the x-axis and part of the graph’s filename. Line 18 uses dateutil’s relativedelta function to go forward one month from the first day of the current month. Although datetime has functions for certain time intervals, “one month” is not one of them, which is why I had to use dateutil.

You probably noticed that the tick marks on the x-axis are a little weird. This is an experiment, and I’m not sure yet what I think of it. The major tick marks are set on the first of every month and are labeled as such. The minor tick marks are set on the Monday of each week. This is why the frequencies of the two sets of marks aren’t in sync. The code that does this is in Lines 34–36.

Another oddity, which I definitely like, is that although the y-axis starts at 165 lbs, there’s no label for that bottom tick mark. This is handled by Line 37, which makes the label invisible. I did this because that label and the “7/1/24” label on the x-axis were too close to one another. There’s no doubt where the y-axis starts, so I figured I could eliminate it with no loss of clarity.

Finally, Line 54 saves the graph as a PDF file and uses the today variable from back on Line 21 as part of its filename. I prefer PDFs to PNGs for my own use; I used Preview’s Export command to get the PNG you see above.

As I was writing this, I got a response from the program app’s support team. As expected, there’s no way to export the weight data. Also, they think syncing the scale with two different apps is liable to cause connectivity problems, so that’s out, too. Which means that the time I took dictating my weight history was well spent. Also well spent was the few minutes it took to write this little five-step shortcut, called Weight Today. It asks me for today’s weight and adds a line to the CSV file with the date and that weight. This is a semi-automated way of keeping the weight.csv file up to date.

Step	Action	Comment
1		Get today’s date
2		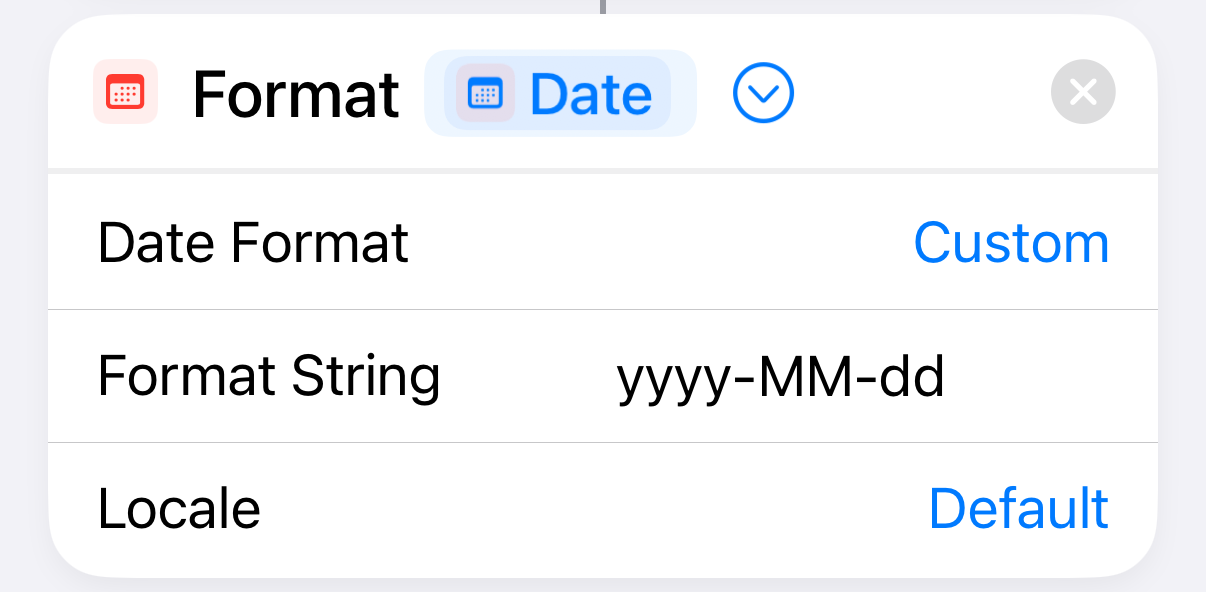Format the date as yyyy-mm-dd
3		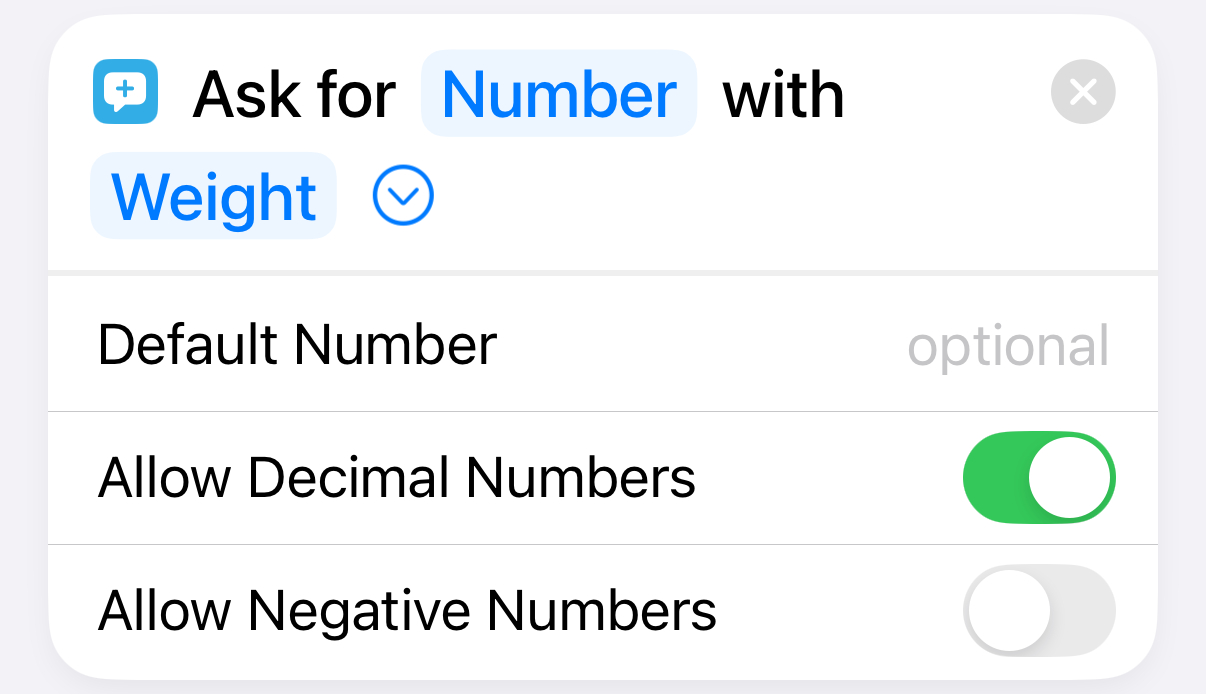Ask the user for today’s weight
4		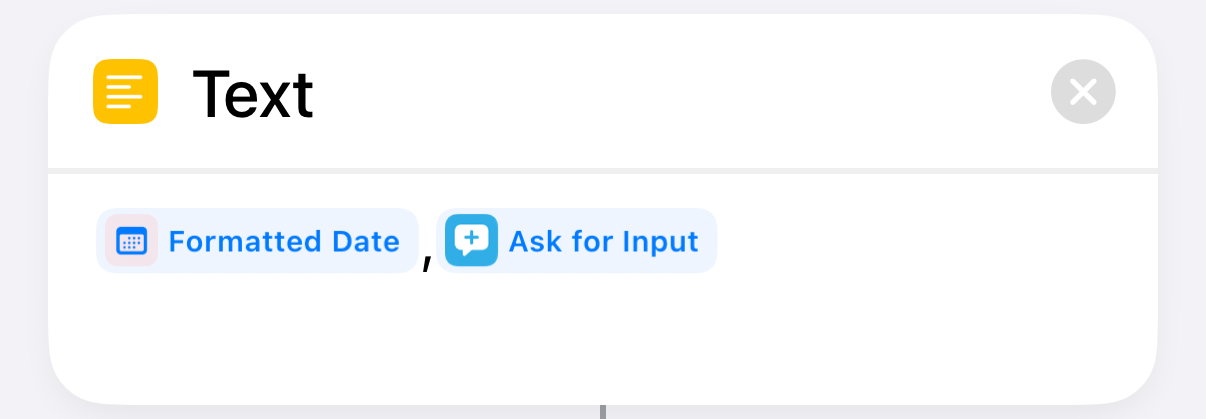Assemble the date,weight line
5		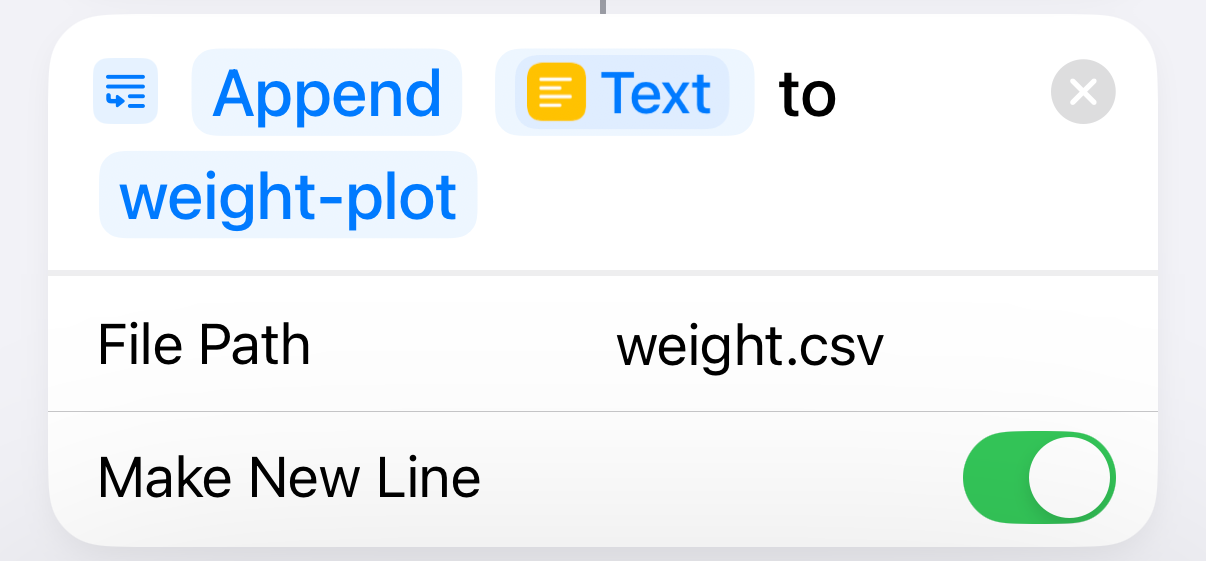Append the line to the CSV file

I’m not linking to a downloadable version of the shortcut because it has the path to the weight.csv file on my Mac built in to Step 5. It’s not hard to build yourself.

Although entering the weight myself (like an animal) isn’t my preference, I have to have the phone with me when I get on the scale to sync with the program app. So it’s only a matter of launching the shortcut, which I do from a widget on my home screen, and then typing a number. Probably takes less time than launching a dedicated smart scale app.

---

An unexpected bit of forward thinking

November 20, 2024 at 10:43 PM by Dr. Drang

I think I’ve mentioned here before that sometimes I’ll run into a computer problem and Googling for the answer leads me to a post I wrote (and forgot about) years earlier. I had a similar experience today in the physical world.

I needed to turn an electrical outlet in the spare bedroom from unswitched to switched. The room is being reconfigured, and I wanted a lamp by that outlet to be controlled by the wall switch at the door. I knew the wiring to the switch was in the outlet box because I’d changed that outlet from switched to unswitched several years ago.

As I went down into the basement to flip the circuit breaker and cut power to the outlet, I thought about my previous forays into rewiring outlets, installing ceiling fans, etc., and expected I’d have to experiment a little to figure out which breaker was on the circuit for the outlet in question. As I recalled, two of the breakers were labeled “Bedrooms,” so I had a 50-50 chance of flipping the right one first.

This certainly isn’t the biggest burden in the world, but it would mean that I have to flip one of the breakers, go from the basement to the second floor to see if the outlet was live, and then possibly repeat the process with the other breaker. I really should label those breakers more clearly, I told myself.

But when I opened the breaker box, here’s what I saw:

The large writing was done by the electrician who first wired the house some 40 years ago. The small writing is mine. Yesterday’s me had already done what today’s me planned to do by writing “South” and “North” on the labels for circuits 15 and 17. Because the outlet being changed is in one of the two north bedrooms, I cut the power to circuit 17 and had to climb the stairs only once.

Note also that yesterday’s me—on a different occasion, as evidenced by the use of a pen instead of a pencil—figured out that the lights for the basement stairs were on the same circuit as the “dinning” room. This must have taken quite a bit of experimentation, because the stairs aren’t especially close to the dining room, but at least I was able to do those experiments entirely from the basement.

So good for yesterday’s me. Not only did he preserve useful information, he wrote it down where today’s me would have to find it. Frankly, I’m kind of surprised at his forethought; yesterday’s me often thought he’d remember things that he didn’t.

---

Older posts

Site search

Meta

• drdrang at leancrew
• Blog archive
• RSS feed
• JSON feed
• Mastodon
• GitHub repositories

Recent posts

Credits

This work is licensed under a Creative Commons Attribution-Share Alike 3.0 Unported License.

© 2005–2023, Dr. Drang