Next post Previous post

Probability of failure high

January 17, 2015 at 10:15 PM by Dr. Drang

When I first heard Marco Arment’s—how shall I put this?—interesting approach to calculating the probability of failure of a system with multiple modes of failure, I decided to let it pass. It was on the most recent episode of The Talk Show, and he seemed to be speaking off the cuff, so even though what he said was wrong, it didn’t seem fair to criticize him for it. But then came this week’s ATP, and when John Siracusa spoke approvingly of it,1 I knew I had to butt in. People believe John.

The context was Marco’s “functional high ground” post. The problem with Apple’s declining software quality, he said, was that more bugs leads to a higher probability of software failure. So far, so good. Then he said the insidious thing about this is that individual failure probabilities don’t add, they multiply, which makes the failure probability of the overall system increase more than linearly with the number of bugs. No. It doesn’t work that way.

And it should be obvious that it doesn’t work that way. Probabilities are numbers less than one.2 When you multiply numbers less than one, the product is smaller than any of the individual component terms, not larger. To use Marco’s example from TTS, if you multiply 0.01 (1%) by itself three times, you get 0.000001, considerably less than 0.03.

There is actually a situation in which the probability of failure of a system is calculated by multiplying individual failure probabilities: redundant systems, the most obvious example of which is a backup generator. For a building with a backup generator to lose power, both the main power and the backup must fail. In set theory, this is an intersection of events, and the probability of an intersection is calculated through the multiplication of individual probabilities.3 But this drives the overall probability of failure down, which makes the overall system more reliable, not less. That’s why facilities have backup generators.

But Marco’s not discussing a system with backup redundancy. He’s talking about a system in which any individual failure constitutes a failure of the system. In other words, Failure A or Failure B or Failure C, etc., causes system failure. For this, we need to know how to get the probability of a union.

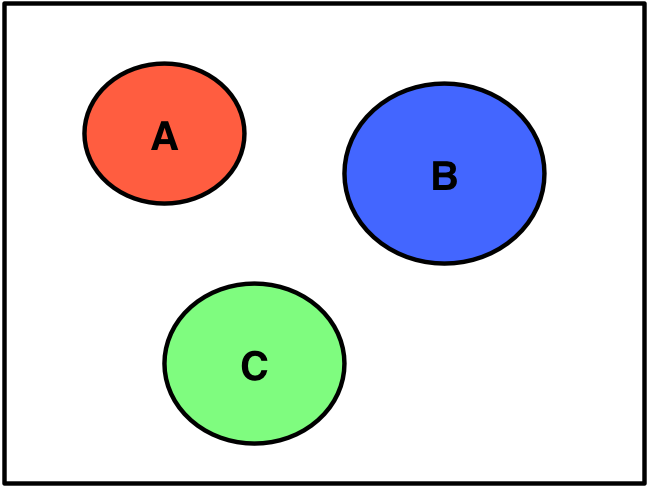
As it happens, the probability of a union can be simply the sum of the probabilities of the individual events, but that’s true only if the individual events are mutually exclusive, which means that if one occurs the others can’t occur. In Venn diagram form, mutual exclusivity looks like this:

Mutually exclusive

If the Venn diagram is drawn with the events sized according to their probabilities, the probability of the union A∪B∪CA \cup B \cup C is the sum of the red, green, and blue areas.

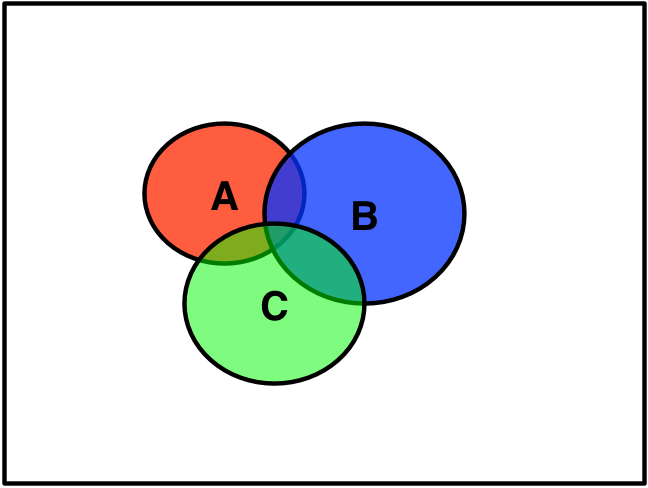
In most situations, the individual failure events are not mutually exclusive:

Not mutually exclusive

Here, the probability of the union A∪B∪CA \cup B \cup C is the area enclosed by the overall outline of the three ovals, which is less than the sum of their individual areas.

It’s this, more than the mathematical details of how to calculate probability of a union, that’s important. The probability of a union can never be greater than the sum of the individual probabilities—usually it’s less than the sum.

Let’s look at Marco’s example: Suppose we have three modes of failure, A, B, and C, each of which has a probability of 0.01. If system failure is defined as the occurrence of any of these, what is the probability of system failure?

We’ll make things easy by assuming the three modes of failure are independent. That means failure through any one of the modes has no effect on the probability of failure through the other modes. This allows us to calculate intersection probabilities by multiplication without the need for conditional probabilities.

The clever way to figure this out is to use de Morgan’s Law, which says

A∪B∪C=A¯∩B¯∩C¯―A \cup B \cup C = \overline{\bar A \cap \bar B \cap \bar C}

The overbar means complement of or, more simply, not. The probability of the complement of an event is one minus the probability of the event:

P(E¯)=1−P(E)P(\bar E) = 1 - P(E)

Therefore

P(A∪B∪C)=1−P(A¯∩B¯∩C¯)P(A \cup B \cup C) = 1 - P(\bar A \cap \bar B \cap \bar C)

and

P(A∪B∪C)=1−[1−P(A)][1−P(B)][1−P(C)]P(A \cup B \cup C) = 1 - [1 - P(A)][1 - P(B)][1 - P(C)]

So

P(A∪B∪C)=1−(0.99)3=0.0297P(A \cup B \cup C) = 1 - (0.99)^3 = 0.0297

This isn’t much less than 3%, but it is less. I wonder if Marco’s confusion about multiplication came from a hazy memory of multiplying the probabilities of the complements of failures, as we’ve done here.

Regardless, the important thing is that probability of a union is not greater than the sum of the individual probabilities, and that the probability of failure of a system doesn’t grow at a rate more than linear with the addition of more modes of failure. It grows, but at a rate less than you might expect.

Which is lucky for Apple.

Update 1/18/15 7:49 AM
Kieran Healy provides a more likely explanation for Marco and John’s confusion: the combinatorial increase in failure modes that comes from interactions between systems. As system behavior increasingly relies on components talking to one another, the number of ways the system can fail increases explosively as the number of components is increased—the rate is much greater than linear.

So while I was responding to what Marco and John said—which didn’t make sense—Professor Healy dug into what they probably meant.

  1. To his credit, on ATP Marco backed off on some of the details of what he had said on The Talk Show. ↩

  2. OK, strictly speaking, probabilities can equal one, but those are certainties. In this context, we’re not interested in certainties. ↩

  3. You may think this is true only if the two events are independent, but you still do a multiplication even if the events aren’t independent. In that case, one of the probabilities is a conditional probability. ↩

Next post Previous post