Next post Previous post

Exponentials and derviatives

April 4, 2020 at 2:57 PM by Dr. Drang

After writing this post a few weeks ago, I started a followup on other features of exponential growth. But it languished as a few disconnected paragraphs in my Drafts Inbox and on several pages of equations in a notebook. Then a friend pointed me to this video by Henry Reich, the Minute Physics YouTuber.

There’s a lot I liked in the video and a lot I didn’t like. Similarly with Aatish Bhatia’s Covid Trends interactive graph that goes along with the video.

Log-log chart of COVID-19 cases by Bhatia and Reich

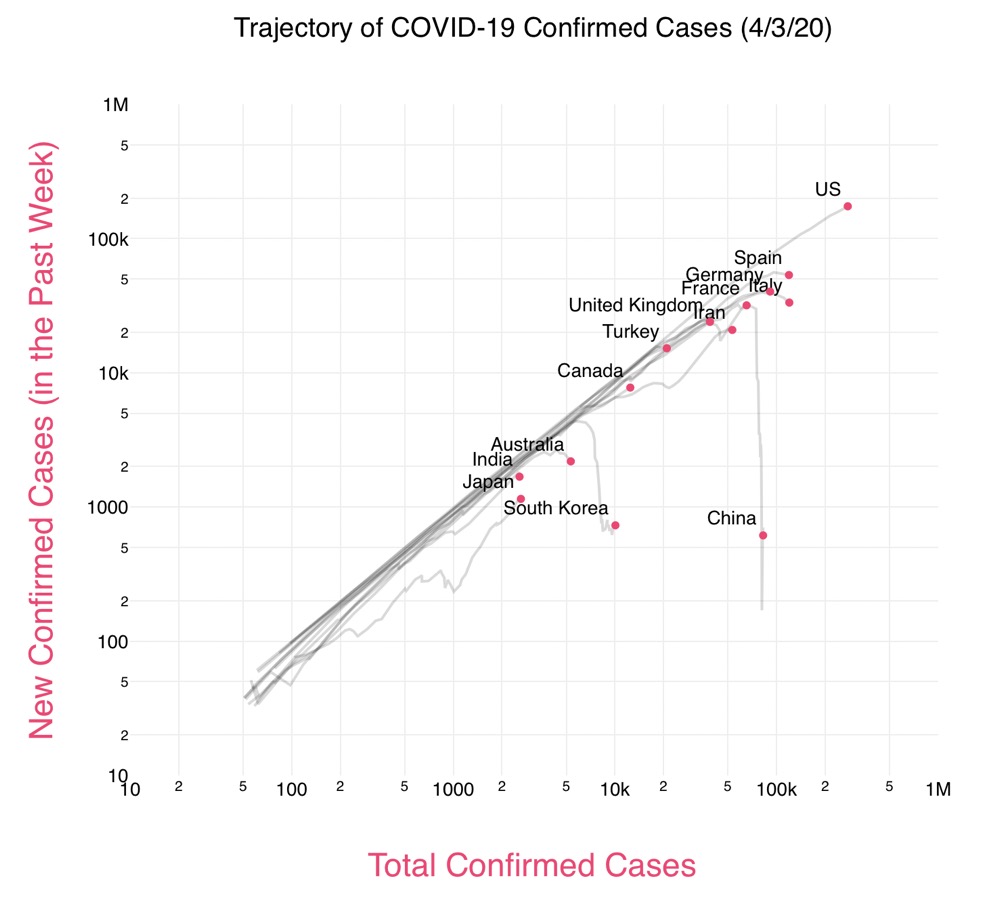
I decided to clean up my scattered notes and use Reich and Bhatia’s log-log chart as my point of focus. It might take a few posts to work my way through this, and it will definitely seem at times like I’m not focused on the log-log chart, but eventually I hope to get to a better understanding of exponential growth and how it can be represented.

Let’s start with some math. We’ll call the thing we’re keeping track of zz and if it grows exponentially with time, its value at any time tt can be represented by this equation:

z=z0eβtz = z_0\, e^{\beta t}

where z0z_0 is the value of zz at time t=0t = 0 and β\beta is a parameter that determines the rapidity of the growth.

Applying a little dimensional analysis, we see that z0z_0 must have the same units as zz, so if the units of zz is confirmed cases of COVID-19, so will be the units of z0z_0. The units of β\beta might seem unusual to you. Because the exponent has to be dimensionless—a pure number with no units—the units of β\beta must be the reciprocal of the units of tt. So if we’re measuring tt in days, we have to measure β\beta in days−1\mathrm{days}^{-1}. Similarly, if we’re measuring tt in weeks or months, we have to measure β\beta in weeks−1\mathrm{weeks}^{-1} or months−1\mathrm{months}^{-1}. As we said last time, taking the logarithm of both sides of our exponential equation gives us

logz=ln(z0eβt)=βt+logz0\log z = \ln \left( z_0\, e^{\beta t} \right) = \beta\, t + \log z_0

which is the equation of a straight line with slope β\beta if we graph zz vs. tt on a semilog plot. To avoid concerns about dimensions (what are the units of logzlog z?), it might be better to think of this relationship as

log(zz0)=βt\log \left(\frac{z}{z_0} \right) = \beta\, t

so we have pure numbers on each side of the equation. The line on a semilog plot now goes through the origin but still has a slope of β\beta.

(I’m being a little handwavy with regard to the base of the logarithm. Typically, we don’t use a natural log scale in a semilog plot, so the slope of the semilog plot would be betabeta multiplied by a scale factor. If we’re using base-10 logs in our plot [the most common case], the scale factor is log10e\log_{10} e.)

(And while I’m being parenthetical, I’ll mention that engineers typically use ln\ln to mean natural logs and log\log with no subscript to mean base-10 logs, mathematicians, computer scientists, and most programming languages use log\log (or log())to mean natural logs and log10\log_{10} (or log10()) to mean base-10 logs. I’m going to go against my instincts here and use the math/computer terminology because it will fit in better with any scripts we develop.)

One of the cool features of the exponential function is that its derivative is also exponential.

dzdt=z˙=ddt(z0eβt)=βz0eβt\frac{dz}{dt} = \dot{z} = \frac{d}{dt} \left( z_0\, e^{\beta t} \right) = \beta\, z_0\, e^{\beta t}

where I’ve used the common notation (inherited from Newton) of a dot to represent differentiation with respect to time.

Since the derivative is an exponential function, that means it too will appear as a straight line on a semilog plot. By extension, we can keep taking derivatives as long as we like and never change the fundamental nature of the result. It’s exponentials all the way down.

This is all very well and good for functions, but what does it mean for plotting data we suspect is exponential? It means that we can not only graph the cumulative value, zz, on a semilog plot and see if it appears as a straight line, we can also plot the daily (or weekly or monthly) change in zz and see if it graphs as a straight line on a semilog plot, too. For the COVID-19 data, the daily change has the units of cases per day, which is exactly the kind of units we would expect for a derivative.

It’s the use of daily data that’s the first step in Bhatia and Reich’s approach. I started doing the same thing a few days ago with the US data from the COVID Tracking project. Here’s a comparison of the cumulative and daily data for confirmed cases.

Cumulative and daily cases

These clearly aren’t linear over the entire month, although the cumulative cases look pretty linear in the first half of March. I’ve added a locally-weighted regression line (lowess) to give your eye a path to follow through the scatter.

One thing you probably noticed right away was that the daily graph is more noisy than the cumulative one. That’s normal for real data—the process of accumulation tends to smooth out short-term variations.

Another thing to notice is that changes in direction tend to be sharper in the daily plot, which makes them easier to see. The bend that starts around March 20 is certainly more distinct in the daily plot. That’s one of the things Reich and Bhatia take advantage of in their log-log plot.

With the mathematical preliminaries out of the way, we’ll start the next post looking at other ways to plot the cumulative and daily data. In particular, we’ll look at Reich and Bhatia’s log-log plot of daily vs. cumulative and see what advantages it presents. We’ll also see whether we lose information in plotting the data that way. (Spoiler: yes.)

Next post Previous post