Some bc stuff
February 22, 2021 at 11:31 PM by Dr. Drang
When I sit down at my computer to do a longish series of calculations, I open a Jupyter console session. That gives me an interactive Python environment with all of NumPy and SciPy at my disposal. But when I just want to do a quick little calculation or two, the time it takes to start up Jupyter gets in the way. That’s when bc comes in handy.
I don’t know why bc is named bc. The c part is obviously “calculator,” but I’m not sure what the b is for—”basic,” maybe? It was originally a front end for the older dc (“desk calculator”), but the GNU version, which is what we have on our Macs, is a standalone program.
Update Feb 23, 2021 2:05 PM
According to this page, the b stands for “Bell,” which seems plausible.
Update Feb 22, 2021 2:24 PM
Kevin Likes remembers that where he went to school the b was thought to be “bignum.” Also plausible, since one of the bc’s main features is its ability to do math at arbitrarily large precision.
If anyone knows Lorinda Cherry, can you ask her?
I used to think bc was useless—I don’t trust a calculator that tells me 1/2 = 0—but I changed my mind after seeing what John Cook has done with it (here’s a good example). Although its defaults are weird, bc is quite nice if you start it up the right way, which is
bc -lq
where the -l option tells it to load in it small library of functions and sets the scale parameter (which controls the number of digits after the decimal point) to 20, and the -q option tells to start up without printing out the copyright information. Rather than remembering to type this every time, I have an alias in my .bashrc file:
alias bc='bc -lq'
I said bc has a small library of functions, and I wasn’t kidding. Here they are:
| bc function | math function |
|---|---|
| s(x) | sine |
| c(x) | cosine |
| a(x) | arctangent |
| l(x) | natural log |
| e(x) | exponential |
| j(n, x) | nth Bessel function |
The more time you spend with Unix, the more you realize how much the folks from Bell Labs hated typing.
I like terse commands, too, but I think bc goes too far. Also, I prefer having a tangent function to constantly dividing sine by cosine. So I have a dotfile in my home directory, .bc, that defines the common names for the standard functions and adds a few more to make my life easier. Here it is:
1: # Trig
2: pi = 4*a(1)
3: define deg(x) { return 180*x/pi }
4: define rad(x) { return pi*x/180 }
5:
6: define t(x) { return s(x)/c(x) }
7: define sin(x) { return s(x) }
8: define sind(x) { return s(rad(x)) }
9: define cos(x) { return c(x) }
10: define cosd(x) { return c(rad(x)) }
11: define tan(x) { return t(x) }
12: define tand(x) { return t(rad(x)) }
13: define atan(x) { return a(x) }
14: define atand(x) { return deg(a(x)) }
15:
16: define asin(x) {
17: if (x == 1) {
18: ans = pi/2
19: } else {
20: if (x == -1) {
21: ans = -pi/2
22: } else {
23: ans = a(x/sqrt(1 - x^2))
24: }
25: }
26: return ans
27: }
28: define asind(x) { return deg(asin(x)) }
29:
30: define acos(x) {
31: if (x == 0 ) {
32: ans = pi/2
33: } else {
34: if (x > 0) {
35: ans = a(sqrt(1 - x^2)/x)
36: } else {
37: ans = a(sqrt(1 - x^2)/x) + pi
38: }
39: }
40: return ans
41: }
42: define acosd(x) { return deg(acos(x)) }
43:
44: # Exponential
45: define exp(x) { return e(x) }
46: define log(x) { return l(x) }
47: define ln(x) { return l(x) }
48: define log10(x) { return l(x)/l(10) }
49: define log2(x) { return l(x)/l(2) }
Most of this is pretty obvious, but a few comments are in order:
- The arcsine and arccosine functions are defined to avoid division by zero errors when their arguments are 1, -1 (for
asin), or 0 (foracos). - In keeping with the usual definitions,
asinreturns an angle between π/2 and -π/2, andacosreturns an angle between 0 and π. - Old Fortran programmers (are there any other kind) will recognize the “degree” versions of the trig functions. Measured angles are always given in degrees, and it’s more convenient to have functions that work with those kinds of arguments.
- Old habits die hard, and although I know that
logis the natural logarithm in every programming language, I still sometimes typeln. So I added a function that allows me to keep making that mistake without punishment.
To get these definitions loaded into bc, I have this line in my bashrc:
export BC_ENV_ARGS=$HOME/.bc
BC_ENV_ARGS is a poorly named environment variable that tells bc to run the given file on startup. With this definition and the alias mentioned above, whenever I type bc at the command line, I get all of these functions and 20 decimal places of precision.
If I ever feel the need for more functions, this page has quite a few.
One last thing. When you don’t give it a file name argument, bc goes into interactive mode. This is nice when you have a few calculations to do, but it does force you to quit bc when you’re done (which you can do with either the quit command or by typing ⌃D). If you have just one calculation to do, it’s faster to give bc the command through a here string, like this:
bc <<< "5*cos(35) - 5*sin(35)"
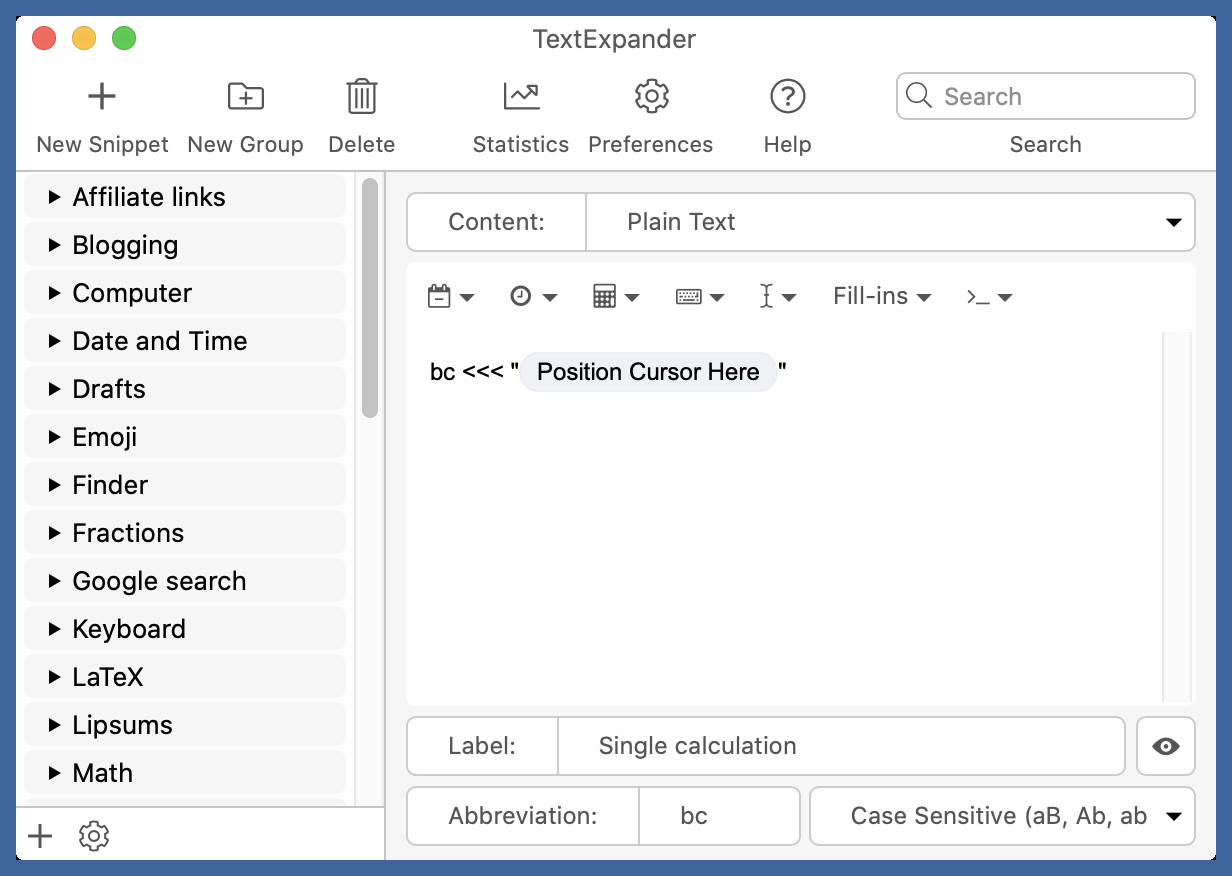
Of course, like the Bell Labs people, I’m far too lazy to type out all those less than signs, and I can never remember to type the opening quotation mark before the calculation. So I made a TextExpander snippet that types out the boilerplate and puts the cursor between the quotation marks. All I have to type is the calculation itself.