Next post Previous post

Cutting the cord

July 31, 2021 at 9:55 AM by Dr. Drang

You may have seen Steve Mould’s recent video, called “The Spring Paradox.” If not, take a few minutes, and we’ll reconvene when you’re done.

As you might expect, I’m not interested in the traffic problem that takes up the second half of the video. But the spring problem that gives the video its name is cute, and Mould does a good job explaining how the behavior is related to the difference between springs in series and springs in parallel. But…

Surely the weight won’t rise under all conditions. If the two longer strings, the red and green ones, were much longer—or if the springs were much stiffer—the weight would drop. So what restrictions did Mould have to adhere to when he set up his demonstration?

Let’s start by drawing the two states next to one another. Before cutting is on the left and after cutting is on the right.

Springs and strings from Mould video

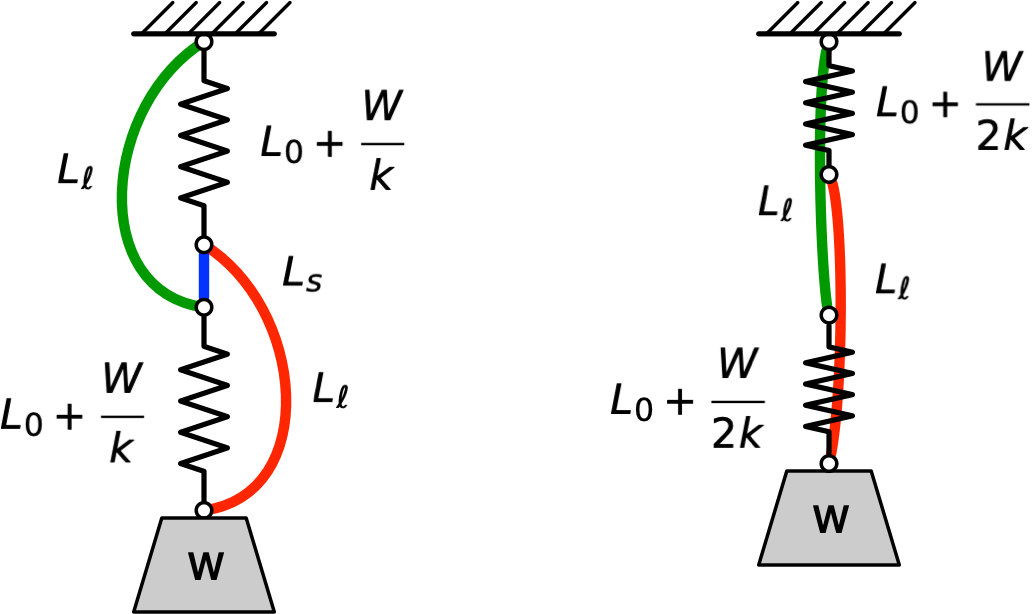
(The strings should be straight on the right, but I’ve drawn them curved so they don’t overlap.)

Our starting assumptions are:

  1. All the strings are inextensible.
  2. The long red and green strings are the same length, L ℓ.
  3. The short blue string is of length L s.
  4. The springs have the same unstretched length, L 0.
  5. The springs follow Hooke’s Law and have the same stiffness, k.

Recall that Hooke’s Law says that the stretch in a spring, x is related to the force acting on it, F, through the simple linear relationship

F=kx

Strictly speaking, we could relax the last condition and say only that the two springs must have the same force-deflection relationship. It doesn’t have to be a linear relationship, but that will make the algebra easier.1

In the “before” state, each spring is carrying a the full weight, W, and is stretched a distance Wk. Therefore, the distance between the ceiling and the weight is

2(L 0+Wk)+L s

where L s is the length of the short blue string.

In the “after” state, each spring is carrying half the weight, and is stretched a distance W2k. Therefore, the distance between the ceiling and the weight is

L ℓ+(L 0+W2k)

For the weight to go up when the blue string is cut, we must have

L ℓ+(L 0+W2k)Unknown character2(L 0+Wk)+L s

or, after some algebra,

L ℓUnknown characterL 0+L s+32Wk

This sets the upper bound on the lengths of the red and green strings if we want the weight to behave as it does in the video. If the strings are longer than this, the weight will go down when the blue string is cut.

There’s also a lower bound on L ℓ. The problem starts with slack in the red and green strings, so

L ℓUnknown character(L 0+Wk)+L s

Putting the two restrictions together, we have

L 0+L s+WkUnknown characterL ℓUnknown characterL 0+L s+32Wk

So to get the behavior we see in the video, the lengths of the red and green strings have to be within a range of

12Wk

In the video, this is a relatively long range, because the springs are pretty stretchy. But if the strings were stiff, you’d have to be quite precise in setting their lengths. In the limit as k→∞, which is what we’d see if we replaced the springs with inextensible strings, upward movement would be impossible—we can’t achieve both inequalities.

This, I suspect, is part of the reason the behavior seems weird to us. When we see the initial setup, our brains tend to think of the springs as being of a particular length that won’t change. We don’t expect them to shorten by more than the amount of slack in the red and green strings. Maybe if we had seen the springs at their unstretched length before the video started, we wouldn’t be as surprised to see them contract and the weight move up.

One last calculation: how much does the weight move up? Subtracting the “after” length from the “before” length gives us

y=[2(L 0+Wk)+L s]−[L ℓ+(L 0+W2k)]

which is

y=L 0+L s−L ℓ+32Wk

Solving this equation for L ℓ and substituting into the inequality above gives us

L 0+L s+WkUnknown characterL 0+L s+32Wk−yUnknown characterL 0+L s+32Wk

After some cancellation, we get

−12WkUnknown character−yUnknown character0

which, after multiplying through by -1 and flipping the inequality signs, gives us

0Unknown characteryUnknown character12Wk

Is it a coincidence that the upper bound here is the same as the range of string length we calculated earlier? What do you think?

To get the most upward movement, we’d like the red and green strings to be at the short end of their range. But without much slack in the strings, the trick wouldn’t look as cool. The way to get a noticeable upward movement and significant slack in the strings is to use a stretchy spring, which is exactly what Mould does. Clever guy.

  1. In fact, as Mould points out, his springs are being stretched enough to act outside their linear range. The trick still works, but not exactly according to the calculations we do below. ↩

Next post Previous post