Next post Previous post

Orbital curvature

October 16, 2022 at 9:11 PM by Dr. Drang

Last week, John Cook wrote a nice post on the shape of the Moon’s orbit. He was inspired by a paper written by Noah Samuel Brannen for the College Mathematics Journal back in 2001.1 The gist of their analyses is that if you trace out the Moon’s path as it and the Earth travel around the Sun, you will find—probably to your surprise—that the shape you get is convex everywhere. Even when the Moon is new, and it’s between the Earth and the Sun, its path is still bending toward the Sun and not toward the Earth.

As it happens, I was not surprised to see this. I first read about it in one of Isaac Asimov’s science books back when I was a teenager. It’s stuck with me all these years, mainly because I didn’t really understand it and couldn’t visualize it. But after reading Cook and Brannen and fiddling around in Mathematica, I finally get it, some 45 years later.

Because the orbits of both the Moon and the Earth have low eccentricities, we can model them both as circles. Using Brannen’s coordinate system, with the origin at the Sun, the x and y position of the Moon can be expressed in parametric form as

x(θ)=dcosθ+cospθx(\theta) = d \cos \theta + \cos p\, \theta y(θ)=dsinθ+sinpθy(\theta) = d \sin \theta + \sin p\, \theta

where we have taken the radius of the Moon’s orbit to be 1, and

With this coordinate system, xx and yy are measured not in miles or kilometers, but in multiples of the Moon’s orbital radius. That may seem weird, but it’s often convenient to put things in nondimensional form like this.

Mathematica knows the orbital radii of the Earth and Moon so we can get the value of dd via

 d = Entity["Planet", "Earth"]["AverageOrbitDistance"] /
     Entity["PlanetaryMoon", "Moon"]["AverageOrbitDistance"]

which is 388.6. Similarly, we can get the orbital periods of the Earth and Moon using

TEarth = Entity["Planet", "Earth"]["OrbitPeriod"]

which gives 365.25636 days, and

TMoon = Entity["PlanetaryMoon", "Moon"]["OrbitPeriod"]

which gives 27.322 days. Thus,

p = TEarth / TMoon

is 13.369.

You may be questioning these numbers. After all, doesn’t the Gregorian calendar tell us a year is about 365.2425 days long?2 And isn’t the time between new moons more like 29½ days? Yes, but these common values are from an Earth-centric frame of reference. The values we need for our equations are the sidereal (relative to the stars) values. Luckily, Mathematica gives us the sidereal figures, rather than the tropical year (365.2422 days) or the synodic month (29.53 days).

So if we plug these values in for dd and pp and plot out a year’s worth of Moon positions, we get this shape:

One year of moon orbit

This is roughly a circle, but you can see the waviness. It’s an SVG image, so you can zoom in as far as you like. Or you can look at this section of the path, where I’ve added a blue dashed line to represent the Earth’s orbit.

Section of moon and earth orbit

This certainly looks like a convex figure, but how can we be sure? Brannen does so by investigating the curvature of the path. If the curvature is positive throughout the path, the curve is convex.

(If you’re wondering—as I was—why that’s so, go back to the definition of curvature. Curvature is the rate of change of direction of a line tangent to the path with movement along the path. In our situation, the Moon is moving counterclockwise along the red path in the figure above. If the tangent to the path is rotating counterclockwise as the Moon moves, then the path is convex—it’s always bulging outward.)

Mathematica has a function, ArcCurvature, that I thought would do what I wanted without fiddling with all the individual derivatives. But while ArcCurvature does return the curvature for a curve expressed in parametric form, it gives the unsigned curvature. So instead of taking a Mathematica shortcut, we have to go the long way around.

For a path defined parametrically, the curvature is

κ=x′y′′−y′x′′(x′2+y′2)3/2\kappa = \frac{x^{\prime} y^{\prime\prime} - y^{\prime} x^{\prime\prime}}{\:\:\left({x^{\prime}}^2 + {y^{\prime}}^2 \right)^{3/2}}

where the primes indicate differentiation with respect to θ\theta.

Because the denominator is the power of a sum of squares, it’s always positive. So the sign of κ\kappa depends on the sign of the numerator. For our parametric equations, the numerator works out to be

d2+p3+dp(p+1)cos(1−p)θd^2 + p^3 + d\,p\,(p+1)\, \cos (1 - p) \theta

Since cosine can’t be less than –1, the smallest this expression can be is

d2+p3−dp(p+1)d^2 + p^3 - d\,p\,(p+1)

which factors to

(d−p)(d−p2)(d - p) (d - p^2)

Looking back at our values for dd and pp above, it’s clear that both of these terms are positive, so our curvature is positive for all values of θ\theta. Hence, the Moon’s path around the Sun is convex.

Let’s move on to Isaac Asimov. What he did that’s stuck with me all these years is compare the gravitational pull of the Sun on the Moon to the gravitational pull of the Earth on the Moon. He started with Newton’s Law of Gravitation,

F=Gm1m2r2F = \frac{G \, m_1 \, m_2}{r^2}

and compared the force associated with the Moon/Sun system to that of the Moon/Earth system. The ratio, after the common terms drop out, is

mS/mE(rS/rE)2\frac{m_S/m_E}{\left( r_S/r_E \right)^2}

where

You’d be hard-pressed to find a reference with a table that gives you the mean distance from the Moon to the Sun, but it is, of course, the same as the orbital radius of the Earth. So the ratio in the denominator is just the value of dd we were using in our earlier calculations.

The mass ratio can be calculated from Mathematica’s built-in data:

mRatio = Entity["Star", "Sun"]["Mass"] /
         Entity["Planet", "Earth"]["Mass"]

which works out to 3.329×1053.329 \times 10^5. The force ratio, then, is

3.329×105388.62=2.2\frac{3.329 \times 10^5}{388.6^2} = 2.2

In other words, the Sun exerts more than twice as much gravitational force on the Moon as the Earth does. Asimov argued that this means the Moon is really orbiting the Sun, with some perturbation by the Earth, and that’s why the Moon’s path looks like a slightly wobbly circle around the Sun.

But Asimov didn’t get into the kind of detail about the Moon’s orbit the way Cook and Brannen did, so I had a hard time getting this image of its path—which comes from Brannen’s paper—out of my head.

Incorrect lunar path

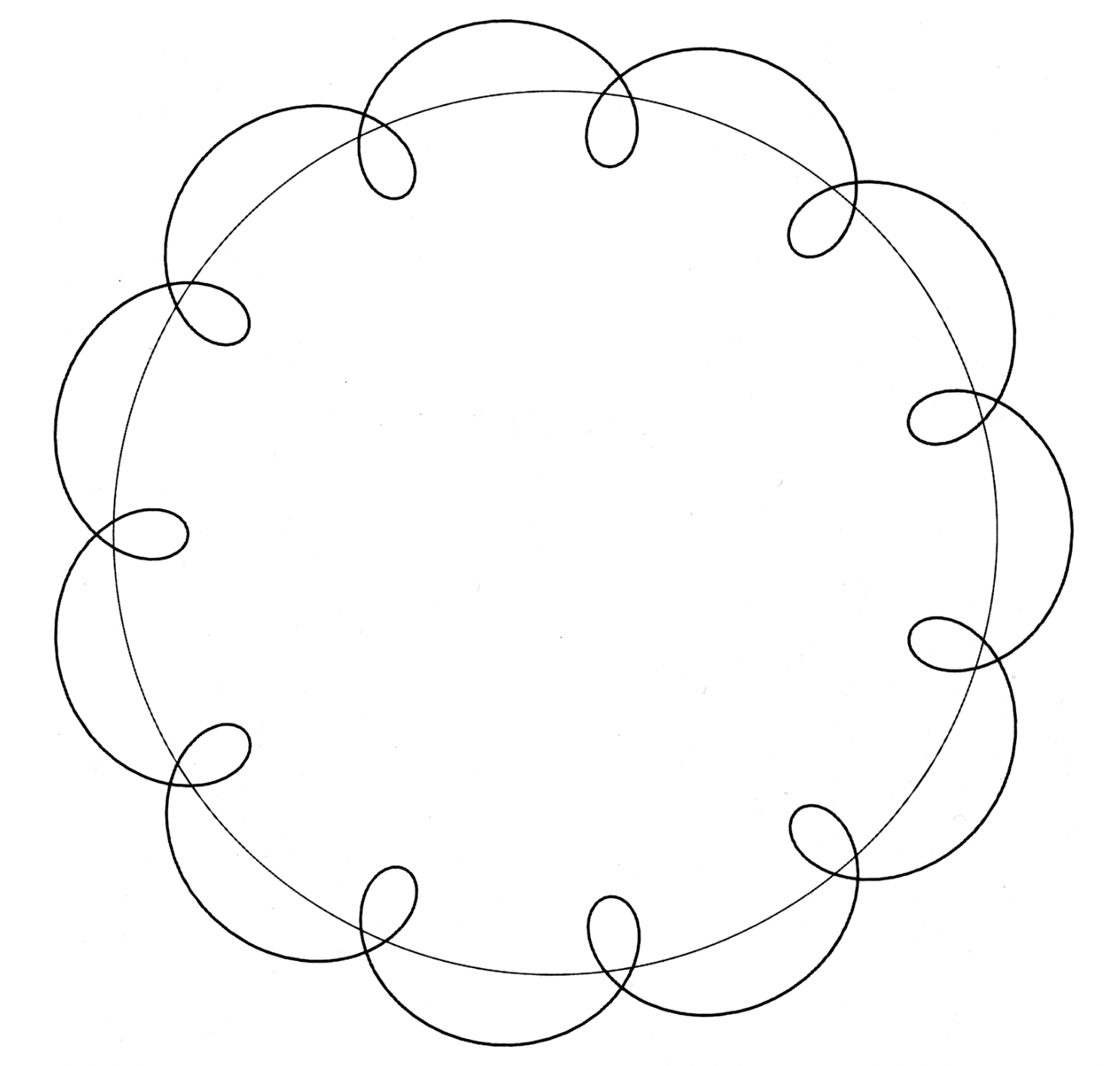
Now I know better.

I was going to leave it there, but curiosity got the better of me. I wanted to find the Asimov book with this material and see if my memory was right.3 I knew that the book was one of his collections of science essays, probably a collection of his monthly columns in The Magazine of Fantasy and Science Fiction. Because these collections were often themed and given titles like Asimov on Something, I searched for Asimov on Astronomy.

I got a hit right away. The Internet Archive has a scan of the book, and Chapter 9, “Just Mooning Around,” has the stuff I remembered, although he calculated the force ratio the other way around, with the force of the Earth on the Moon being 0.46 that of the Sun. Here’s his conclusion:

We might look upon the Moon, then, as neither a true satellite of the Earth, nor captured one, but as a planet, in its own right, moving about the Sun, in careful step with the Earth. To be sure, from within the Earth-Moon system, the simplest way of picturing the situation is to have the Moon revolve about the Earth; but if you were to draw a picture of the orbits of the Earth and Moon about the Sun, exactly to scale, you would see that the Moon’s orbit is everywhere concave toward the Sun. It is always “falling” toward the Sun.

Asimov on Astronomy came out in 1974. The “Just Mooning Around” column was first published in the May 1963 issue of F&SF and had been previously collected in Of Time and Space and Other Things. Since I was being a completist, I grabbed the magazine cover image from the Internet Speculative Fiction Database.

FSF 1963-05 cover

This is what the internet is for.

  1. The DOI of Brannen’s paper is 10.1080/07468342.2001.11921888, so those of you with accounts at academic libraries can use that to get a copy. The rest of us can use Sci-Hub (whose home page may have moved by the time you read this). ↩

  2. That’s 365 days in a normal year, plus one for every leap year (0.25), minus one for three out of every four century years (0.0075). ↩

  3. Since I’ve added this section, it’s a good bet that it was. ↩

Next post Previous post