Next post Previous post

Simplifying trig expressions

November 1, 2022 at 9:43 AM by Dr. Drang

When using any computer algebra system, there comes a time when you wonder why the result produced by the program isn’t as simple as you could make it by hand. To get good at using such a system, you have to learn its tricks of substitution and simplification.

Quite often, the results seem more complicated than they should because you carry in your head certain underlying assumptions about the nature of the variables that you haven’t told the program about.

For example, I’ve seen Mathematica return this,

r2\sqrt{r^2}

which seems weird until you realize that it doesn’t know that rr is a postive—or at least nonnegative—number. But if I add this at the top of the notebook,

$Assumptions = r ≥ 0

Mathematica does what I expect and simplifies the root to just rr.

Once I learned about $Assumptions, and the related Assuming function and Assumptions option, I got more of the results I was expecting from Mathematica. But I’m still struggling with trigonmetric simplifications. Over the weekend, I was doing a definite integral, and got a result that included this term:

ArcTan[Cot[θ]]

First, I was a little surprised to see cotangent, a function I haven’t used since high school (or maybe even junior high). For whatever reason, the mathematical derivations I’ve seen since college have eschewed the upside-down trig functions—secant, cosecant, and cotangent—in favor of dividing by their “regular” counterparts. The only exception I can think of is the secant formula for eccentrically loaded columns.

Anyway, there certainly has to be a simpler way of expressing the arctangent of the cotangent of an angle. I tried everyone’s first line of defense, Simplify, and just got ArcTan[Cot[θ]] back. I then tried TrigExpand, TrigReduce, and TrigFactor without much hope of success, as they’re geared toward rewriting powers of trig functions and trig functions applied to multiple angles. I got what I expected: still just ArcTan[Cot[θ]].

It didn’t take too much thought to get the simplified answer I was looking for: the complement of θ\theta. Consider this plot of tangent (blue) and cotangent (red) in the first quadrant.1

Tangent and cotangent

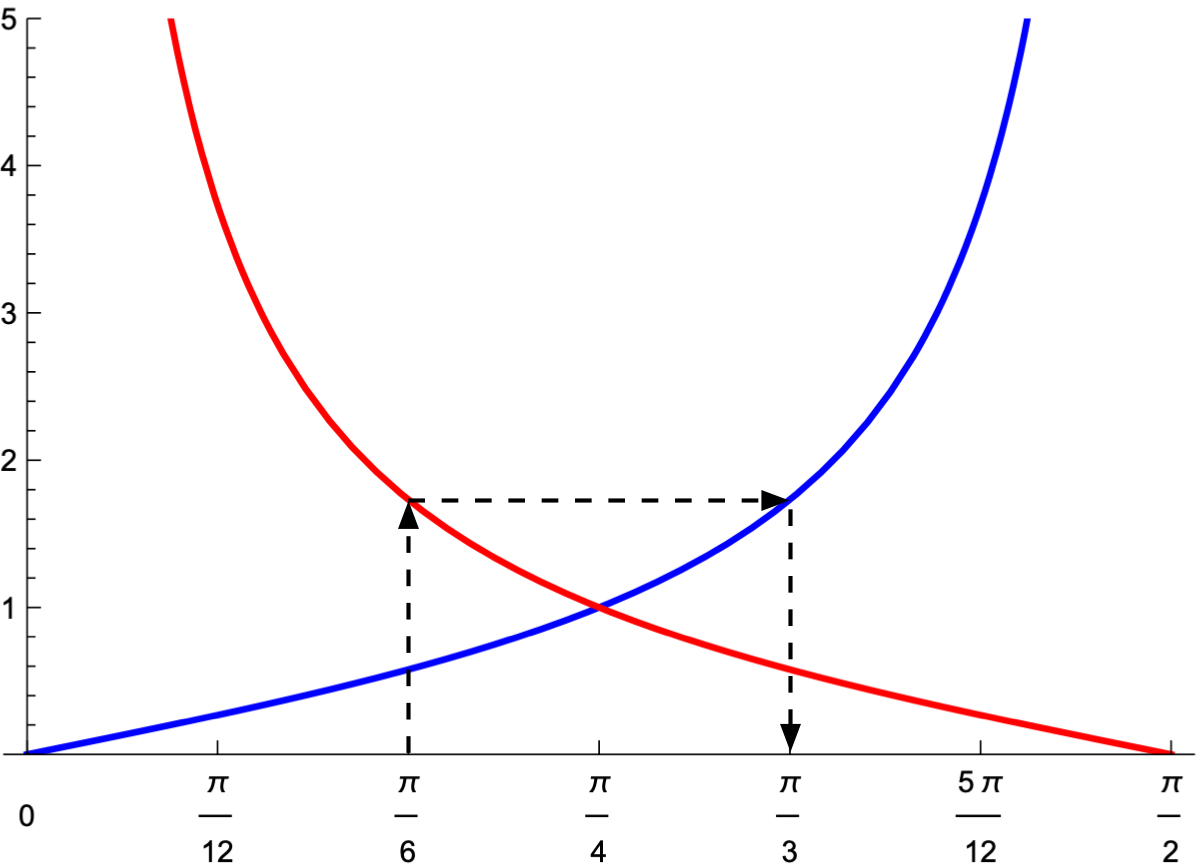
They are mirror images of each other about π/4\pi/4. So if we start at some angle, say π/6\pi/6, on the horizontal axis and go up to the red line, we’ll get its cotangent. Running horizontally over to the blue line gives us the arctangent of that value, which we read by dropping back down to the horizontal axis. Because of the mirror symmetry, we end up at the complement of our starting angle. Or, in algebraic terms,

tan−1(cotθ)=π2−θ\tan^{-1}(\cot \theta) = \frac{\pi}{2} - \theta

Of course, I didn’t get this result through Mathematica, I got it through thinking.

I was able to use Mathematica to confirm this result, but it was by a roundabout path. I plotted ArcTan[Cot[θ]] over the first quadrant and got what looked like a nice straight line.

ArcTan of Cot

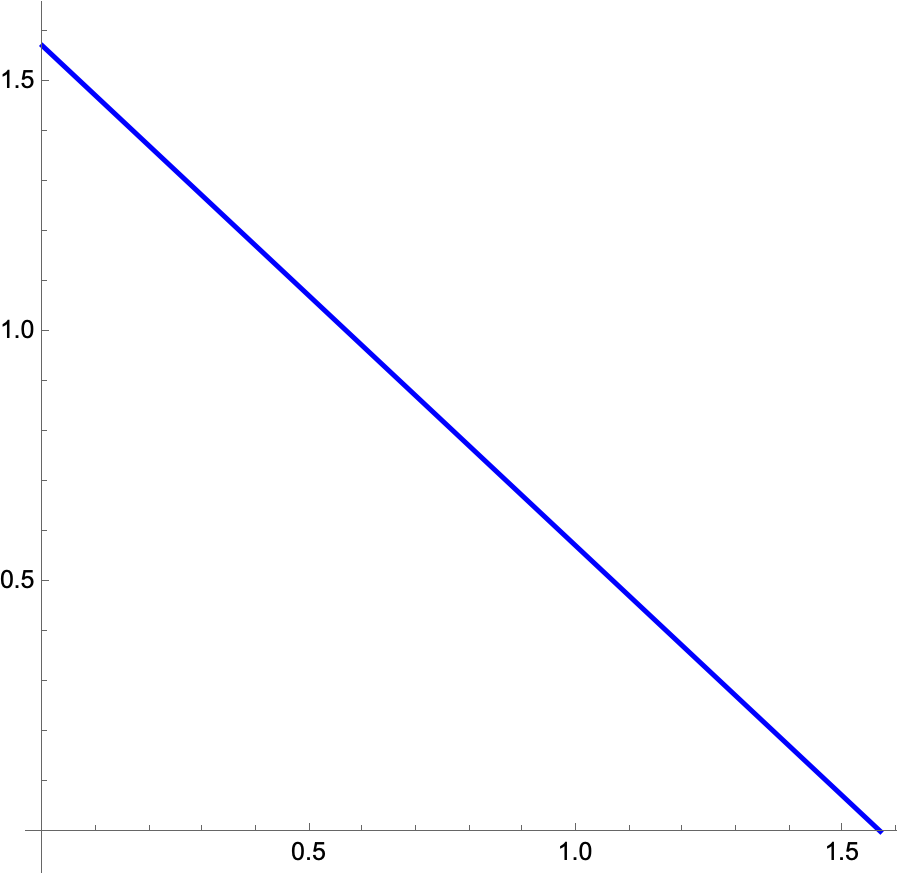
If it is a straight line, the slope should be –1 everywhere. To check this, I took the derivative:

Derivative in Mathematica

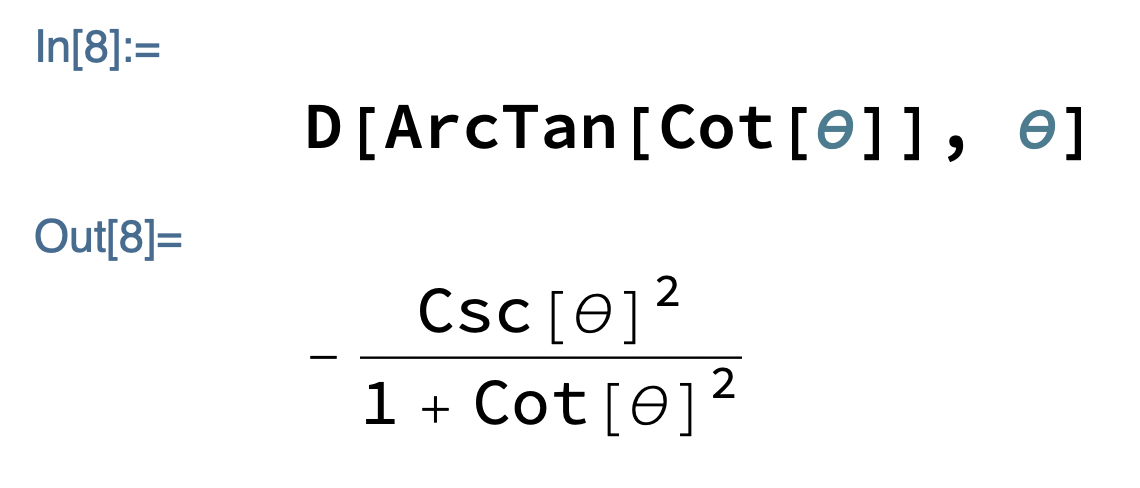
Come on, Mathematica, you can do better than that. I applied TrigFactor to the result and (finally) got –1. The y-intercept looks like it’s at π/2, which I confirmed through

Intercept in Mathematica

I couldn’t just plug in 0 for θ, because the cotangent of 0 is undefined. And I had to use a directional limit, because the limit from below goes to –π/2.

Although I got Mathematica to confirm that ArcTan[Cot[θ]] is π/2 – θ, I never got it to give me that answer itself. Maybe that’s because Mathematica thinks ArcTan[Cot[θ]] is a superior answer; more likely, it’s because I haven’t been using it long enough to know its tricks.

  1. The physical problem I was dealing with meant the angle was always going to be in the first quadrant—between 0 and π/2 radians or 0° and 90°. And in case you’re wondering, yes, I did include that restriction in my $Assumptions declaration; but it didn’t help. ↩

Next post Previous post