Next post Previous post

Rolling and pulling

June 22, 2023 at 12:44 PM by Dr. Drang

A few days ago, Steve Mould posted a video about the rolling spool problem. He explains the problem well but not in the traditional engineering way. This problem, or a variation on it, is commonly taught to students in elementary engineering mechanics courses, and it’s taught in a particular way to help the students with concepts that will help them with more practical problems. I want to show you that explanation.

First, you should watch Steve’s video:

In his video, Steve mentions a previous video done by Dianna Cowern (Physics Girl), and you should watch that one, too:

Both Steve and Dianna talk about forces when they’re explaining the movement of the spool, and while you can certainly look at the problem that way, it’s unnecessary. This is fundamentally a kinematics problem, not a kinetics problem, and it’s more useful to think of it as such.

If it’s been a while since you’ve used these similar-sounding words, here’s a refresher:

A kinematics approach to the problem looks like this:

Spool with cord pulled horizontally from bottom

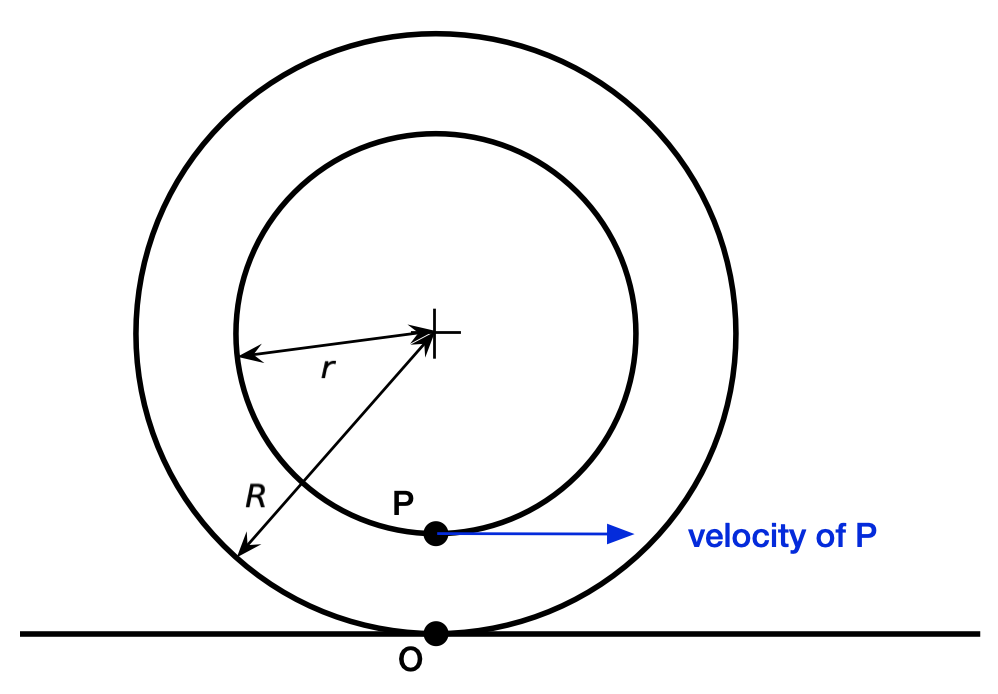
Point O is where the rim of the spool touches the ground; Point P is where the cord plays off the hub. The key feature of this problem is that there is no sliding at either of these points. What that means is that Point O on the spool has the same velocity as Point O on the ground and Point P on the spool has the same velocity as Point P on the cord. Since the ground isn’t moving and the cord is moving horizontally to the right, the velocity of Point O on the spool is zero and the velocity of Point P on the spool is horizontally to the right as shown above. Therefore the spool must be turning clockwise and rolling to the right. We don’t have to think about the tension force in the cord or the friction force at Point O.

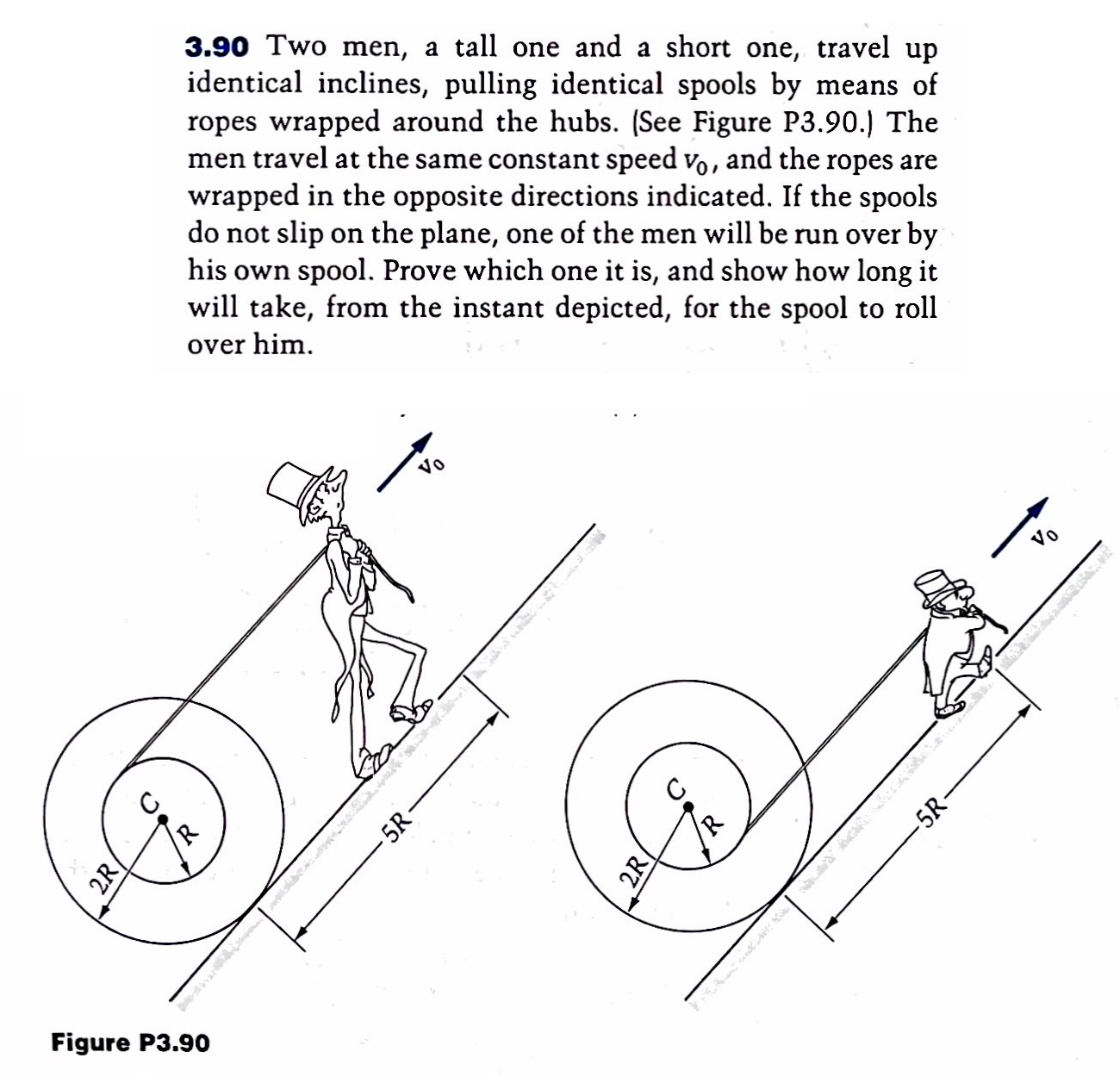
I mentioned above that this problem and variants of it are used to teach how rolling without sliding works. Here’s a cute problem from the second edition (1989) of McGill and King’s Engineering Mechanics: An Introduction to Dynamics:

Rolling problem from McGill and King

And here’s one from the third edition (1941) of Seely and Ensign’s Analytical Mechanics for Engineers:

Rolling problem from Seely and Ensign

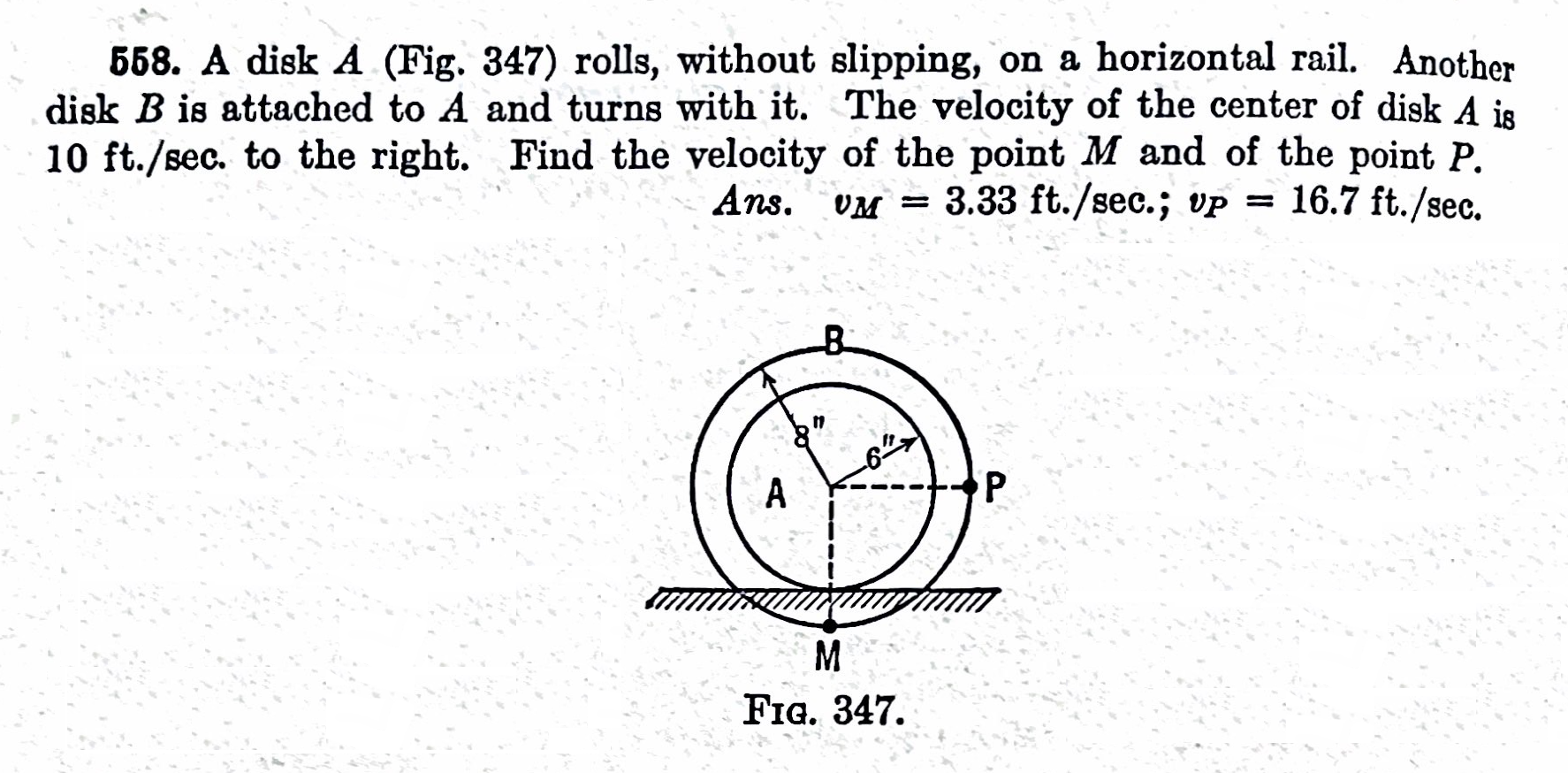
In both problems, the key is to figure out which point has zero velocity, which point has the velocity that’s given in the problem description, and then draw conclusions about all the other points.

Rolling without slipping isn’t just about wheels and spools. The same concept governs the behavior of gears and pulleys, which is why it’s important to teach to mechanical engineering students. And there’s a more general concept, the instantaneous center of rotation, that’s used to simplify the solution all kinds of mechanism problems. These are all fundamentally kinematics problems—you can solve them without any consideration of forces.

I will say that it’s convenient to think about forces in an extension of this problem that Steve looks at later in his video. If you pull on the spool at an increasing angle above horizontal, at some angle the spool will stop rolling to the right and will start rolling to the left. Rather than going through the (fairly simple) math, he kind of waves his hands and briefly flashes this diagram on the screen:

Steve Mould free-body diagram

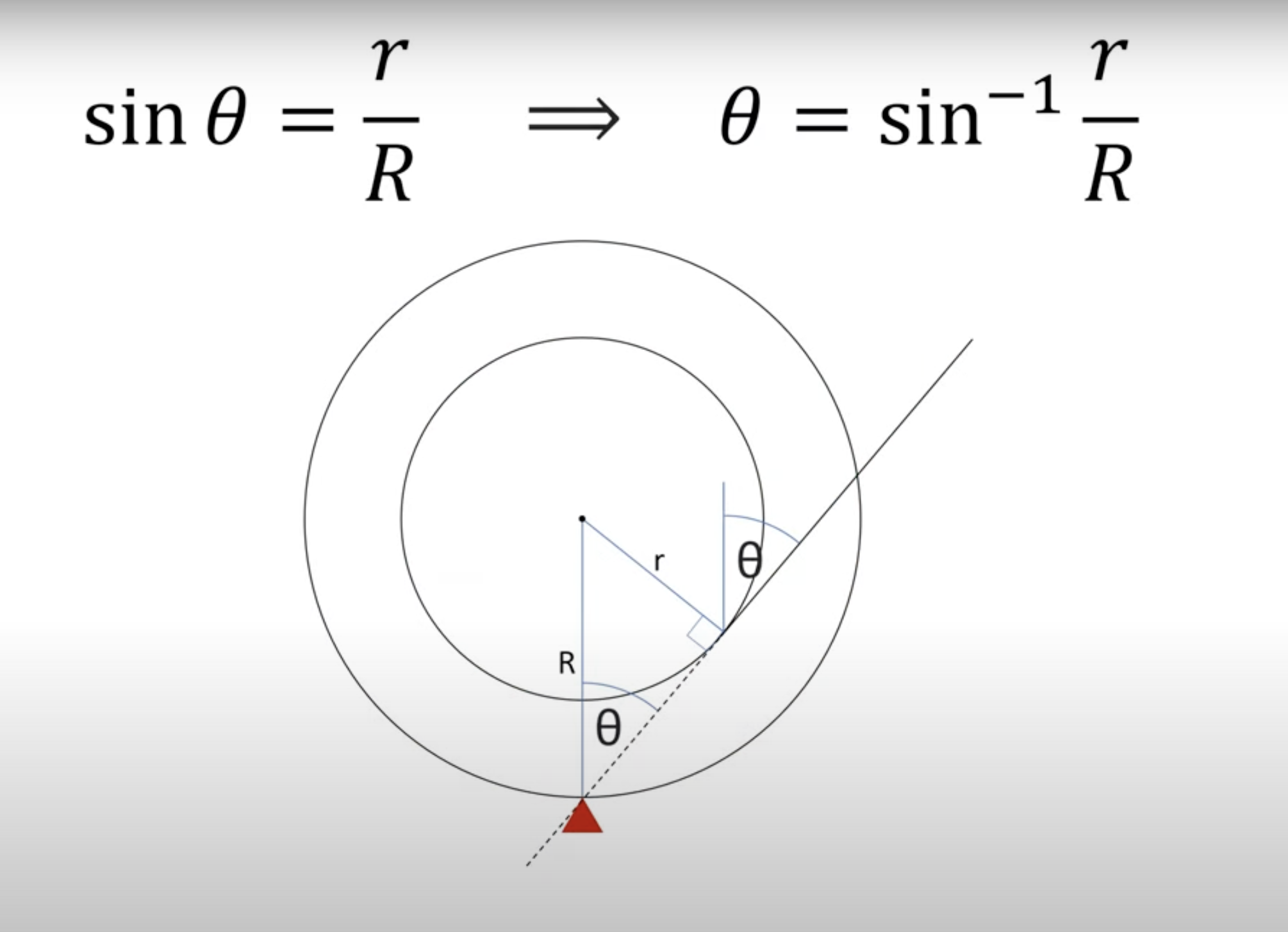
The idea is that when the line of action of the pulling force on the cord reaches the angle shown in the diagram—which means that an extension of the straight portion of the cord would pass through the point of contact between the spool and the ground—there is no tendency to rotate the spool either clockwise or counterclockwise. This is the angle at which the turning direction changes.

But we can get to the same conclusion purely through kinematics. Here’s a diagram of velocities when the angle of the cord is only slightly above horizontal:

Spool with cord pulled at low angle

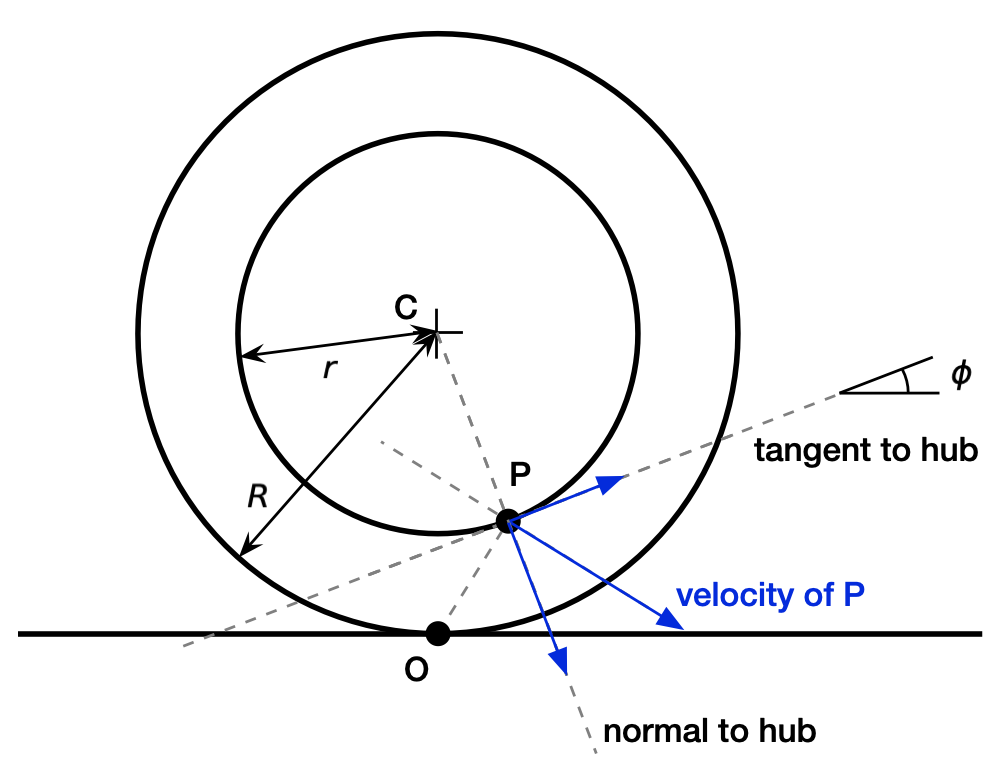
The diagram is kind of messy because we have to look at two sets of lines and their perpendiculars, but the principles behind it are simple.

  1. The velocity of P must be at right angles to the line OP. That’s a fundamental consequence of rolling without slipping.
  2. We can decompose the velocity of P into two perpendicular components, one tangent to the hub and the other normal to the hub. This is how vectors work, and velocity is a vector.
  3. The tangential component of the velocity of P must be in the direction we’re pulling. That’s sort of the definition of pulling.

The first principle says the velocity of P must be either up and to the left or down and to the right. The combination of the second and third principles sets the direction of the tangential component, and the direction of the tangential component sets the direction of the velocity of P. The tangential component must make an acute angle with the resultant, so the velocity of P is down and to the right, as shown.

With the direction of P’s velocity set, we conclude that the spool rolls clockwise for a low pulling angle (this includes the angle of 0°, which was our original problem).

We can go through the same line of reasoning for a high pulling angle:

Spool with cord pulled at high angle

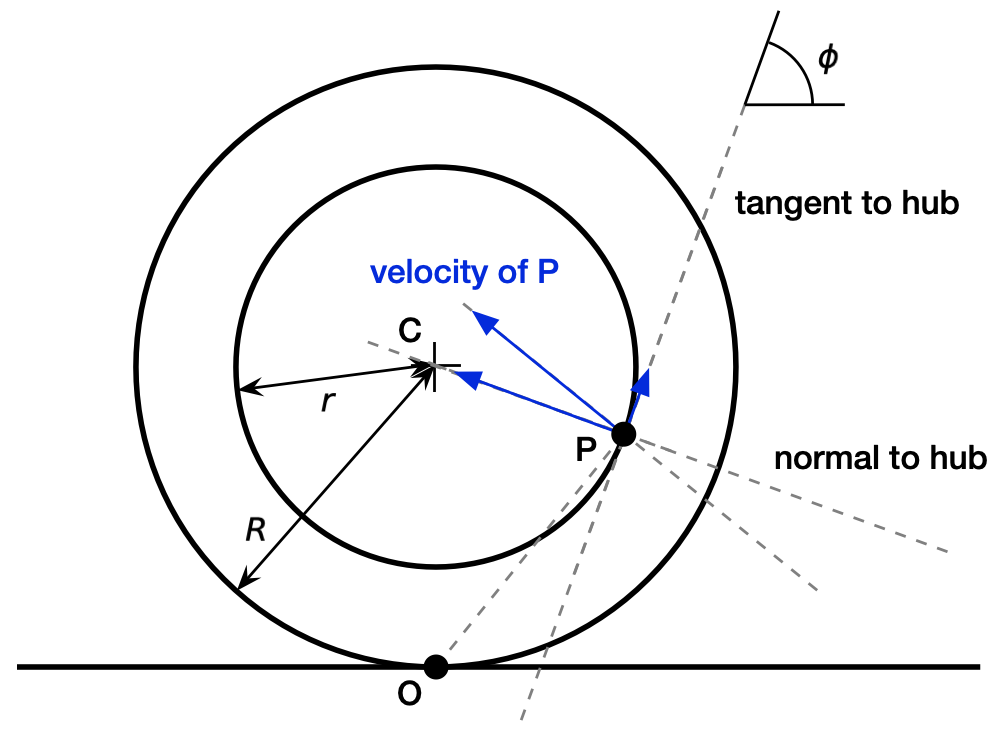
In this case, reasoning from the same principles lead to the conclusion that the velocity of P is up and to the left, which means that the spool rolls counterclockwise for a high pulling angle.

What is the boundary between low and high angles? It’s when the tangential component of the velocity of P is zero. That happens when the line tangent to the hub passes through Point O, and Points O, P, and C make a right triangle.

Right triangle of points

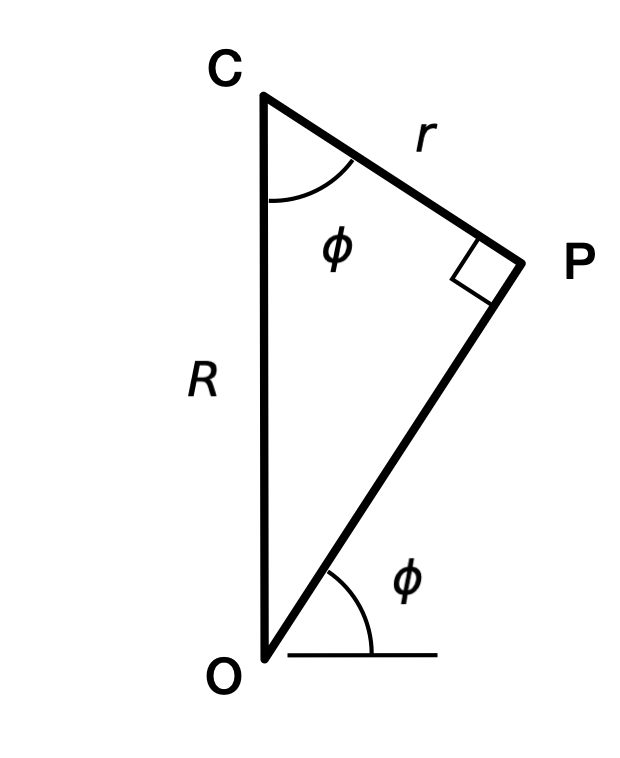
A little trigonometry tells us that’s when

cosϕ=rR\cos \phi = \frac{r}{R}

or

ϕ=cos−1rR\phi = \cos^{-1} \frac{r}{R}

This is the same answer Steve Mould got; his angle θ\theta is the complement of my angle ϕ\phi.

We could have gone straight to this answer, I suppose, but I thought the solution would be clearer if we looked at the low and high angle conditions first.

Going back to the beginning of the post, you’ll note that Steve calls the rolling spool problem a paradox and Dianna calls it a riddle. That’s because most people will think the spool rolls the other way. The goal of engineering education is so thoroughly pound the kinematics into your head that you don’t think of this problem—or any of its relatives—as puzzling at all.

Next post Previous post