The Prime Directive
June 25, 2023 at 10:52 AM by Dr. Drang
I don’t intend for this blog to turn into commentary on YouTube videos, but here’s another one.
If you like math puzzles, the Mind Your Decisions channel from Presh Talwalkar is worth looking into. Unlike many math YouTubers, Presh doesn’t stretch his videos out by going through each step in painful detail. He presents the puzzle, works through a solution that respects your intelligence, and finishes up in about five minutes.
In this recent video, the puzzle concerns prime numbers.
The question is:
There are 168 prime numbers less than 1000. What is their sum?
You’re not expected to work out the sum. It’s a multiple choice problem with four possible answers:
- 11,569
- 76,127
- 57,298
- 81,744
I started the solution the same way Presh did, by noticing that two of the answers were even and two were odd. Since every prime number other than 2 is odd, that means the answer is the sum of 167 odd numbers plus 2. Since the sum of an odd number of odd numbers is an odd number (yes, I enjoyed writing that), the sum we’re looking for must be odd. That eliminates (c) and (d).
At this point, Presh and I took different paths, and when I watched his solution, I felt he had cheated a bit. His reasoning was based on a simple truth: the sum of the first 168 primes must be greater than the sum of the first 168 positive integers, i.e.,
where I’m using to represent the nth prime. This eliminates 11,569 as a possible answer, leaving 76,127.
I don’t object to Presh using Gauss’s trick to simplify the sum of the first 168 integers, but I thought an unwritten rule of this problem was that it was to be done entirely in one’s head. I know there are people who can multiply 168 by 169 more or less instantly, but most of us can’t. So my first instinct was that this was cheating.
Later, I realized the same logic could be used by slipping in a simpler calculation:
We can all do this in our heads because working with computers has gotten us familiar with powers of 2. This also eliminates answer (a).
Anyway, that’s not how I finished the problem. I figured the primes less than 1000 would be nearly uniformly distributed (more on this later) and therefore the average would be about 500. Since
the answer should be close to this. Also, since primes tend to get sparser as they get larger, I would expect the sum to be less than 84,000. That made me feel good about choosing 76,127.
I should have also realized that if 11,569 were the answer, the average of the primes under 1000 would have to be less than 100, which is ridiculous. But I didn’t think of that argument until I started writing this post.
After making my guess and watching Presh’s solution, I opened Mathematica and started playing around. Mathematica has a function, Prime[n], that returns the nth prime number. So
Table[Prime[n], {n, 1, 168}]
gave me the list of the first 168 primes,
2 3 5 7 11 13 17 19
23 29 31 37 41 43 47 53
59 61 67 71 73 79 83 89
97 101 103 107 109 113 127 131
137 139 149 151 157 163 167 173
179 181 191 193 197 199 211 223
227 229 233 239 241 251 257 263
269 271 277 281 283 293 307 311
313 317 331 337 347 349 353 359
367 373 379 383 389 397 401 409
419 421 431 433 439 443 449 457
461 463 467 479 487 491 499 503
509 521 523 541 547 557 563 569
571 577 587 593 599 601 607 613
617 619 631 641 643 647 653 659
661 673 677 683 691 701 709 719
727 733 739 743 751 757 761 769
773 787 797 809 811 821 823 827
829 839 853 857 859 863 877 881
883 887 907 911 919 929 937 941
947 953 967 971 977 983 991 997
and
Sum[Prime[n], {n, 1, 168}]
gave me the answer of 76,127.
As for my assumption that the primes were nearly uniformly distributed, I checked their histogram,
Histogram[Table[Prime[n], {n, 1, 168}], 10]
which gave me this:
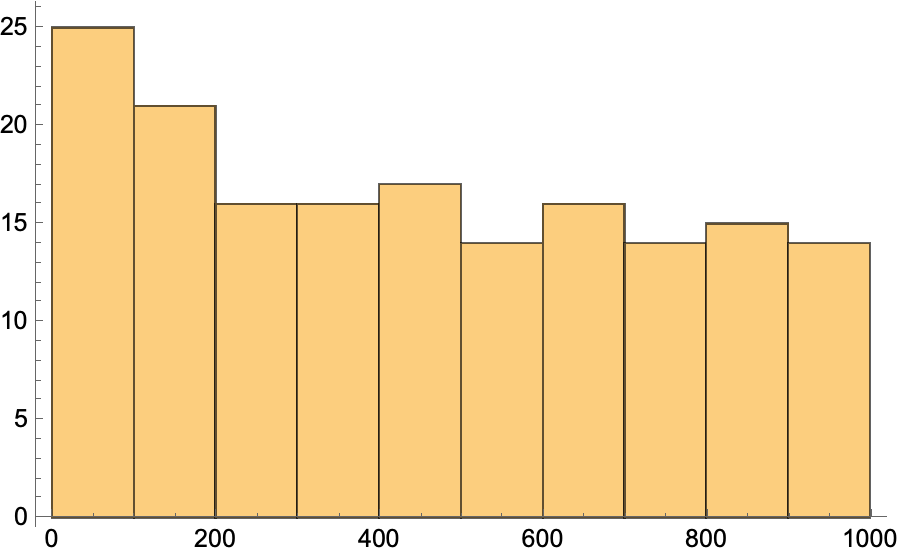
Pretty uniform, except for those under 200. Close enough to uniform for the kind of rough calculation I was doing.

