Next post Previous post

A football score matrix

September 11, 2023 at 6:56 PM by Dr. Drang

John Cook posted a fun article today about the all the possible football scores. The key is to recognize that a team’s score can be any non-negative integer other than one.1 If the most points a team can score is M, then Cook’s reasoning is

Out of the M² pairs of two numbers coming from a set [of] M numbers, M of these pairs are tied, and in half of the rest the first number is higher than the second. So the number of possible scores, with each score bounded by M, is

M + (M² − M)/2 = M(M + 1)/2.

If M = 73 [the most points scored by a team in NFL history], there are 2,701 possible scores.

[Note that there are M possible scores even though 1 is impossible because 0 is possible.]

This is sound logic, but it isn’t how I would solve the problem. My first thought was to arrange the scores in an M×M matrix, with the columns representing the score of the winning (or tying) team and the rows representing the losing (or tying) team. Putting a checkmark at every possible score position and leaving the other positions blank (because the L team can’t score more than the W team), we get an upper triangular matrix:

Matrix of possible scores

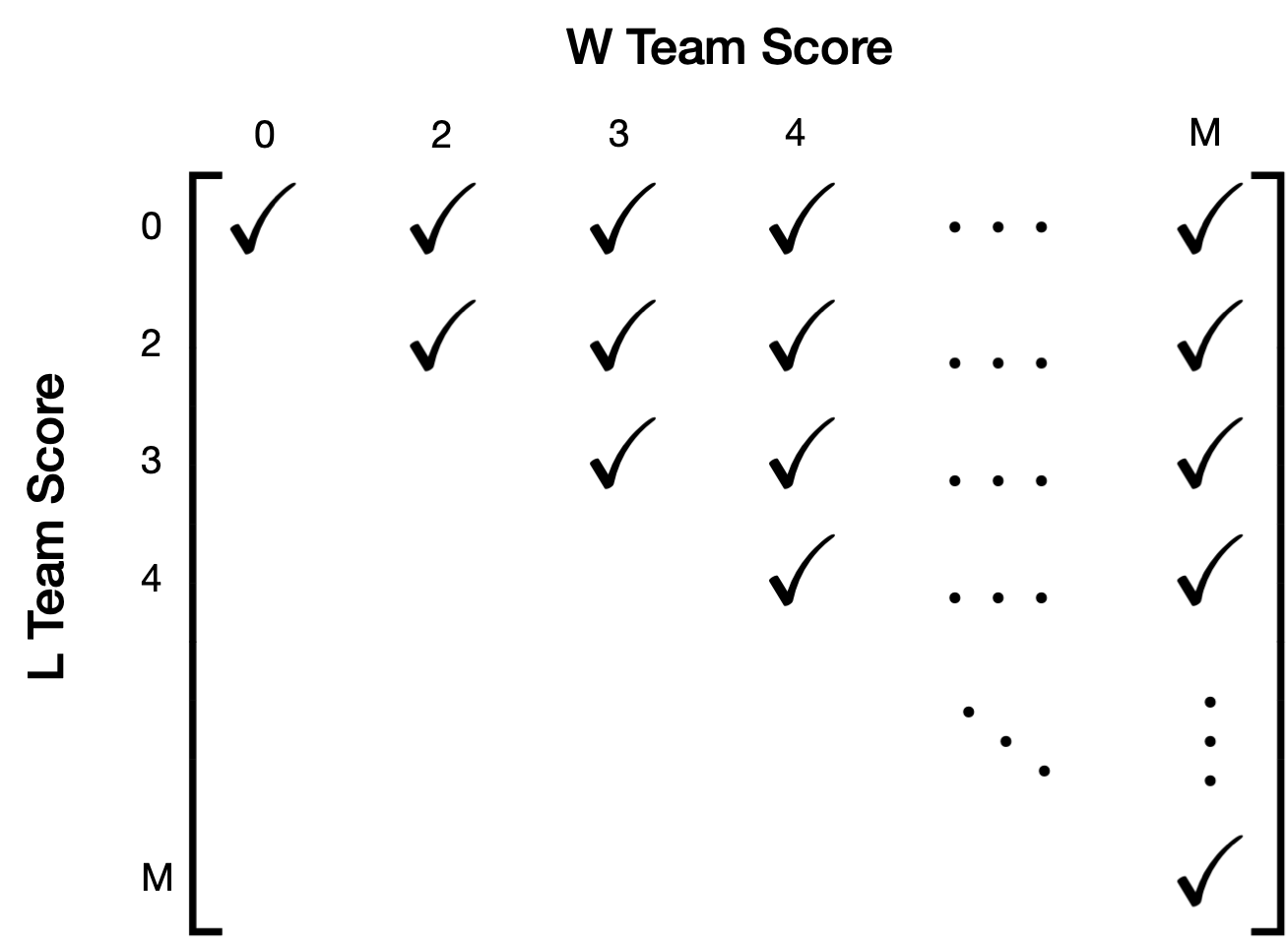
This visual approach came to me because I’ve spent a lot of time dealing with upper (and lower) triangular matrices, and I don’t have to think much to come up with the formula for the number of nonzero terms:

M(M+1)2\frac{M (M + 1)}{2}

You may recognize this as Gauss’s smartass formula for summing the first M natural numbers.

By the way, Cook was inspired to look into this problem by his Texans losing to the Ravens 25–9, a score that, improbably enough, had never happened before.

  1. OK, there is a way for a team to score one point under the one-point safety rule, but we’re going to follow Cook’s argument and ignore that rule. ↩

Next post Previous post