iPhone 15 Pro facts and estimates
September 13, 2023 at 2:40 PM by Dr. Drang
During yesterday’s keynote, I learned some things about the switch from stainless steel to titanium in the iPhone 15 Pro that I’d been guessing about before. I also did some quick and dirty calculations that might explain why Jason Snell thought the 15 Pro seemed distinctly lighter than the 14 Pro, even though the weight reduction is only 9–10%.
The titanium alloy used in the phone was revealed by Isabel Yang about 57 minutes into the presentation. She called it Grade 5 titanium, which is an ASTM designation. It’s also known as Ti-6Al-4V, because its major alloying elements are aluminum at 6% and vanadium at 4%. Allison Sheridan talked about its properties earlier this month, and I’ve been assuming that it would be the alloy Apple would choose ever since I heard they were switching to titanium for the band.
I guessed it would be Ti-6Al-4V because it’s the garden-variety alloy for titanium. A great material, but not exotic in any way. Apart from many aerospace applications, it’s also used in medical implants, so you know that skin contact won’t be a problem.
Shortly after the introduction of the alloy, Yang talked about how the titanium band is attached to the rest of the phone’s structure, which is aluminum. According to Apple’s newsroom:
Using an industry-first thermo-mechanical process, the titanium bands encase a new substructure made from 100 percent recycled aluminum, bonding these two metals with incredible strength through solid-state diffusion.
In other words, the titanium and aluminum are welded together. Not the kind of welding you’re used to, to be sure, but still welding—solid-state welding with no melting of either material. The thermo part of the “thermo-mechanical process” is heating up the materials, and the mechanical part is smushing them together. In essence, this is the oldest form of welding, the kind the village smithy did under the spreading chestnut tree with a forge and a hammer.
I’m sure the process control needed to do solid-state welding with such thin parts is well beyond what other companies can achieve, and I can understand why Apple didn’t want to describe it using a term that conjures up images of sweaty guys in tilt-down helmets making sparks in a dusty manufacturing plant. But it’s still welding.
Finally, we come to Jason Snell’s surprise at how light the 15 Pro seemed when he played with it in the hands-on area. He mentioned this not only in his Macworld article, but also in the post-keynote episode of Upgrade. You wouldn’t expect a change from 206 g for the 14 Pro to 187 g for the 15 Pro would be that noticeable, but Greg Joswiak mentioned it in the keynote and Jason confirmed it. How can that be?
One answer is that people are just more sensitive than we give them credit for being. A 9–10% drop in weight may seem like a small amount to our brains but a large amount to our hands. But because it allowed me to do some simple calculations, I decided to look into another possibility.
Your ability to manipulate a phone is based primarily on its mass, but also on its moment of inertia. And since the reduction in mass when switching from stainless steel to titanium is occurring almost entirely at the perimeter of the phone, the moment of inertia should be reduced more than if the mass were reduced uniformly.
Let’s assume the two phones are the same size1, 147.5 mm high by 71.5 mm wide (the 7.85 mm thickness can be ignored). We’ll set the origin at the geometric center of the phone and the x, y, and z axes will be associated with what would normally be called pitch, roll, and yaw. We’ll be doing enough approximating that there’s no point in trying to account for the phone’s rounded corners.
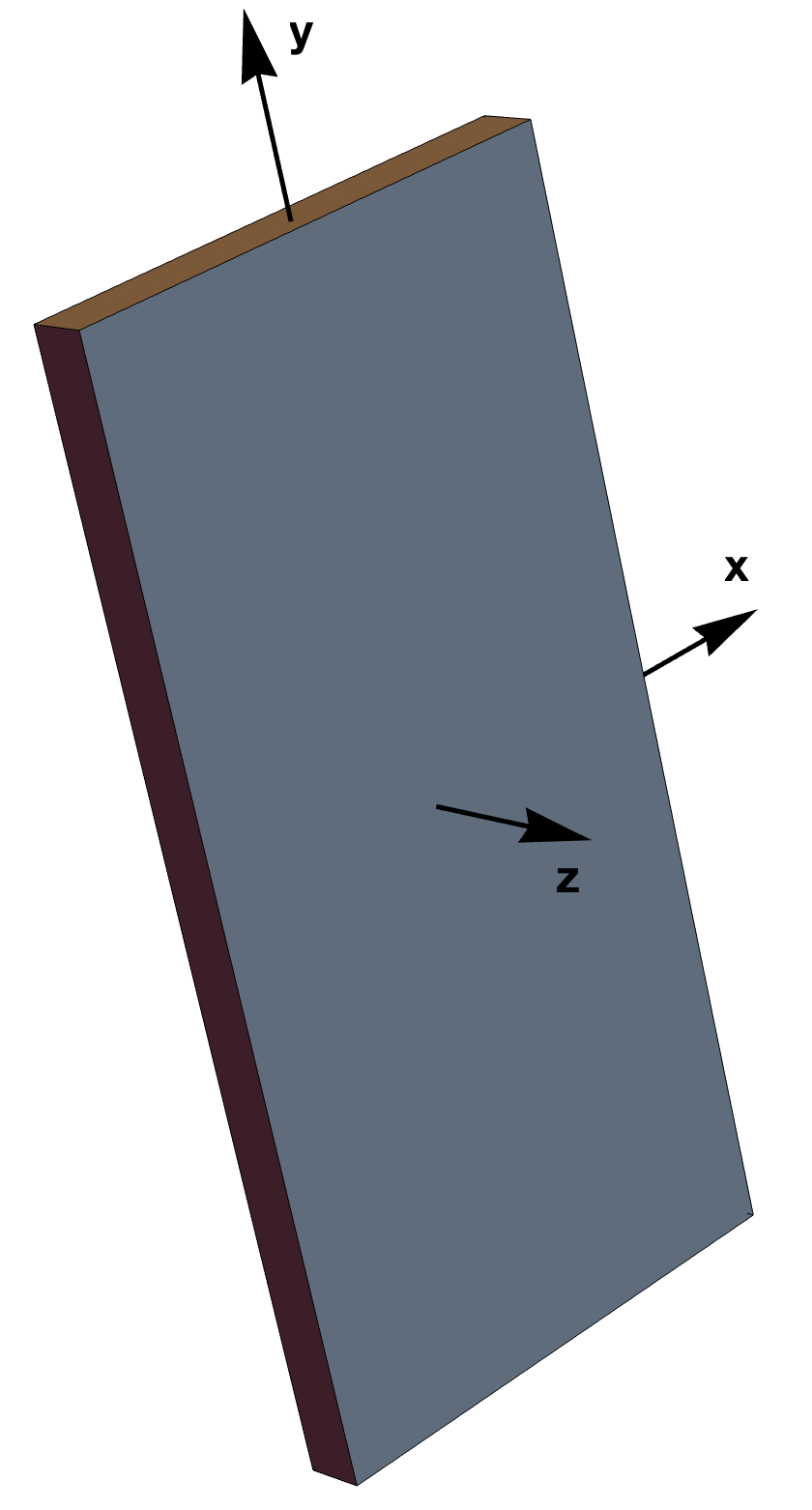
If the 187 g mass of the 15 Pro were distributed uniformly, its moment of inertia about the x-axis would be
If we assume the 14 Pro’s additional 19 g of mass is distributed uniformly around the perimeter, we can say that the long sides have
of extra mass and the short sides have
of extra mass. The moment of inertia of the these four lines of additional mass about the x-axis is
You’ll note the use of the parallel axis theorem in the second term inside the brackets. I’m not calculating the moments of inertia of the top and bottom lines about their own axes because that’s too small to worry about.
Therefore, the moment of inertia of the 14 Pro is
and the reduction in the moment of inertia about the x-axis is
or 14–15%. This reduction, which is more than the mass reduction, would make the iPhone 15 Pro easier to turn, and that may add to the impression that it’s significantly lighter than the 14 Pro.
These calculations were fun, but the initial assumption, that the 15 Pro’s mass is uniformly distributed, is unquestionably wrong. How wrong depends on how non-uniform the mass distribution is, and if I knew that I wouldn’t have had to make the assumption in the first place. My guess is that the assumption is good enough for this kind of back-of-the-envelope calculation.
But even if the numbers are further off than I think, the concept is correct. Reducing the mass at the perimeter, which the change from stainless steel to titanium has done, has definitely reduced the moment of inertia more than a uniform reduction in mass would have. And that will make the 15 Pro easier to manipulate and will contribute—at least somewhat—to the impression of lightness.
You can, of course, do the same sort of calculation for the moments of inertia about the roll and yaw axes. This is left as an exercise for the reader.
-
Yes, I know the 15 Pro is slightly smaller, but I want to follow out the consequences of changing only the mass out at the perimeter. ↩

