And now it’s all this

I just said what I said and it was wrong
Or was taken wrong

Next post Previous post

Ladders and friction

January 11, 2024 at 7:54 AM by Dr. Drang

Rhett Allain, who’s the physics columnist for Wired and a professor of physics at Southeast Louisiana State University, solved a funny problem a couple of weeks ago involving a ladder leaning against a wall. You can see his solution on YouTube or Medium. I think of it as an oddball problem because it’s very different from the “ladder leaning against a wall” problems I’ve been seeing for over 40 years.

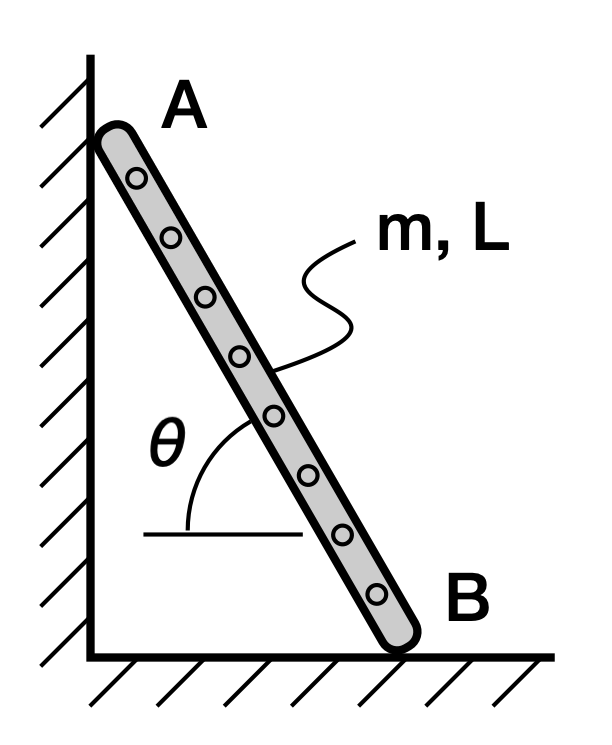
It started as a calculus problem in which you are to assume that Point A moves down the wall with a constant speed and then determine the speed of Point B. Prof. Allain thought (rightly) that Point A of a real ladder wouldn’t fall at a constant speed, so he decided to turn it into a physics problem with gravity acting to accelerate the ladder’s downward movement. His goal in this altered problem was to determine the point at which Point A loses contact with the wall. A key feature in Allain’s problem was zero friction between the wall and the ladder and the floor and the ladder. This certainly makes the solution easier.

Ladder problems in engineering

Both of these problems are different from the ladder/wall problems that are commonly given to engineers in their introductory mechanics courses. Ladders and walls are typically found in the friction section of the study of statics. In these problems, the idea is to determine either

• the lowest angle for which the ladder doesn’t slide down the wall for a given coefficient of friction; or
• the lowest coefficient of friction for which the ladder doesn’t slide down the wall for a given angle.

The key word in these problems is doesn’t. These are statics problems, in which things don’t move, and we look for the conditions under which the ladder stays in place. Here are some images from example problems in textbooks I have:

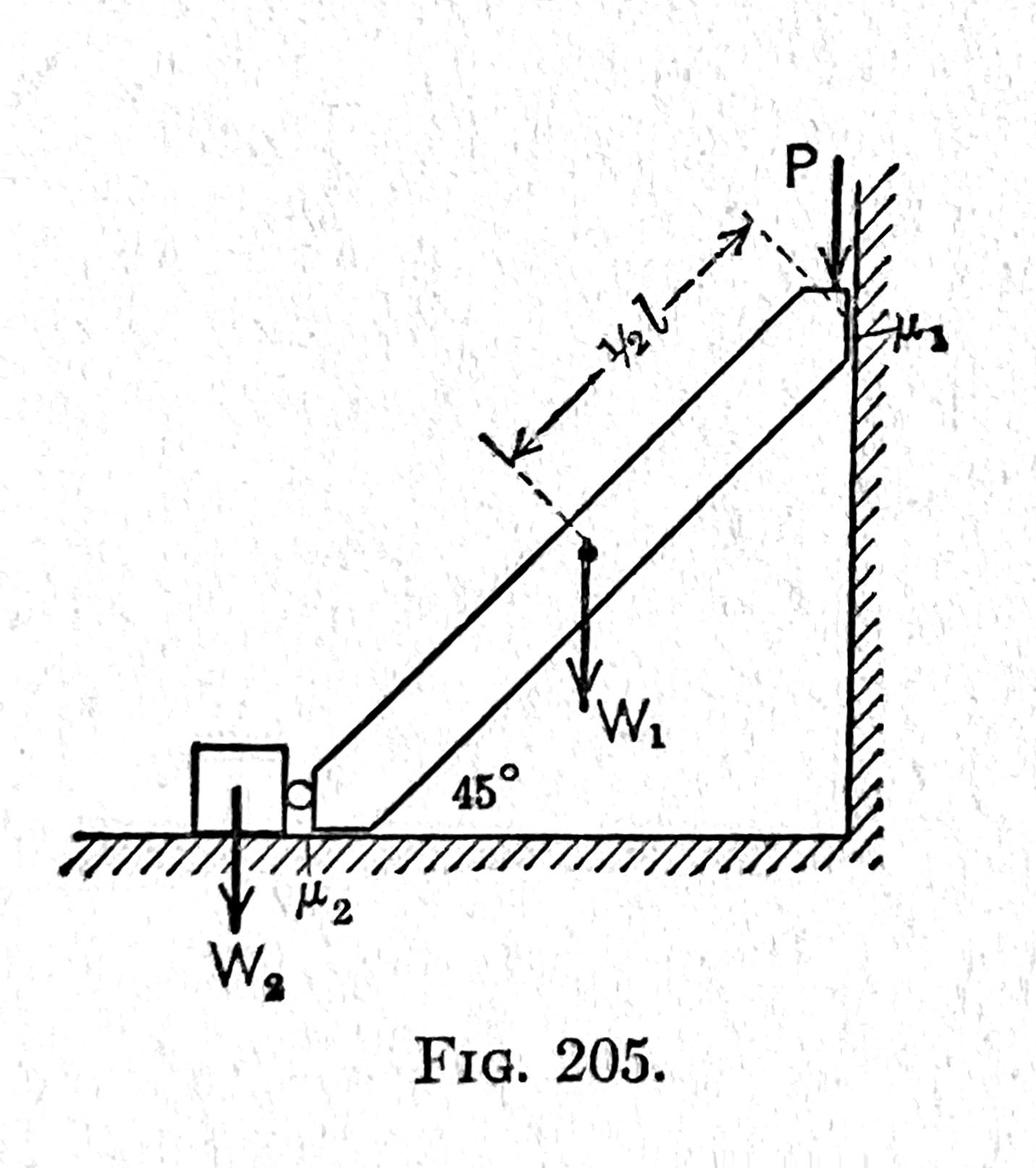
From Seely & Ensign’s Analytical Mechanics for Engineers (Wiley, 1941):

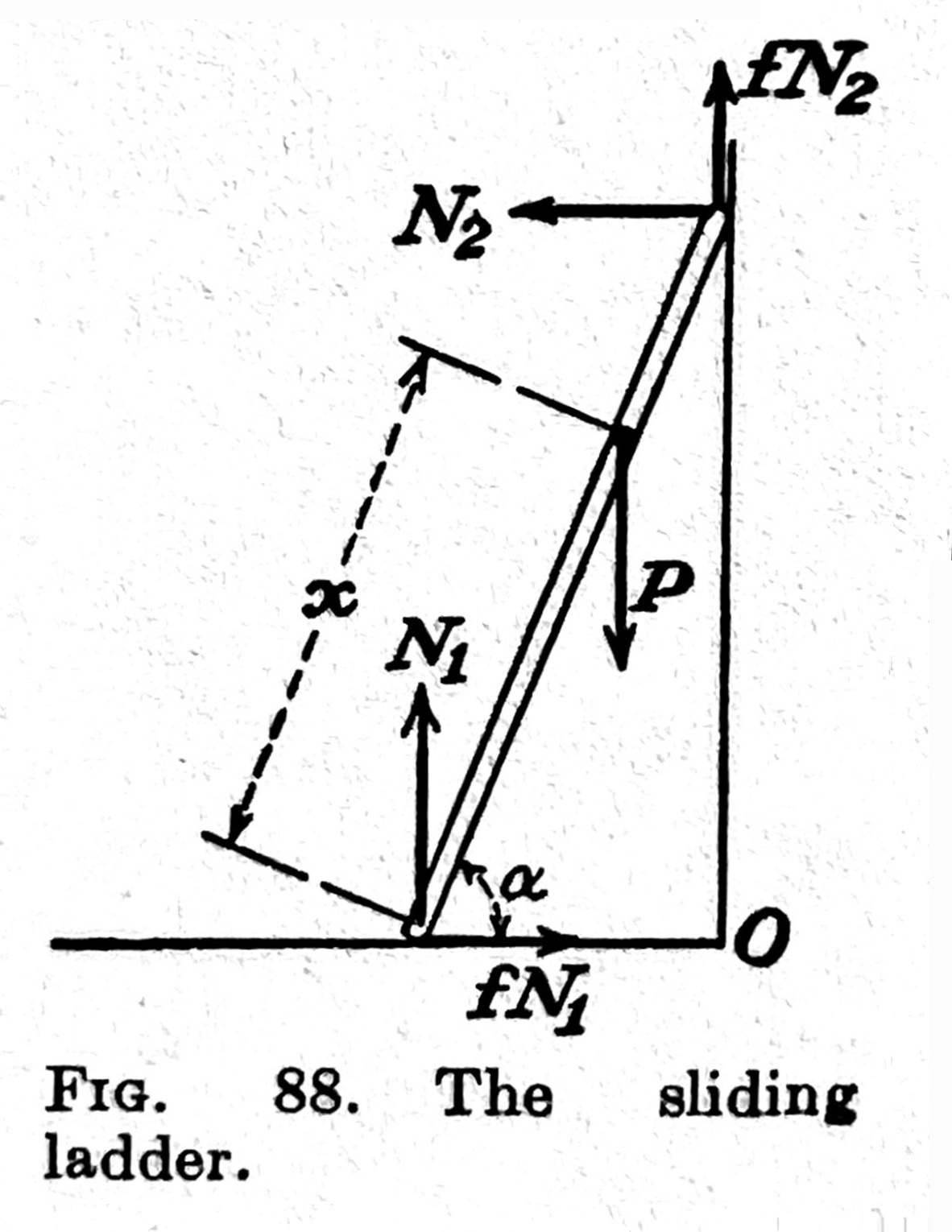
From Den Hartog’s Mechanics (McGraw-Hill, 1948, but I have the Dover reprint):

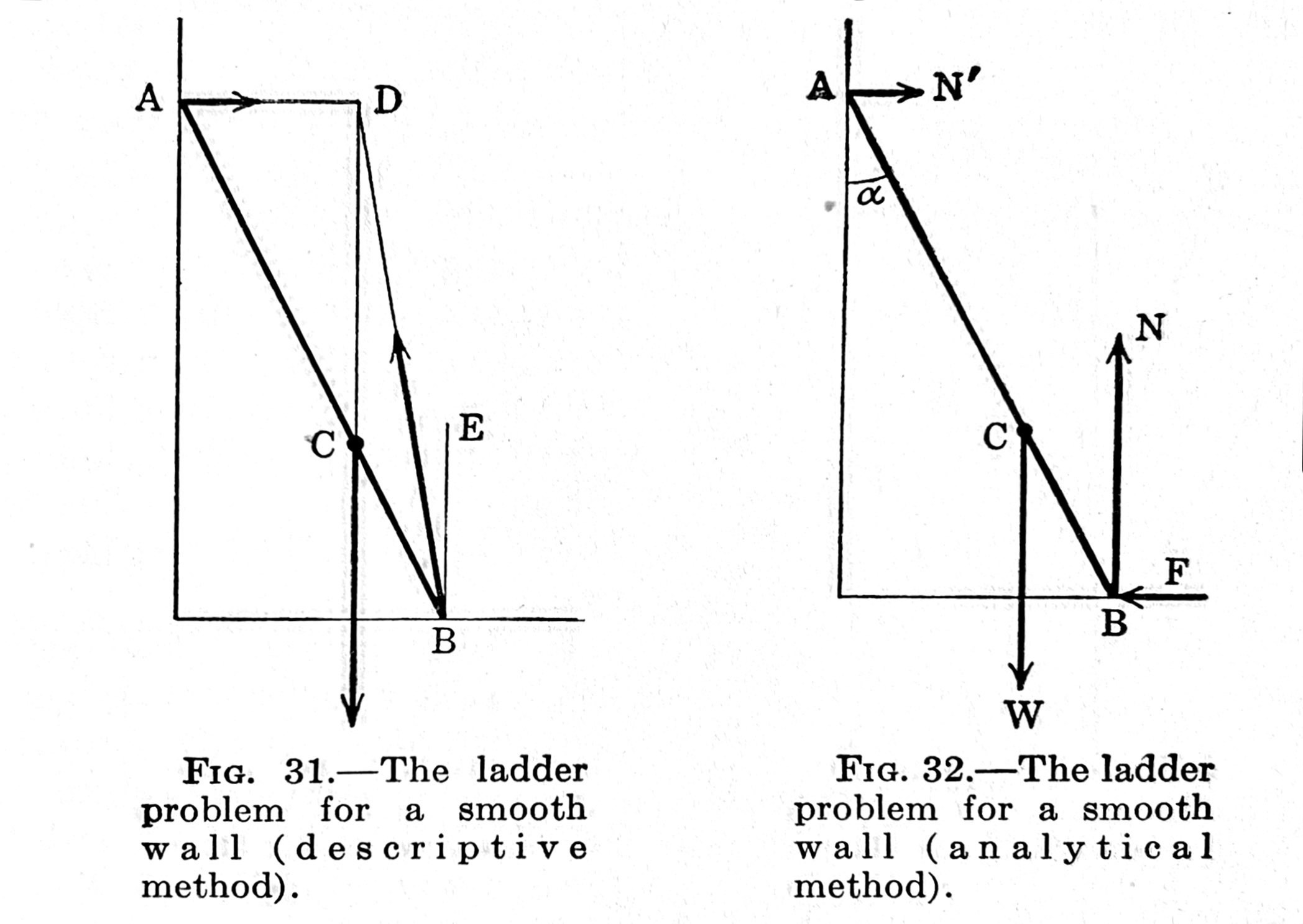
From Synge & Griffith’s Principles of Mechanics (McGraw-Hill, 1949):

From McGill & King’s Engineering Mechanics: Statics (PWS-Kent, 1989):

They use different loading and different friction conditions, but basic idea is the same in all of them.

Static friction

In addition to the laws of statics—Newton’s Second Law with no acceleration—these problems make use of Coulomb’s¹ static friction relationship:

$$f\le \mu N$$

where $f$ is the friction force, which runs parallel to the contact surface in the direction opposite that of impending motion; $N$ is the normal force; and $\mu$ is the friction coefficient. Let’s talk about each of these.

In common speech, “impending” means “about to happen,” but that isn’t quite what the authors of engineering textbooks mean when they use it in this context. These are, after all, statics problems, so there is no movement about to happen. The meaning here has been stretched to “what would happen if there were no friction.”

The “normal” in “normal force” means “perpendicular.” The normal force is perpendicular to the contact surface.

The friction coefficient, $\mu$, is a marvel of engineering simplification. The magnitude of the friction force depends on many things: which two materials are in contact, their surface roughness, any lubrication that might be present, even the temperature. But to get practical solutions, we simplify these many conditions down to a single number. Well, maybe not a single number, because when you look up the friction coefficient for a particular set of materials, you’ll often find a range of values. Still, boiling friction down to a number, even if we don’t know the number exactly, is a great way to think about friction and get reasonable answers.

The simplest ladder problem

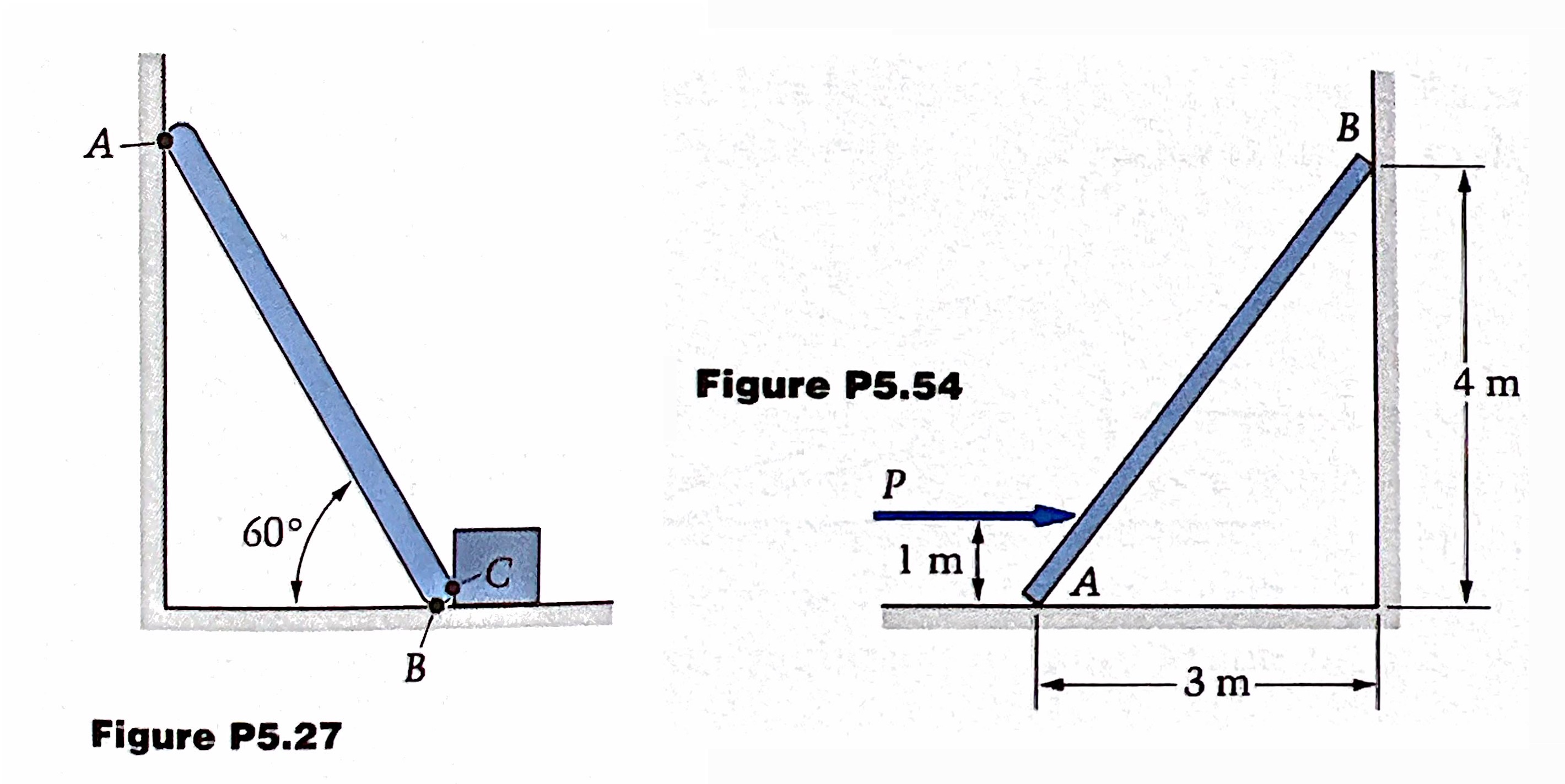
In the simplest version of the ladder problem, we assume there is friction between the ladder and the floor (Point B), but no friction between the ladder and the wall (Point A). If you look carefully, you’ll see that this is the problem Synge & Griffith were exploring. Here’s a free-body diagram of the ladder and all the forces acting on it:

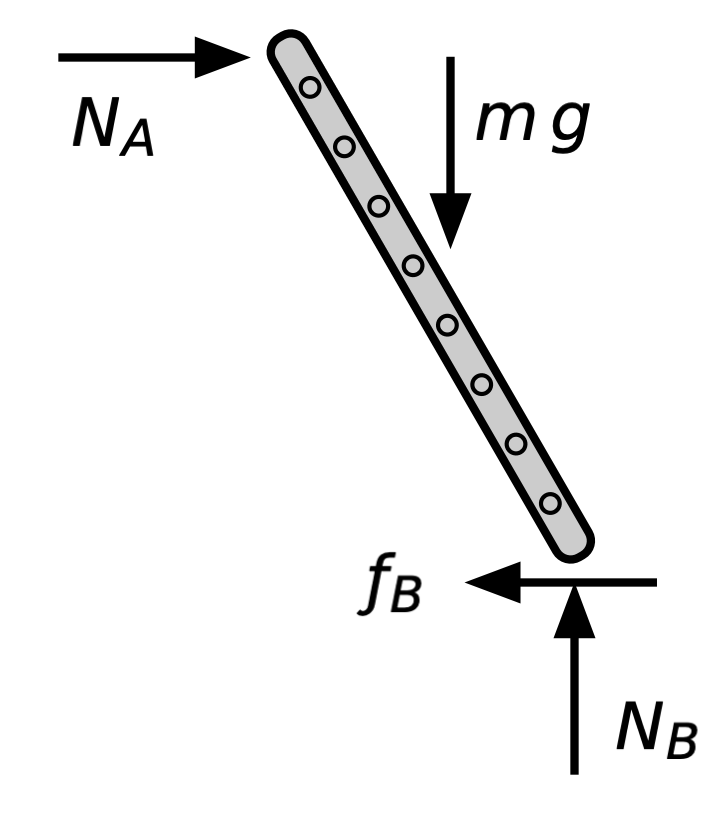
We’ve taken the mass center of the ladder to be at its geometric center.

The three equations of statics are

$$\sum F_x=N_A-f_B=0$$ $$\sum F_y=N_B-\mathrm{mg}=0$$ $$\sum M_B=\mathrm{mg}\left(\frac{L}{2}\cos \theta \right)-N_A(L\sin \theta )=0$$

Here, the x and y directions are horizontal and vertical as usual, and the positive direction for moments about Point B is counterclockwise.

Because we were smart in choosing Point B to take moments about, the second and third equations have only one unknown variable each and can be solved directly:

$$N_B=\mathrm{mg}$$ $$N_A=\frac{\mathrm{mg}}{2}\cot \theta$$

We substitute the second of these solutions into the first statics equation to get

$$f_B=\frac{\mathrm{mg}}{2}\cot \theta$$

Here’s where the friction coefficient comes in. We know that $f_B\le \mu N_B$, so substituting in the solutions from statics, this inequality turns into

$$f_B=\frac{\mathrm{mg}}{2}\cot \theta \le \mu N_B=\mu \mathrm{mg}$$

or, after rearranging,

$$\mu \ge \frac{1}{2}\cot \theta$$

So this gives us the minimum friction coefficient for the ladder to stay up at a given angle. A little algebra tells us the lowest at which the ladder will stay up for a given coefficient of friction:

$$\theta \ge {\tan }^{-1}\frac{1}{2\mu }$$

If you’re worried about trig functions changing signs and messing up these inequalities, recall that the ladder angle is always between 0° and 90°, so there are no sign changes for tangent or cotangent.

A slightly more complicated ladder problem

Now let’s add friction between the ladder and the wall. To keep the number of variables to a minimum, we’ll assume the ladder/wall friction coefficient is the same as the ladder/floor friction coefficient.

Here’s the free-body diagram:

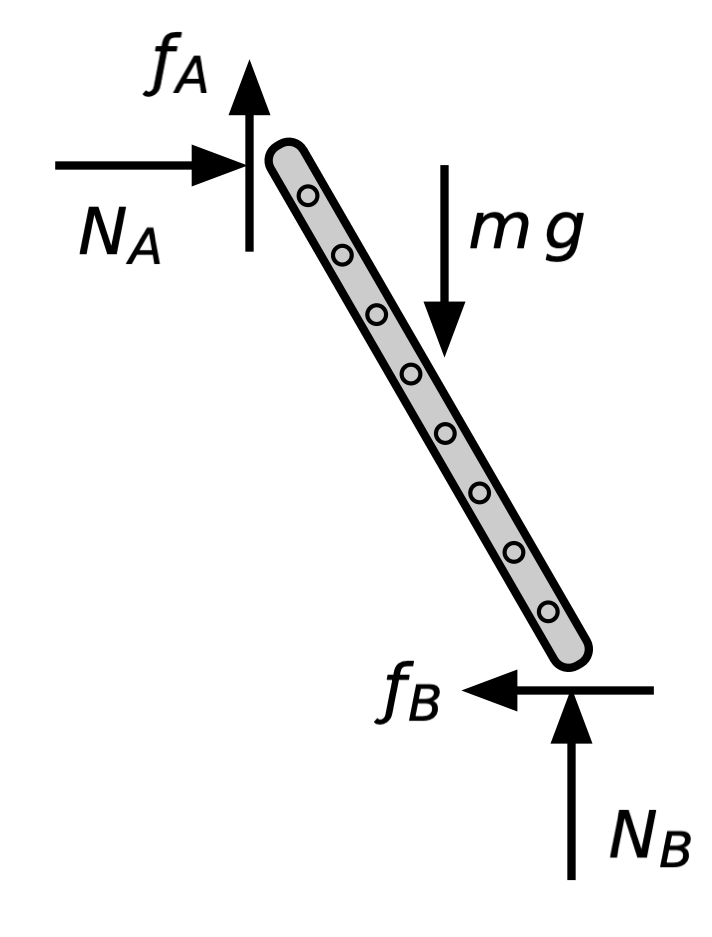
The addition of $f_A$ to the system means we no longer have a statically determinant system. Now we have four unknowns to go with the three equations of statics:

$$\sum F_y=f_A+N_B-\mathrm{mg}=0$$ $$\sum F_x=N_A-f_B=0$$ $$\sum M_B=\mathrm{mg}\left(\frac{L}{2}\cos \theta \right)-N_A(L\sin \theta )-f_A(L\cos \theta )=0$$

And we have two inequalities of Coulomb friction:

$$f_A\le \mu N_A,f_B\le \mu N_B$$

We can combine these five relationships, and if we’re very careful in keeping the inequalities pointed in the right directions, we’ll come up with an inequality that relates the friction coefficient to the angle of the ladder. But most engineers wouldn’t solve the problem that way. Instead, they’d use the following physical reasoning to simplify the algebra:

1. When two surfaces are on the verge of slipping, the inequality in Coulomb’s friction relationship turns into an equality. This makes the algebraic manipulations easier, because we don’t have to worry about the inequality signs flipping on us.
2. The ladder can’t slip at just one of its ends. If it slips at Point A, it must also slip at Point B, and vice versa. And the same is true when the two points are on the verge of slipping.
3. The larger the friction coefficient, the lower the angle at which the ladder will be on the verge of slipping. So when we solve for the ladder angle or friction coefficient on the verge of slipping, it will be the minimum angle or minimum friction coefficient.

Using these three bits of reasoning, we can say

$$f_A=\mu N_A,f_B=\mu N_B$$

and combine these equations with the statics equations as follows:

The second equation of statics tells us that

$$f_B=N_A$$

so

$$N_A=\mu N_B$$

The first equation of statics tells us

$$f_A=\mathrm{mg}-N_B$$

so

$$\mathrm{mg}-N_B=\mu N_A={\mu }^2{N}_B$$

Therefore,

$$N_B=\frac{\mathrm{mg}}{1+{\mu }^2}$$ $$N_A=\frac{\mu \mathrm{mg}}{1+{\mu }^2}$$

and

$$f_A=\frac{{\mu }^2\mathrm{mg}}{1+{\mu }^2}$$

Plugging the expressions for $N_A$ and $f_A$ into the third equation of statics gives

$$\mathrm{mg}\left(\frac{L}{2}\cos \theta \right)-\frac{\mu \mathrm{mg}}{1+{\mu }^2}(L\sin \theta )-\frac{{\mu }^2\mathrm{mg}}{1+{\mu }^2}(L\cos \theta )=0$$

which can be rearranged to

$$(\frac{1}{2}-\frac{{\mu }^2}{1+{\mu }^2})\cos \theta =\frac{\mu }{1+{\mu }^2}\sin \theta$$

This can be simplified in the following steps,

$$\frac{1+{\mu }^2-2{\mu }^2}{2(1+{\mu }^2)}\cos \theta =\frac{\mu }{1+{\mu }^2}\sin \theta$$ $$\frac{1-{\mu }^2}{2}\cos \theta =\mu \sin \theta$$

to

$$\tan \theta =\frac{1-{\mu }^2}{2\mu }$$

So if we’re given $\mu$, the minimum angle for which the ladder won’t slip is

$$\theta ={\tan }^{-1}\left(\frac{1-{\mu }^2}{2\mu }\right)$$

If $\mu >1$, this gives us a negative $\theta$, which is outside the range of ladder angles (0° to 90°) for which the statics equations were written. So a friction coefficient greater than one means the ladder will stay up at any angle.

If we’re given the ladder angle, the minumum friction coefficient to prevent slipping is

$$\mu =\sqrt{1+{\tan }^2\theta }-\tan \theta$$

This one of the two solutions to a quadratic equation. The other gives a negative friction coefficient, which we don’t care about. As the ladder angle approaches 0°, the minimum friction coefficient approaches one. This is consistent with the finding above that a friction coefficient above one means the ladder will stay up at any angle.

Note that our claims that these are the minimum angle and friction coefficient don’t come out of the algebra, they come out of Item 3 of our physical reasoning.

By the way, just because we went through this solution using physical reasoning to simplify the math, that doesn’t mean we couldn’t get the same result using the inequalities and carrying out the algebra. I have a few pages in my notebook in which I did that (including a couple of mistakes along the way) just to prove to myself that I could.

Comparison

One last thing we can do is plot the results of the two problems and see how they compare. Here are the miniumum friction coefficients necessary to keep the ladder from slipping over the full range of angles.

There’s not much difference between the two problems when the ladder angle is high. That’s because the ladder isn’t pressing hard against the wall at those angles, so most of the work of keeping the ladder up in the second problem is being done by the floor/ladder friction. On the other hand, at low ladder angles, the difference between the two problems is huge; the wall/ladder friction in the second problem is doing a lot of work.

Simple problems like this aren’t especially important in the everyday working life of an engineer (unless you work for Werner), but the principles they teach are applicable across many disciplines. That’s why they appear in so many textbooks.

Next post Previous post

Site search

Meta

• drdrang at leancrew
• Blog archive
• RSS feed
• JSON feed
• Mastodon
• GitHub repositories

Recent posts

Credits

This work is licensed under a Creative Commons Attribution-Share Alike 3.0 Unported License.

© 2005–2023, Dr. Drang