Perplexity and beam bending
May 7, 2024 at 10:07 AM by Dr. Drang
David Sparks tested out the Perplexity AI-driven search engine and was moderately impressed, even though he disagreed with one of its answers. I decided to give Perplexity my own test, a structural engineering problem similar to one I gave ChatGPT last year.
My first question was this:
A cantilever beam of length L has a concentrated load P at midspan. What is the deflection at the free end?
This is not the most clearly worded question in the world, but I thought most structural engineers would interpret it as this problem,
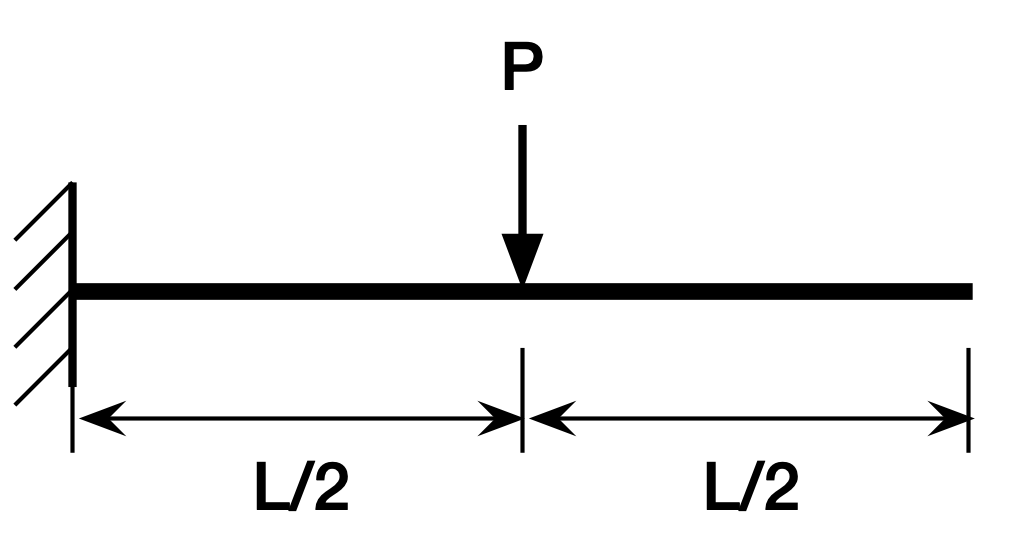
I would have been satisfied if Perplexity had answered “Listen, dumbass, the concept of ‘midspan’ is questionable when it comes to cantilever beams because they don’t have supports at both ends.” Instead, Perplexity gave basically the same wrong answer as ChatGPT did:
For a cantilever beam of length L with a concentrated load P at midspan, the deflection at the free end is given by:
δ_max = PL^3 / (3EI)
Where:
δ_max is the maximum deflection at the free end
P is the concentrated load applied at midspan
L is the length of the cantilever beam
E is the modulus of elasticity of the beam material
I is the moment of inertia of the beam cross-sectionThe key points are:
- The deflection is maximum at the free end of the cantilever beam.
- The deflection varies with the cube of the beam length L, making longer beams much more susceptible to deflection.
- The deflection is inversely proportional to the flexural rigidity EI of the beam, which depends on the material and cross-sectional geometry.
So in summary, to calculate the free end deflection of a cantilever beam with a midspan concentrated load, simply substitute the given values of P, L, E and I into the formula δ_max = PL^3 / (3EI).
Like ChatGPT, Perplexity treated the question as this problem,
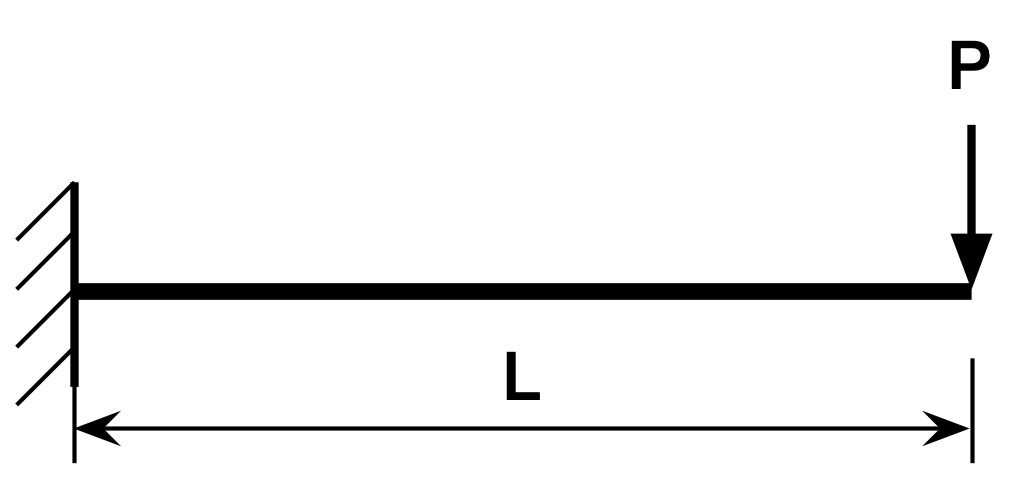
which is perhaps the most common cantilever beam configuration in example problems you’d find on the internet, but it’s not what I asked about.
(Also, “the maximum deflection at the free end” makes less sense than “midspan of a cantilever beam.” But we’ll let that one go.)
I followed up with a clarification and asked Perplexity to try again:
This answer is for the load applied at the free end. I want the deflection at the free end when the load is applied halfway between the fixed end and the free end.
I hoped this was a more explicit description of where the load was applied. Here’s Perplexity’s answer:
For a cantilever beam of length L with a concentrated load P applied at the midspan (L/2 from the fixed end), the deflection at the free end is given by:
δ_max = PL^3 / (8EI)
Where:
δ_max is the maximum deflection at the free end
P is the concentrated load applied at midspan
L is the length of the cantilever beam
E is the modulus of elasticity of the beam material
I is the moment of inertia of the beam cross-sectionThe key points are:
- The maximum deflection occurs at the free end of the cantilever.
- The deflection varies with the cube of the beam length L.
- The deflection is inversely proportional to the flexural rigidity EI.
- For a midspan load, the deflection is 27% higher than for a load at the free end.
So to calculate the free end deflection for a midspan concentrated load on a cantilever beam, substitute the given values of P, L, E and I into the formula: δ_max = PL^3 / (8EI)
It was nice that Perplexity understood where the load was applied and that the formula for deflection had to be different from what it gave me before. However:
The deflection at the free end, as we determined last year, is
not
as Perplexity said.
- The deflection is not “27% higher than for a load at the free end.” Even if we use Perplexity’s answer, one-eighth isn’t 27% higher than one-third. In fact, it’s quite a bit lower (as is the correct answer). So that last bullet point in Perplexity’s answer isn’t just wrong, it’s internally inconsistent.
Every teacher has seen students come up with internally inconsistent answers and not recognize them as such, so in that way Perplexity is mimicking human behavior. But we wouldn’t call it intelligence.

