Floor plans with Python and Shapely
February 16, 2020 at 12:06 PM by Dr. Drang
In yesterday’s post, we outlined portions of a bitmapped floor plan drawing of the the US Capitol, saved the resulting graphic as an SVG file, and used one of Python’s XML libraries to extract the coordinates of the various boundaries. We ended up with seven CSV files, outline.csv, scale.scv, and five files named cutout-01.csv through cutout-05.csv. Today, we’ll use the Shapely library to calculate some properties of the shapes we drew.
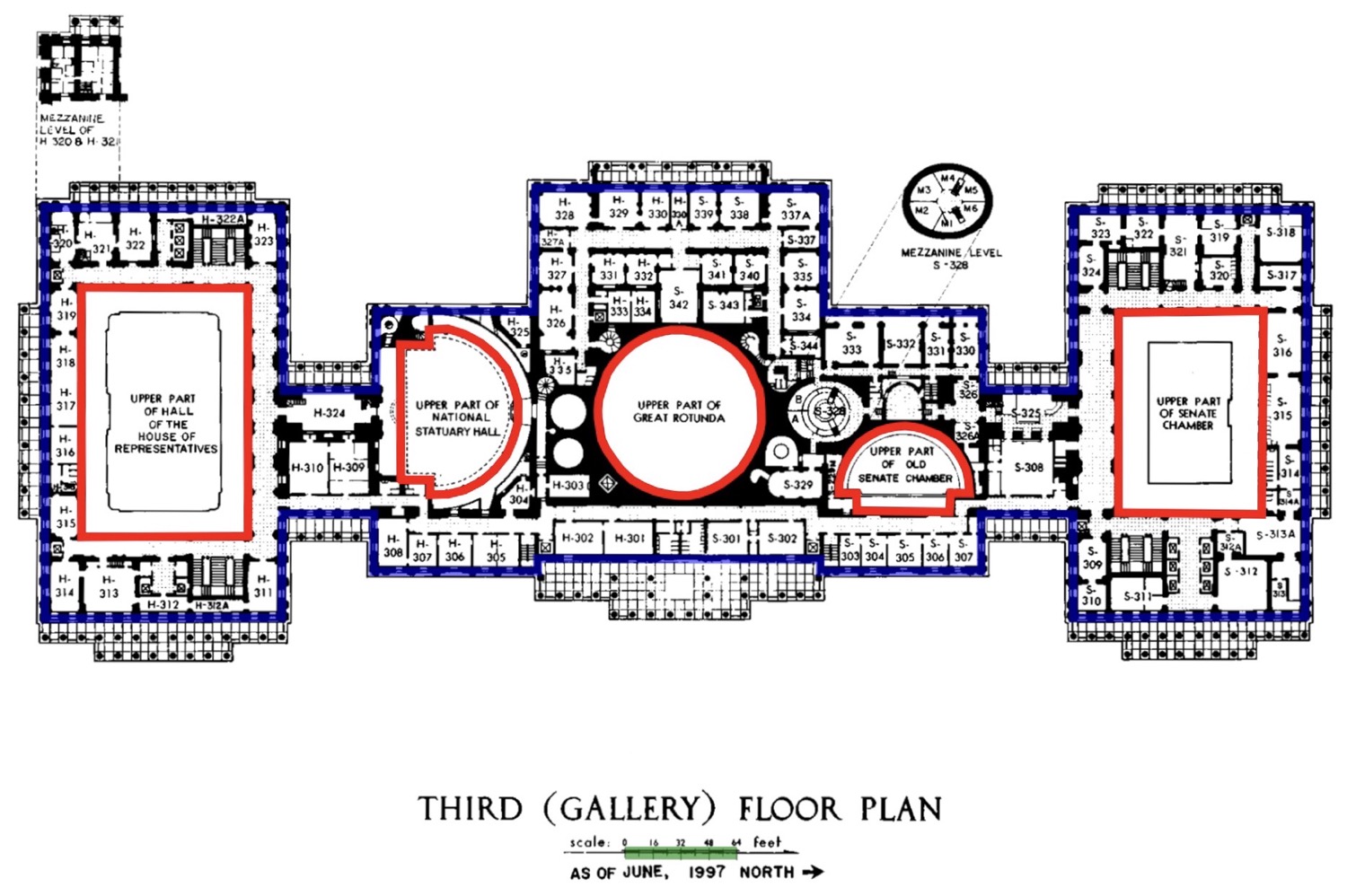
Recall that the blue lines are the overall outline of the building’s third floor interior, the red lines are the outlines of the openings in the third floor that accommodate various multistory rooms in the building, and the green box is set to match the length of the 64-foot scale below the title.
The feature of the Shapely library that does the lion’s share of the calculating for us is the Polygon object, which has some very nice properties for handling real-world shapes. First, it doesn’t require the polygon to be convex, so we can model the reentrant corners that are common in buildings, landscaping, and property boundaries. Second, it allows for holes within the outer shell of the polygon, which is perfect for handling floor openings, atriums, and other items that make shapes multiply connected.
Our goal is to work out the floor area of the third floor. That’s the area enclosed by the outer walls minus the openings. Here’s the code that does it:
python:
1: from shapely.geometry import Polygon
2: import pandas as pd
3:
4: # Work out the scale of the drawing
5: dfscale = pd.read_csv('scale.csv')
6: scale = 64/(dfscale.x.max() - dfscale.x.min())
7:
8: # Get the outline and scale it
9: dfoutline = pd.read_csv('outline.csv')
10: dfoutline.x = dfoutline.x*scale
11: dfoutline.y = dfoutline.y*scale
12:
13: # Do the same for the cutouts
14: dfcutouts = []
15: for i in range(5):
16: dfcutouts.append(pd.read_csv(f'cutout-{i+1:02}.csv'))
17: dfcutouts[i].x = dfcutouts[i].x*scale
18: dfcutouts[i].y = dfcutouts[i].y*scale
19:
20: # Make a polygon without holes
21: ocoords = list(zip(dfoutline.x, dfoutline.y))
22: outline = Polygon(ocoords)
23: print(f'{"Area of outline":>20s}: {outline.area:7,.0f} ft²')
24:
25: # Make a polygon with holes to represent the floor
26: ccoords = []
27: for i in range(5):
28: ccoords.append(list(zip(dfcutouts[i].x, dfcutouts[i].y)))
29: floor = Polygon(ocoords, ccoords)
30: print(f'{"Floor area":>20s}: {floor.area:7,.0f} ft²')
31:
32: # Check all the holes individually
33: holes = ['House Chamber', 'Statuary Hall', 'Great Rotunda', 'Old Senate Chamber', 'Senate Chamber']
34: for i in range(5):
35: hole = Polygon(ccoords[i])
36: print(f'{holes[i]:>20s}: {hole.area:7,.0f} ft²')
And here are the results:
Area of outline: 134,107 ft²
Floor area: 95,848 ft²
House Chamber: 13,493 ft²
Statuary Hall: 5,128 ft²
Great Rotunda: 7,010 ft²
Old Senate Chamber: 2,869 ft²
Senate Chamber: 9,759 ft²
The script starts by using the Pandas library, to read in the CSV files and arrange them in to dataframes. Pandas isn’t really necessary, as the Python standard library has a CSV module, but I’m used to Pandas and I like how quickly you can do calculations on dataframes.
Lines 5 and 6 use the coordinates of the green box saved in scale.csv to calculate the scale of the drawing in feet per pixel. That value, saved in the variable scale, is later used to convert the coordinates of the outline and the cutouts from pixels to feet.
When Lines 9–11 are done, the dfoutline dataframe contains the coordinates in feet of all the vertices of the outer boundary. Similarly, when Lines 14–18 are done, dfcutouts is a list of dataframes with coordinates in feet, one for each of the floor openings.
Now we start using Shapely. Line 21 puts the x and y values of dfoutline into a list of coordinate pairs. Line 22 constructs a Polygon, named outline, from that list, and Line 23 uses the area property to print out the area. This is the gross area enclosed by the boundary. Our next step is to figure out the net area.
Lines 26–28 set up a list of lists of coordinate pairs for all the floor openings. The floor is then defined in Line 29 using a variant on the Polygon constructor that includes holes. This means floor is a multiply connected polygon, and the area property used in Line 30 accounts for the holes.
Note that if all we wanted was the net floor area, we didn’t have to create the outline polygon. I just did that so we could see the difference.
Another unnecessary bit is the set of calculations in Lines 33–36, which tells us the areas of each of the openings. It just lets us check that the sum of the holes is equal to the difference between the outline and floor areas.
While Shapely would be nice if all it did was calculate the areas of irregular shapes, that isn’t all it does. One of the things I use it for is to generate random sampling spots for floor tile, grout, slab concrete, etc. I can generate (x, y) coordinates over the enclosing rectangle of a floor and then use the contains method to filter out those that aren’t within the irregular floor shape of interest. There are also some very helpful set-theoretic functions like intersection, union, and difference, for handling relationships between several shapes.
I should mention that breaking the work into two scripts, one for creating the vertex CSVs and the other for calculating the area, is inefficient. A single script that reads the SVG and puts the vertex coordinates directly into lists would have eliminated all the CSV stuff. But sometimes, especially when you’re first learning the details of a library, it’s nice to have the intermediate steps saved out to files so you can satisfy yourself that things are working the way you expect.
A couple of years ago, I wrote a library for calculating section properties. It does a lot of things that Shapely doesn’t, but it also repeats a lot of what Shapely does and isn’t as versatile in handling input data. On my list of future projects is merging the two, so I can get all the important section properties from a Shapely Polygon.

