Next post Previous post

Triangles and area coordinates

December 15, 2022 at 2:31 PM by Dr. Drang

Earlier this month, John D. Cook posted a nice little article about using a determinant to get the area of a triangle. The method was both familiar and unfamiliar. I knew I’d once learned about getting a triangle’s area from a determinant, but I was sure it wasn’t the same way Cook did it. So I pulled my favorite finite element textbook1 off the shelf to refresh my memory. Now I’m going to inflict that memory on you.

In Cook’s post, he starts with a triangle whose vertices are defined by the three complex variables z 1, z 2, and z 3, where the real part of each variable is the x-coordinate and the imaginary part is the y-coordinate. The area of the triangle can be computed through this non-obvious formula:

A=i4|z 1 z¯ 1 1 z 2 z¯ 2 1 z 3 z¯ 3 1| A = \frac{i}{4} \, \begin{vmatrix} z_1 & \overline{z}_1 & 1 \\\\ z_2 & \overline{z}_2 & 1 \\\\ z_3 & \overline{z}_3 & 1 \end{vmatrix}

where the straight lines on either side of the matrix represent the determinant, and a bar over a variable represents the complex conjugate.

Although this is a compact and easy-to-remember formula, I knew it wasn’t the one I learned back in my finite element analysis class, primarily because we didn’t use complex variables in that class. But we did use area coordinates, and that’s where I learned how to get the area of a triangle from a (different) determinant.

Area coordinates—also called natural coordinates—for triangles are a set of three variables, ξ 1, ξ 2, and ξ 3, that conveniently define a point within a triangle. Given the point P shown below, its coordinates are

ξ 1=A 1A,ξ 2=A 2A,ξ 3=A 3A

where A is the area of the entire triangle, and

A 1+A 2+A 3=A

Area coordinates

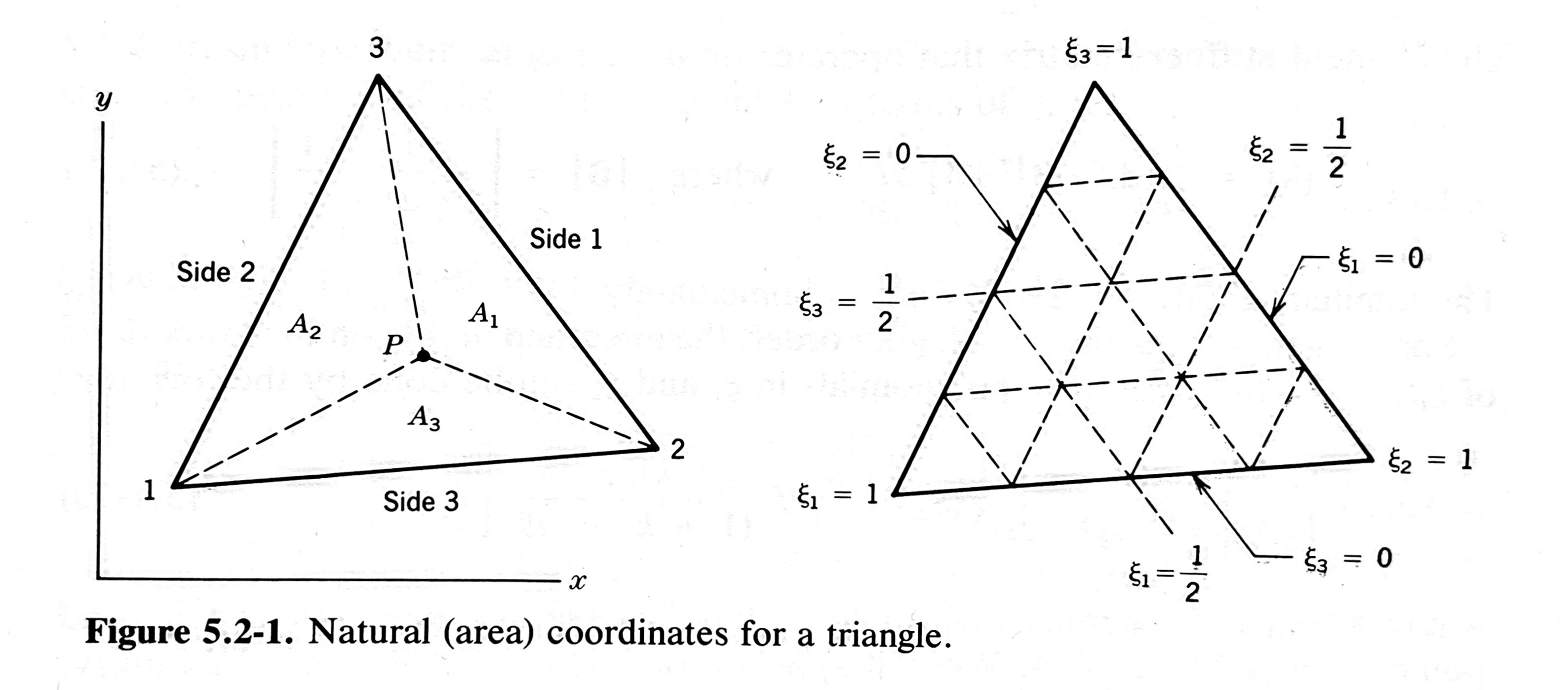
The advantage of using area coordinates is shown in the drawing on the right.2 For each vertex, one of the coordinates is one and the other two are zero. Along each side, one of the coordinates is zero and the other two add to one. Another nicety of area coordinates is that the centroid of the triangle is at (13,13,13).

Of course, using three coordinates to define a point in a plane involves one degree of redundancy. If you know two of the coordinates, the third can always be calculated through

ξ 1+ξ 2+ξ 3=1

which is a direct consequence of the area summation formula above.

If you’re dealing with just one triangle, there’s not much value in using area coordinates. But if you’re doing a finite element analysis with triangular elements, you can easily have thousands of elements, so the consistency of area coordinates can be a big help—if you can easily transform between the xy and area coordinate systems. And you can. Here’s the relationship:

{1 x y}=[1 1 1 x 1 x 2 x 3 y 1 y 2 y 3]{ξ 1 ξ 2 ξ 3}

Note that the top row of the transformation matrix represents the constraint equation among the area coordinates.

The inverse transformation isn’t as nice, but it’s not too bad:

{ξ 1 ξ 2 ξ 3}=12A[x 2y 3−x 3y 2 y 2−y 3 x 3−x 2 x 3y 1−x 1y 3 y 3−y 1 x 1−x 3 x 1y 2−x 2y 1 y 1−y 2 x 2−x 1]{1 x y}

If you remember how matrix inversion works, you may suspect that 2A is the determinant of the original transformation matrix. And you’d be right. Therefore, the area can be calculated through this simple determinant:

A=12|1 1 1 x 1 x 2 x 3 y 1 y 2 y 3| A = \frac{1}{2} \begin{vmatrix} 1 & 1 & 1 \\\\ x_1 & x_2 & x_3 \\\\ y_1 & y_2 & y_3 \end{vmatrix}

It’s as easy to remember as the formula Cook wrote about and easier to compute—no need to carry around two terms for each variable.

It’s not too hard to show that this determinant and Cook’s are equivalent, especially if you have a computer algebra system. Both areas can be reduced to

A=12[ x 1(y 2−y 3)+x 2(y 3−y 1)+x 3(y 1−y 2)]

which takes up less space vertically but isn’t really any simpler than the area coordinates-based determinant form.

  1. Amazon has the fourth and current edition (2001) of the Concepts and Applications of Finite Element Analysis, written by Robert Cook (no relation to John, as far as I know) and various coauthors. It’s still in print after 20 years without a revision, a testament to its value. I have the third edition (1989) and learned from the second edition (1981). ↩

  2. I wish the triangle in the figure, which I scanned from Chapter 5 of Robert Cook’s book, didn’t look so much like an equilateral triangle. Area coordinates can be used on any triangle. ↩

Next post Previous post